LeetCode——1305. 两棵二叉搜索树中的所有元素

给你 root1 和 root2 这两棵二叉搜索树。

请你返回一个列表，其中包含 两棵树 中的所有整数并按 升序 排序。.

示例 1：

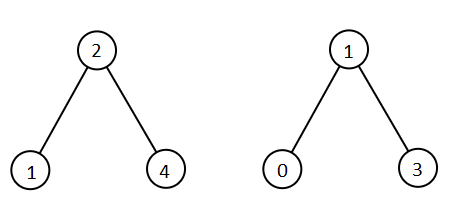
输入：root1 = [2,1,4], root2 = [1,0,3]
输出：[0,1,1,2,3,4]

示例 2：

输入：root1 = [0,-10,10], root2 = [5,1,7,0,2]
输出：[-10,0,0,1,2,5,7,10]

示例 3：

输入：root1 = [], root2 = [5,1,7,0,2]
输出：[0,1,2,5,7]

示例 4：

输入：root1 = [0,-10,10], root2 = []
输出：[-10,0,10]

示例 5：

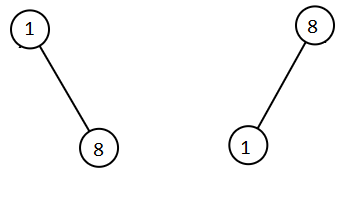
输入：root1 = [1,null,8], root2 = [8,1]
输出：[1,1,8,8]

提示：

每棵树最多有 5000 个节点。

每个节点的值在 [-10^5, 10^5] 之间。

来源：力扣（LeetCode）

链接：https://leetcode-cn.com/problems/all-elements-in-two-binary-search-trees

方法一：遍历 + 排序

我们可以想到的最简单的方法是，对两棵树进行任意形式的遍历（深度优先搜索、广度优先搜索、前序遍历、中序遍历、后序遍历），并将遍历到的所有元素放入一个数组中，最后对这个数组进行排序即可。

C++

class Solution {
public:
    void dfs(TreeNode* node, vector<int>& ans) {
        if (!node) {
            return;
        }
        ans.push_back(node->val);
        dfs(node->left, ans);
        dfs(node->right, ans);
    }

    vector<int> getAllElements(TreeNode* root1, TreeNode* root2) {
        vector<int> ans;
        dfs(root1, ans);
        dfs(root2, ans);
        sort(ans.begin(), ans.end());
        return ans;
    }
};

Python

class Solution:
    def getAllElements(self, root1: TreeNode, root2: TreeNode) -> List[int]:
        ans = list()

        def dfs(node):
            if not node:
                return
            ans.append(node.val)
            dfs(node.left)
            dfs(node.right)

        dfs(root1)
        dfs(root2)
        ans.sort()
        return ans

复杂度分析

时间复杂度：O((M+N)log(M+N))，其中 M 和 N 是两棵树中的节点个数。

空间复杂度：O(H_M + H_N + log(M + N))，其中 H_M 和 H_N是两棵树的高度，这里只计算除了存储答案的数组以外需要的额外空间。上面给出的代码使用深度优先搜索对两棵树进行遍历，需要 O(H_M + H_N)的栈空间；在对数组进行排序时，需要log(M+N) 的栈空间。

方法二：中序遍历 + 归并排序

方法一中并没有用到二叉搜索树本身的性质。如果我们对二叉搜索树进行中序遍历，就可以直接得到树中所有元素升序排序后的结果。因此我们可以对两棵树分别进行中序遍历，得到数组 v1 和 v2，它们分别存放了两棵树中的所有元素，且均已有序。在这之后，我们通过归并排序的方法对 v1 和 v2 进行排序，就可以得到最终的结果。

C++

class Solution {
public:
    void dfs(TreeNode* node, vector<int>& v) {
        if (!node) {
            return;
        }
        dfs(node->left, v);
        v.push_back(node->val);
        dfs(node->right, v);
    }

    vector<int> getAllElements(TreeNode* root1, TreeNode* root2) {
        vector<int> v1, v2;
        dfs(root1, v1);
        dfs(root2, v2);

        vector<int> ans;
        int i = 0, j = 0;
        while (i < v1.size() || j < v2.size()) {
            if (i < v1.size() && (j == v2.size() || v1[i] <= v2[j])) {
                ans.push_back(v1[i++]);
            }
            else {
                ans.push_back(v2[j++]);
            }
        }
        return ans;
    }
};

Python

class Solution:
    def getAllElements(self, root1: TreeNode, root2: TreeNode) -> List[int]:
        def dfs(node, v):
            if not node:
                return
            dfs(node.left, v)
            v.append(node.val)
            dfs(node.right, v)

        v1, v2 = list(), list()
        dfs(root1, v1)
        dfs(root2, v2)
        ans, i, j = list(), 0, 0
        while i < len(v1) or j < len(v2):
            if i < len(v1) and (j == len(v2) or v1[i] <= v2[j]):
                ans.append(v1[i])
                i += 1
            else:
                ans.append(v2[j])
                j += 1
        return ans

复杂度分析

时间复杂度：O(M+N)，其中 M 和 N 是两棵树中的节点个数。中序遍历的时间复杂度为 O(M+N)，归并排序的时间复杂度同样为 O(M+N)。

空间复杂度：O(M+N)。我们需要使用额外的空间存储数组 v1 和 v2。

方法一 前序遍历+排序

先将两棵树的所有节点都放到一个list中，这里可以采用各种类型的遍历（前序、中序、后序、层次）；

然后将list进行排序即可。

Java

public class Problem02 {

    private List<Integer> ansList;

    private void dfs(TreeNode root) {
        if (root == null) {
            return;
        }

        ansList.add(root.val);
        dfs(root.left);
        dfs(root.right);
    }

    public List<Integer> getAllElements(TreeNode root1, TreeNode root2) {
        ansList = new ArrayList<>();
        dfs(root1);
        dfs(root2);
        Collections.sort(ansList);
        return ansList;
    }

}

复杂度分析

时间复杂度：O(nlogn)。因为用到了排序。

空间复杂度：O(n)。开辟了一个m+n(跟n同量级)大小的list，m代表tree1的节点数、n代表tree2的节点数。

方法二 分别中序遍历+归并

前提：这两棵树都是二叉搜索树（BST），而一颗BST中序遍历的结果就是排好序的。

新建两个list，分别对两棵树进行中序遍历得到分别排好序的list1，list2;

已知list1和list2有序，那么将二者归并即可的到一个排好序的总list。（这里时间复杂度也就O(n)）。

public class Problem02_1 {

    private void dfs(TreeNode root, List<Integer> ansList) {
        if (root == null) {
            return;
        }

        dfs(root.left, ansList);
        ansList.add(root.val);
        dfs(root.right, ansList);
    }

    private List<Integer> merge(List<Integer> list1, List<Integer> list2) {
        List<Integer> ansList = new ArrayList<>();
        int size1 = list1.size();
        int size2 = list2.size();
        int index1, index2;
        for (index1 = 0, index2 = 0; index1 < size1 && index2 < size2;) {
            int num1 = list1.get(index1);
            int num2 = list2.get(index2);
            if (num1 < num2) {
                ansList.add(num1);
                index1++;
            } else {
                ansList.add(num2);
                index2++;
            }
        }

        while (index1 < size1) {
            ansList.add(list1.get(index1++));
        }

        while (index2 < size2) {
            ansList.add(list2.get(index2++));
        }

        return ansList;
    }

    public List<Integer> getAllElements(TreeNode root1, TreeNode root2) {
        List<Integer> ansList1 = new ArrayList<>();
        List<Integer> ansList2 = new ArrayList<>();
        dfs(root1, ansList1);
        dfs(root2, ansList2);

        return merge(ansList1, ansList2);
    }
}

复杂度分析

时间复杂度：O(n). 两次的中序遍历和一次的归并操作都是O(n)的时间复杂度。

空间复杂度：O(n).

方法三 遍历+优先队列

在树遍历的时候用一个优先队列（默认小根堆）来添加元素；

然后，将优先队列的元素逐个取出到list中即可。

Java

public class Problem02_2 {

    private PriorityQueue<Integer> priorityQueue;

    private void dfs(TreeNode root) {
        if (root == null) {
            return;
        }

        priorityQueue.offer(root.val);
        dfs(root.left);
        dfs(root.right);
    }

    public List<Integer> getAllElements(TreeNode root1, TreeNode root2) {
        priorityQueue = new PriorityQueue<>();
        dfs(root1);
        dfs(root2);
        List<Integer> ansList = new ArrayList<>();
        while (!priorityQueue.isEmpty()) {
            ansList.add(priorityQueue.poll());
        }
        return ansList;
    }
}

复杂度分析

时间复杂度：O(nlogn)。因为优先队列插入和删除的操作的时间复杂度都是O(logn)，然后有n节点，就是O(nlogn).

空间复杂度：O(n)