ICLR 2018-A Simple Neural Attentive Meta-Learner

Key

时序卷积+注意力机制（前者从过去的经验中收集信息，而后者则精确定位具体的信息。）

解决的主要问题

• 手工设计的限制：最近的许多元学习方法都是大量手工设计的，要么使用专门用于特定应用程序的架构，要么使用硬编码算法（已经内置了特定高级策略的一些方面）组件来约束元学习者解决任务的方式。

---

文章内容

• Introduction

使用传统的监督学习或强化学习方法训练的 artificial learners在只有少量数据可用或需要适应不断变化的任务时通常表现不佳，元学习旨在解决这一缺陷，扩大learner的范围，以分配相关的任务。meta-learner训练是一个相似的任务分配、与目标相关的学习策略,概括了但是看不见的任务从一个类似的任务分配，而不是训练学习者在一个任务。

传统上，一个成功的learner发现了一个在数据点上泛化的规则，而一个成功的meta-learner学习了一个在任务上泛化的算法。

元学习可以形式化为一个sequence-to-sequence的问题，在采用这种观点的现有方法中，瓶颈在于元学习者内化和引用过去经验的能力。

• Meta-Learning Preliminaries

  给定任务T = P(Ti)的分布，元学习者的目标是使其关于θ的期望损失最小化。
  
  

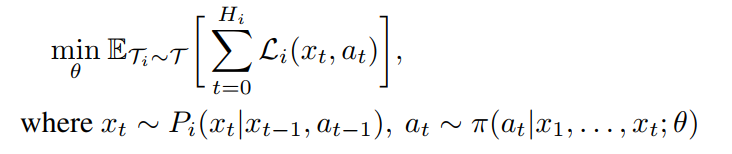
• A Simple Neural Attentive Meta-Learner

  • RNN不足
    
    传统的RNN架构在从一个时间步到下一个时间步的过程中保持信息处于隐藏状态来传播信息，这种时间线性依赖性限制了它们对输入流执行复杂计算的能力

  • TC不足
    
    时间卷积(TC)是因果关系，因此在下一个时间步中生成的值只受过去时间步的影响，而不受未来时间步的影响。与传统的rnn相比，它们提供了对过去信息更直接、高带宽的访问，允许它们在固定大小的时间上下文中执行更复杂的计算。
    
    然而，对于长序列，膨胀率一般呈指数级增长，因此所需层数随序列长度呈对数级增长。因此，他们可以更粗略地访问更早以前的输入;对于元学习者来说，他们有限的容量和位置的依赖是不可取的，元学习者应该能够充分利用越来越多的经验

  • soft attention不足
    
    相比之下，软注意允许模型从潜在的无限大的背景中精确定位特定的信息。它将上下文视为无序的键值存储，可以根据每个元素的内容进行查询。
    
    然而，缺乏位置依赖也可能是不可取的，特别是在强化学习中，在这种学习中，观察、行动和奖励本质上是连续的。

  • SNAIL

    • 结合：
      
      TC以有限的上下文大小为代价提供高带宽访问
      
      soft attention在无限大的上下文上提供精确访问
    • 结构：TC层+attention层+TC层+attention层
      
      它根据当前的观察结果以及之前的观察结果、行动和奖励，输出操作的分布。
      
      
      
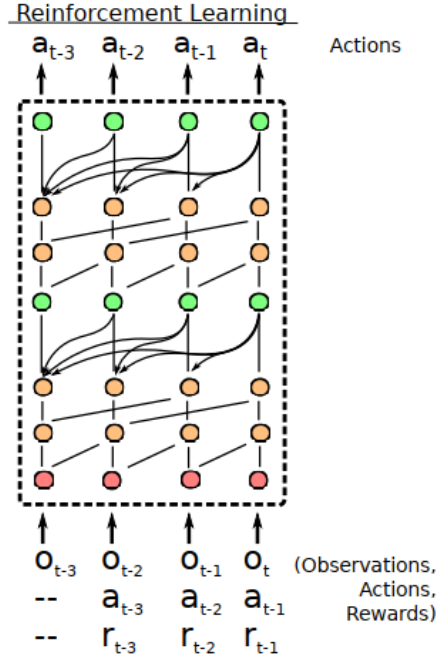
      通过将TC层与因果注意层交错，SNAIL可以在其过去经验的基础上获得高带宽访问，而不会受到有效使用经验量的限制。通过在一个端到端训练的模型的多个阶段使用注意力，SNAIL可以学习从它收集的经验中挑选出哪些信息，以及容易做到这一点的特征表示
    • 网络blocks
      
      composition：A dense block、A TC block、A attention block
      
      【其中A dense block是为了加速深度卷积训练（batch normalization、residual connections、dense connections都可以加速）】

• Experiments

  • 研究问题
    • SNAIL的普遍性如何影响它在一系列元学习任务中的表现?
    • 与专门针对特定任务领域的现有方法相比，它的性能如何，或已经内置了高级策略的元素?
    • SNAIL如何适应高维输入和长期时间依赖关系?
  • 实验设置（与RL2实验相似，并参考了里面数据）
    • 赌博机实验
    • 表格MDPs
    • 可视化航行
    • 连续动作

• Conclusion

简单神经注意学习者(SNAIL)利用了一种新的时间卷积和因果注意的组合，这是两个具有互补优势和弱点的序列对序列模型的构建模块。

未来：终身学习，即训练一个可以在其整个生命周期中都参与的元学习者(而不是像本研究中那样，只在最近几次经历中参与)。具有终身记忆的代理人可以学习得更快，概括得更好;然而，为了保持计算需求的实用性，它还需要学习如何决定哪些经历值得记住。

元学习方法的核心是在性能和普遍性之间进行权衡

---

文章方法的优缺点

• 优点
  • 与传统的rnn(如LSTM或gru)相比，SNAIL更容易训练（RNN：底层的优化可能会很困难，因为存在时间线性的隐藏状态依赖关系）
  • 有效地实现整个序列可以在单个向前传递中处理
• 缺点
  • 基于上下文的，RL中在处理的时候需要一个完整episode

---

Summary

 这篇论文对RNN的长期依赖性提出了两点解决方法：TC时序卷积（允许访问更久之前的信息），注意力机制（弥补TC有限容量的问题，进行键值访问，精确定位特定的信息）。相对于前几次论文中，SNAIL着重解决于网络架构问题，通过网络架构的优化来提高学习效率。

【疑问】但是如果访问之前更久的信息，会不会增大计算量以及时间？Meta-learner是否能够充分的利用之前更久的信息？如果相对于更久信息和较近信息内部特征相似时，learner该如何取舍？

论文链接

版权归原作者 Lee_ing 所有

未经原作者允许不得转载本文内容，否则将视为侵权；转载或者引用本文内容请注明来源及原作者；