2023 ICPC网络赛第一场(A,D,J,L)

2023 ICPC网络赛第一场(A,D,J,L)

A Qualifiers Ranking Rules

先把两场比赛的学校排名处理出来,然后两场比赛的同位次进行合并即可

#include <bits/stdc++.h>

using namespace std;
using i64 = long long;

int main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);

	int n, m;
	cin >> n >> m;
	vector<string> str1, str2,ans;
	map<string, bool> vis1, vis2, vis;
	string s;

	for (int i = 0; i < n; i ++) {
		cin >> s;
		if (vis1[s]) continue;
		str1.emplace_back(s);
		vis1[s] = true;
	}
	for (int i = 0; i < m; i ++) {
		cin >> s;
		if (vis2[s]) continue;
		str2.emplace_back(s);
		vis2[s] = true;
	}

	n = str1.size(), m = str2.size();
	for (int i = 0; i < max(n,m); i ++) {
		if (i < n && !vis[str1[i]]) {
			ans.emplace_back(str1[i]);
			vis[str1[i]] = true;
		}
		if (i < m && !vis[str2[i]]) {
			ans.emplace_back(str2[i]);
			vis[str2[i]] = true;
		}
	}

	for (auto i : ans)
		cout << i << '\n';

	return 0;
}

D Transitivity

如果题目给的所有的团都是完全图,那么就要合并两个最小的团,答案就是这两个团的点数的乘积,否则就要把所有的团都补成完全图,bfs或者并查集即可

#include <bits/stdc++.h>
#define debug(a) cout<<#a<<"="<<a<<'\n';

using namespace std;
using i64 = long long;

typedef pair<i64, i64> PII;

int main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);

	int n, m;
	cin >> n >> m;
	vector g(n + 1, vector<int>());
	for (int i = 0, x, y; i < m; i ++) {
		cin >> x >> y;
		g[x].push_back(y);
		g[y].push_back(x);
	}

	vector<bool> vis(n + 1);
	vector<i64> ans;

	auto bfs = [&](int i) -> pair<i64, i64> {
		queue<int> Q;
		Q.push(i);
		int edge = 0, node = 0;
		while (Q.size()) {
			auto v = Q.front();
			Q.pop();	

			if(vis[v]) continue;
			vis[v] = true;
			node ++;

			for (auto i : g[v]) {
				if (vis[i]) continue;
				Q.push(i);
				edge ++;
			}
		}

		return {node, edge};
	};

	bool is_Tuan = true;
	i64 res = 0;
	for (int i = 1; i <= n; i ++) {
		if (vis[i]) continue;
		auto [num, Edge] = bfs(i);
		if (Edge != num * (num - 1) / 2) {
			is_Tuan = false;
			res += num * (num - 1) / 2 - Edge;
		}
		ans.push_back(num);
	}

	if (!is_Tuan) {
		cout << res << '\n';
	} else {
		sort(ans.begin(), ans.end());
		cout << ans[0] * ans[1] << '\n';
	}

	return 0;
}

J Minimum Manhattan Distance

题意是求在\(C_2\)上取一点到\(C_1\)任意一点的最小期望曼哈顿距离.

由于题目要求是最小期望曼哈顿距离,所以可以等价于看做就到\(C_1\)圆心,为了方便计算,可以把\(C_2\)的圆心看成坐标轴原点,\(C_1\)的圆心通过对称变换到第一象限,设\(\{x_0,y_0\}\)为答案点,则有\(\begin{cases} x_0 = x_2 + r_2\cos\theta \\ y_0 = y_2+r_2\sin \theta\end{cases}\),答案为\(|x_1-x_0|+|y_1-y_0|\),

且题目规定\(\forall x_i \in C_1 \neq \forall x_j \in C_2,\forall y_i \in C_1 \neq \forall y_j\in C_2,\),所以当\(C_1\)在第一象限时,总有\(x_1>x_0,y_1>y_0\),所以绝对值可拆,然后用三角函数计算一下,可得出当\(\theta = \frac{\pi}{4}\)时有最小值\(x+y-\sqrt{2}\times r_2\).

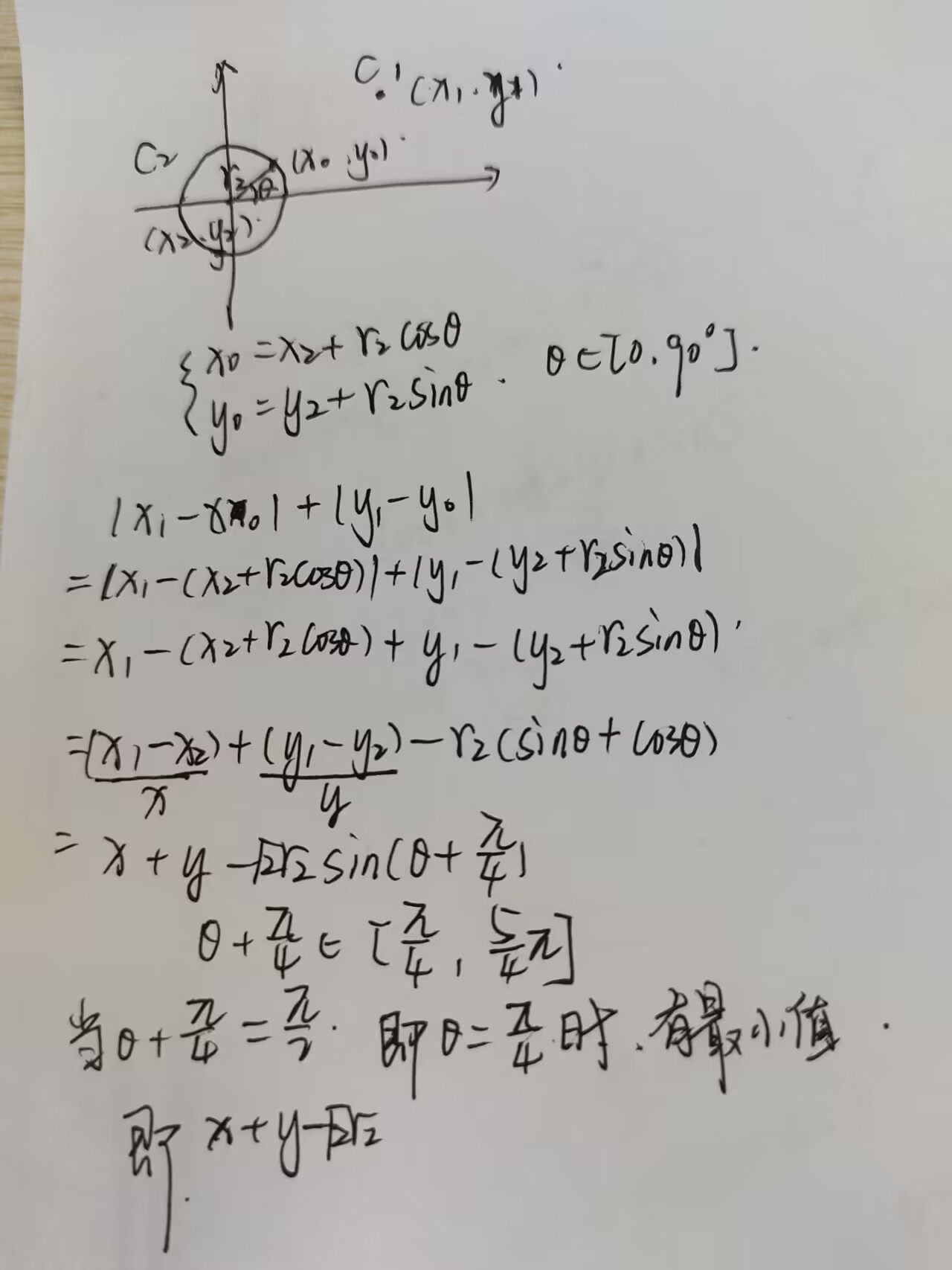
#include<bits/stdc++.h>

using i64 = long long;

using namespace std;

typedef pair<i64, i64> PII;

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    auto get = [&](double x1,double y1,double x2,double y2){
        return sqrt((x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2));
    };

    int T;
    cin >> T;
    while(T--){
        double xa,ya,xb,yb,xc,yc,xd,yd;
        cin >> xa >> ya >> xb >> yb >> xc >> yc >> xd >> yd;
        double r2 = get(xc,yc,xd,yd) / 2;
        double x1 = (xa + xb) / 2, y1 = (ya + yb) / 2;
        double x2 = (xc + xd) / 2, y2 = (yc + yd) / 2;
        double ans = fabs(x1 - x2) + fabs(y1 - y2) - r2 * sqrt(2) ;
        printf("%.10lf\n",ans);
    }

    return 0;
}

L KaChang!

签到题,题目规定了\(k\geq 2\),所以答案为\(\max(2,\lceil\frac{T}{\max\limits_{i=1}^{n}a_i}\rceil)\)

#include <bits/stdc++.h>
#define debug(a) cout<<#a<<"="<<a<<'\n';

using namespace std;
using i64 = long long;

typedef pair<i64, i64> PII;

int main(){
	ios::sync_with_stdio(false);
	cin.tie(nullptr);

	i64 n, k;
	cin >> n >> k;
	i64 ma = 0, x;
	for(int i = 0;i < n;i ++){
		cin >> x;
		ma = max(ma, x);
	}

	cout << max(2ll, (k + ma - 1) / k) << '\n';

	return 0;
}