HDU 5985 Lucky Coins（概率）

http://acm.split.hdu.edu.cn/showproblem.php?pid=5985

题意：
有多种类型的硬币，每种类型的硬币都有一定的数量，现在每次抛硬币，除去朝下的硬币，知道最后只剩下一个硬币或者没有硬币，最后的硬币便是幸运硬币，求每种类型硬币成为幸运硬币的概率。

思路：

硬币的概率都是单独的，所以我们只需要计算一个硬币的概率情况即可。

设die[i][k]表示第i种硬币在第k次全部被抛弃的概率，易得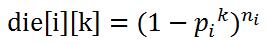，用alive[i][k]表示第i种硬币在第k次至少有一个存活的概率就是$1-die[i][k]$。

最后计算就比较简单了，。

这里k取100就已经足够了，因为100次方已经几乎是0了。

 #include<iostream>
 #include<algorithm>
 #include<cstring>
 #include<cstdio>
 #include<vector>
 #include<stack>
 #include<queue>
 #include<cmath>
 #include<map>
 #include<set>
 using namespace std;
 typedef long long ll;
 typedef pair<int,int> pll;
 const int INF = 0x3f3f3f3f;
 const int maxn = +;

 int n,m,num;
 double p;
 double die[][],alive[][];

 int main()
 {
     freopen("in.txt","r",stdin);
     int T;
     scanf("%d",&T);
     while(T--)
     {
         scanf("%d",&n);
         for(int i=;i<=n;i++)
         {
             scanf("%d%lf",&num,&p);
             for(int k=;k<=;k++)
             {
                 die[i][k]=pow(1.0-pow(p,k*1.0),num*1.0);
                 alive[i][k]=1.0-die[i][k];
             }
         }
         if(n==)  {puts("1.000000");continue;}

         for(int i=;i<=n;i++)
         {
             double ans=;
             for(int k=;k<=;k++)
             {
                 double tmp=;
                 for(int j=;j<=n;j++)
                 {
                     if(i!=j)   tmp*=die[j][k];
                 }
                 ans+=(alive[i][k]-alive[i][k+])*tmp;
             }
             printf("%.6f%c",ans,i==n?'\n':' ');
         }
     }
     return ;
 }