Fantasia (点强连通分量建图 + 树形DP)

简化一下题意，我们先看成一副强连通的图，这时候应该是最简单了，去点任意点都是其他的乘积。那再加强一点难度，改为两个强连通图连接的非强连通图呢？那应该就是找出关键的那个点，并求出两边的乘积。但是一个一个去找是不可能的。

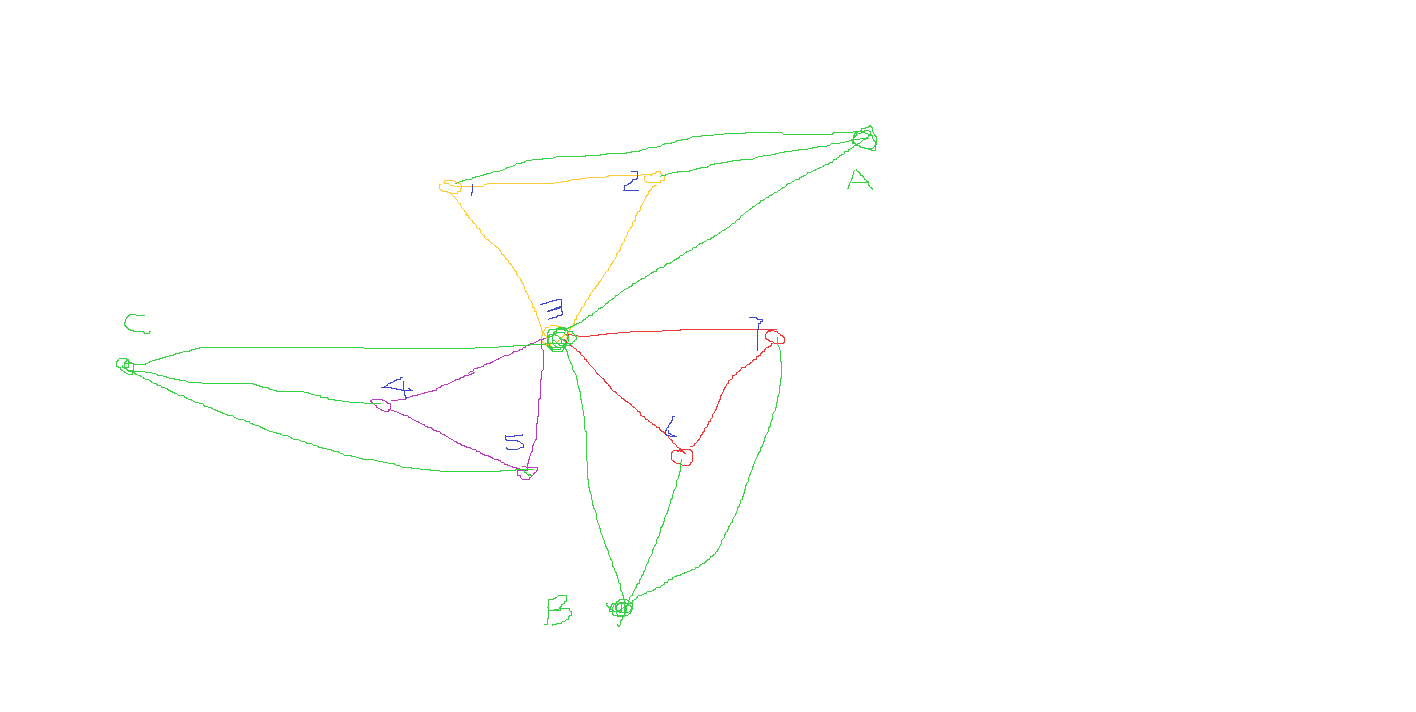
假设如图中的非绿色线是题目给的图。然后我们根据强连通分量去新建一副如图中绿色线条的图，那么这时候我们就把原图转化为以可树了。。对于每一个点我们求的是该点以及以下的乘积。然后我们从A出发这时候我们发现A点的值刚好就是整幅图的乘积。这时候如果我们需要求删除3这个点的得到的结果应该就是整一副图去除以3点及一下的乘积得到1，2的乘积，再加上3点的子树的乘积和也就是4、5 和 6、7的乘积和。

这道题目的难点就是转化建图的那一个步骤，应该说是最核心的部分。

#include<bits/stdc++.h>
#define LL long long
using namespace std;

const int maxn = 1e5 + ;
const LL  mod  = 1e9 + ;

LL n, w[maxn], vis[maxn << 1], sum[maxn << 1], pro[maxn << 1];

struct oldEdge{
    int v, next;
    bool flag;
};
int oldHead[maxn], ocnt;
oldEdge oedge[maxn << ];

void addOldEdge(int u, int v){
    oedge[ocnt].v = v;
    oedge[ocnt].flag = false;
    oedge[ocnt].next = oldHead[u];
    oldHead[u] = ocnt ++;
}

struct newEdge{
    int v, next;
};
int newHead[maxn << ], ncnt;
newEdge nedge[maxn << ];

void addNewEdge(int u, int v){
    nedge[ncnt].v = v;
    nedge[ncnt].next = newHead[u];
    newHead[u] = ncnt ++;
}

int dfn[maxn], low[maxn], root[maxn], rn, cnt;
stack<int>sta;

void tarjan(int u, int fa){
    dfn[u] = low[u] = ++cnt;
    for(int i = oldHead[u]; i != -; i = oedge[i].next){
        if(oedge[i].flag) continue;
        oedge[i].flag = oedge[i ^ ].flag = true;
        sta.push(i);
        int v = oedge[i].v;

        if(dfn[v]){
            low[u] = min(low[u], dfn[v]);
            continue;
        }
        tarjan(v, fa);
        low[u] = min(low[u], low[v]);

        if(low[v] >= dfn[u]){
            rn ++;
            int ek;
            do{
                ek = sta.top();sta.pop();
                root[oedge[ek].v] = root[oedge[ek ^ ].v] = fa;
                addNewEdge(rn, oedge[ek].v); addNewEdge(oedge[ek].v, rn);
                addNewEdge(rn, oedge[ek ^ ].v); addNewEdge(oedge[ek ^ ].v, rn);
            }while(oedge[ek ^ ].v != u);
        }
    }
}

void dfs(int u){
    vis[u] = true;
    sum[u] = ;
    pro[u] = (u <= n) ? w[u] : ;
    for(int i = newHead[u]; i != -; i = nedge[i].next){
        int v = nedge[i].v;
        if(vis[v]) continue;
        dfs(v);
        if(u <= n)
            sum[u] = (sum[u] + pro[v]) % mod;
        pro[u] = pro[u] * pro[v] % mod;
    }
}

LL inv(LL a){
    int p = mod - ;
    LL ret = ;
    while(p){
        if(p & )ret = ret * a % mod;
        a = a * a % mod;
        p >>= ;
    }
    return ret;
}

void init(){
    memset(root, , sizeof(root));
    memset(newHead, -, sizeof(newHead));
    memset(oldHead, -, sizeof(oldHead));
    memset(dfn, , sizeof(dfn));
    memset(vis, false, sizeof(vis));
    ncnt = ocnt = cnt = ;
}

int main(){
    int T, m, a, b;scanf("%d",&T);
    while(T --){
        scanf("%lld%d",&n,&m);
        init();rn = n;
        for(int i = ; i <= n; i ++)scanf("%lld",&w[i]);
        for(int i = ; i < m; i ++){
            scanf("%d%d",&a,&b);
            addOldEdge(a,b);
            addOldEdge(b,a);
        }
        for(int i = ; i <= n; i ++)
            if(!dfn[i])tarjan(i, rn + );

        LL tot = ;
        for(int i = ; i <= n; i ++){
            if(vis[i]) continue;
            if(root[i]){
                dfs(root[i]);
                tot = (tot + pro[root[i]]) %mod;
            }else
                tot = (tot + w[i]) % mod;
        }
        LL ans = ;
        for(int i = ; i <= n; i ++){
            if(root[i]){
                LL temp = ((tot - pro[root[i]] + pro[root[i]] * inv(pro[i]) + sum[i]) % mod + mod) * i % mod;
                ans = (ans + temp) % mod;
            }
            else
                ans = ((ans + (tot - w[i]) * i) % mod + mod) % mod;
        }
        printf("%lld\n",ans);
    }
    return ;
}