从池子里的beta看秋香, 个性迥异
从池子里的beta看秋香, 个性迥异
前文里那十只个股为例, 统计了它们的beta值.
回顾如下:
Num name code Beta
0 深圳燃气 601139 0.710 公用事业
1 分众传媒 002027 1.258 中小板
2 海康威视 002415 1.288 中小板
3 双汇发展 000895 0.772 食品
4 柳 工 000528 1.336 工程机械
5 上海银行 601229 0.580 银行
6 华兰生物 002007 0.861 医药
7 兖州煤业 600188 1.286 煤炭
8 云铝股份 000807 1.615 有色金属
9 神火股份 000933 1.650 有色金属
有色金属: 1.6 最骚
煤炭/机械 1.3 次骚
中小板龙头 1.2 大众情人
食品医药 0.8 相对平稳
公用事业 0.7 平稳
银行 0.6 波动最小, 最温柔
想看看不同时期的身段, 好勒!
代码
def load_symbols(subset=(8,18,1), start='2017-01-01', ):
'''
>>> symbols=('000933.sz','000069.sz','002027.sz')
>>> stks = load_symbols()
>>> pl.plot_muti_ohlc(stks,subs='2017',)
>>> pl.plot_muti_ohlc(stks,subs=slice(-350, None))
>>> pl.plot_muti_ohlc(stks,subs=slice(-500, None))
>>> pl.plot_muti_ohlc(stks,subs=slice(100,200,1))
'''
syms_, symbols = read_zxg(subset)
stks=[]
for i,s in enumerate(symbols):
stk=load_symbol(s, )
stks.append(stk)
return stks
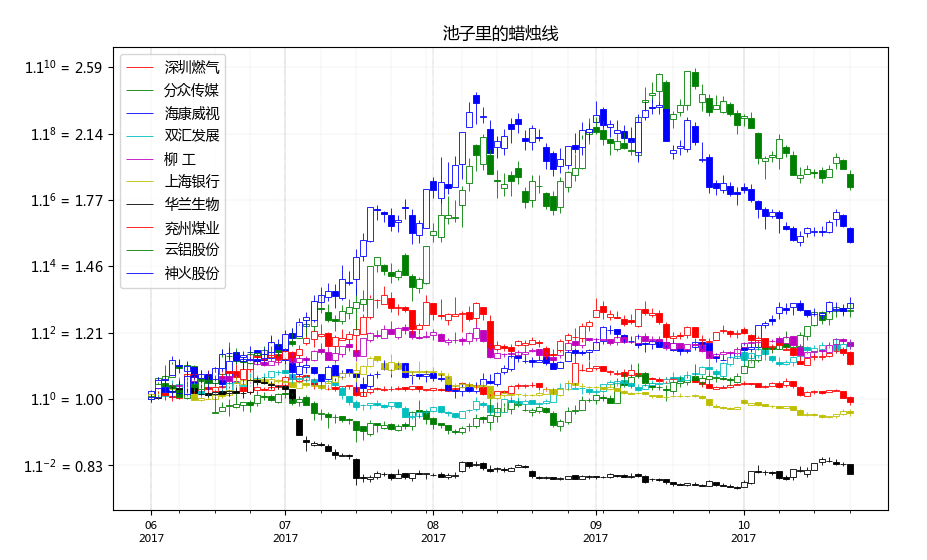
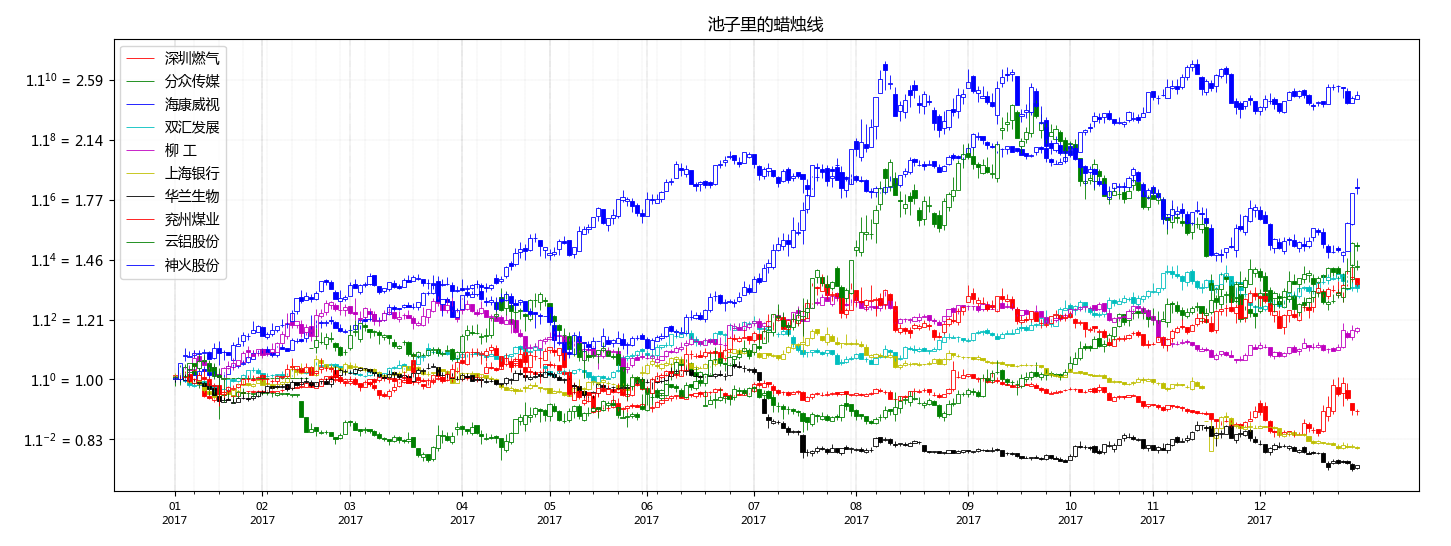
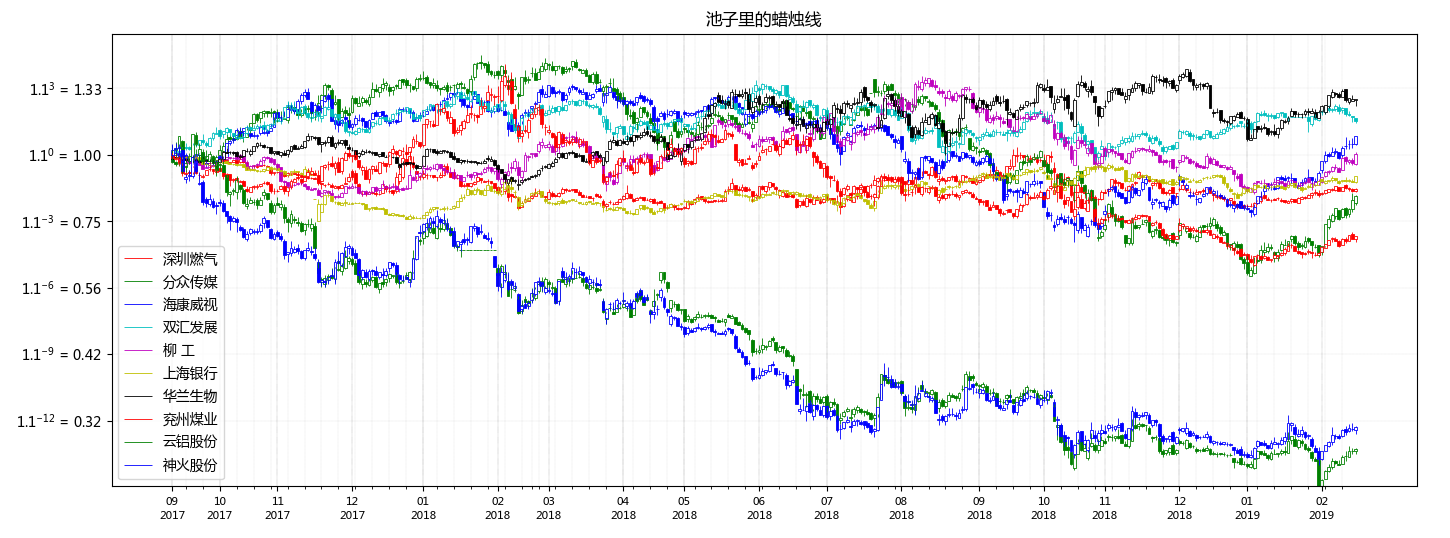
结果图:
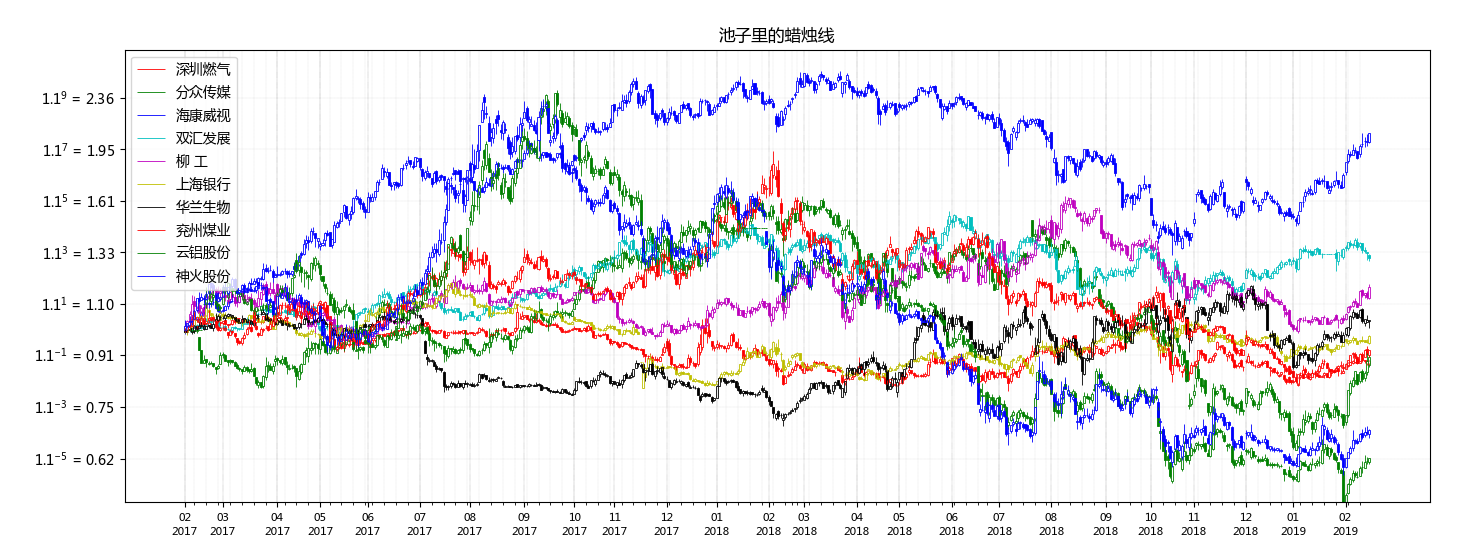
从池子里的beta看秋香, 个性迥异的更多相关文章
- 学习sql中的排列组合,在园子里搜着看于是。。。
学习sql中的排列组合,在园子里搜着看,看到篇文章,于是自己(新手)用了最最原始的sql去写出来: --需求----B, C, F, M and S住在一座房子的不同楼层.--B 不住顶层.C 不住底 ...
- 我存在,你深深的循环里--从反射看JSON死循环
JSON有一个非常经典的问题:JSONException: There is a cycle in the hierarchy!俗称死循环.解决这个问题至少有三种以上的办法,总之一句话就是过滤.今 ...
- 带着新人看java虚拟机04(多线程篇)
我记得最开始接触多进程,多线程这一块的时候我不是怎么理解,为什么要有多线程啊?多线程到底是个什么鬼啊?我一个程序好好的就可以运行为什么要用到多线程啊?反正我是十分费解,即使过了很长时间我还是不是很懂, ...
- 个股和股票池的beta系数的估算
个股的beta系数的估算 代码 def test_gg_beta(symbol='000895.sz', start='2018-01-01', plot_price=True, align_to=' ...
- 你真的懂ThreadPoolExecutor线程池技术吗?看了源码你会有全新的认识
Java是一门多线程的语言,基本上生产环境的Java项目都离不开多线程.而线程则是其中最重要的系统资源之一,如果这个资源利用得不好,很容易导致程序低效率,甚至是出问题. 有以下场景,有个电话拨打系统, ...
- 关于Java 里的String和对象
之前老师在课堂上讲过关于Java的引用,但是很遗憾,木有认真听啊,所以就在学习Java的过程中迷惑迷惑...最近好像明白一点Java的引用是怎么回事了.以下仅是我个人的理解,如果不对,还请不吝赐教. ...
- 相机拍的图,电脑上画的图,word里的文字,电脑屏幕,手机屏幕,相机屏幕显示大小一切的一切都搞明白了!
相机拍的图,电脑上画的图,word里的文字,电脑屏幕,手机屏幕,相机屏幕显示大小一切的一切都搞明白了! 先说图片X×dpi=点数dotX是图片实际尺寸,简单点,我们只算图片的高吧,比如说拍了张图片14 ...
- 常看常遇见之一——BS架构VS CS架构
常看常遇见之一——BS架构VS CS架构 1.BS架构 即Browser/Server(浏览器/服务器)结构,是随着Internet技术的兴起,对C/S结构的一种变化或者改进的结构.在这种结构下,用户 ...
- Practical Malware Analysis里有关inetsim\APATEDNS
以前从未接触过linux,碰到了许多问题,按步骤: 1\安装VMWARE,安装ubuntu16.04 问题1:之前装的是VM10,装完后没有安装VMTOOLS,我点安装 VMTOOLS,它弹出“简易安 ...
随机推荐
- Linux CentOS7 安装php简要过程以及nginx
Copy From https://www.cnblogs.com/freeweb/p/5425554.html 修改了下: 1. 下载php源码: wget http://cn2.php.net ...
- Windows 安装补丁的另外一种方法
Windows的补丁安装时经常出现异常提示: 如果安装不上的话 可以使用dism的方式来进行安装: 具体方法: 1. 将补丁包 一般为msu 或者是exe文件,改成rar后缀,并且解压缩,获取cab文 ...
- [转帖]Tensor是神马?为什么还会Flow?
Tensor是神马?为什么还会Flow? 互联网爱好者 百家号17-05-2310:03 大数据文摘作品,转载要求见文末 编译 | 邵胖胖,江凡,笪洁琼,Aileen 也许你已经下载了TensorFl ...
- [日常工作]GS使用安装盘修改密码后的处理
1. GS服务器端有时候需要修改 9999 的用户密码.但是修改完密码之后有几个注意事项: 一般有两个可以修改注册的地方: 使用setup里面的修改用户密码 修改完密码之后要手工注册一下数据库实例 也 ...
- PostgreSQL、SQL Server数据库中的数据类型的映射关系
PostgreSQL 8.1 轰动发布,我也打算将原来使用 SQL Server 的一些应用迁移到 PostgreSQL 上,首先需要迁移的是表,那么这就必须要先搞清楚这两个数据库中的数据类型的映射关 ...
- jquery html 獲取或設置
jquery提供操作html元素的屬性和內容的強大方法. DOM就是獨立于平台和語言的界面,允許程序和腳本動態訪問和改變DOM的內容,結構和樣式. 獲取內容:text(),html(),val(),a ...
- python之导入模块
导入模块的方法: 导入整个模块:import module_name 导入特定函数:from module_name import function_name 给函数指定别名:from module_ ...
- yield与递归的组合运用
- LightOJ - 1074 Extended Traffic(标记负环)
题意:有n个城市,每一个城市有一个拥挤度ai,从一个城市u到另一个城市v的时间为:(au-av)^3,存在负环.问从第一个城市到达第k个城市所话的时间,如果不能到达,或者时间小于3输出?否则输出所花的 ...
- hg和git命令对照表
hg和git命令对照表 来源 https://github.com/sympy/sympy/wiki/Git-hg-rosetta-stone Git hg rosetta stone muxat ...
