【逆向工具】IDA使用2-VS2015版本release查找main函数入口，局部变量

VS2015版本release查找main函数入口

vc++开发的程序main或WinMain函数是语法规定的用户入口，而不是应用程序入口。入口代码是mainCRTstartup、wmainCRTStartup、WinMainCRTSartup或wWinMainCRTStarup，具体情况由编译器制定。

VS2015版本debug查找main函数在《VS程序反汇编找main函数》。release版本找main函数入口有所区别的地方在于一开始就单步步过一个call指令，jmp跳转。然后经过三个push，进入call内到达用户入口，而且需要注意用户入口点是程序员自己也是可以修改的。

VC编译器的版本不同，mainCRTSartup函数也可能会有所不同，IDA中将mainCRTSartup函数命名为___tmainCRTStartup。

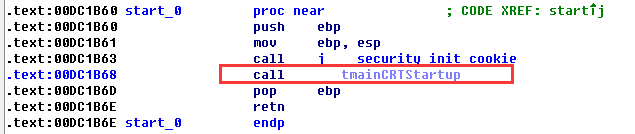
main函数有三个参数，分别为命令行参数个数、命令行参数信息和环境变量信息。根据main函数调用的特征会将3个参数压入栈内作为函数的参数。所以查找用户入口main()前必然会有3个push指令。

IDA中的基本数据类型-局部变量

测试代码

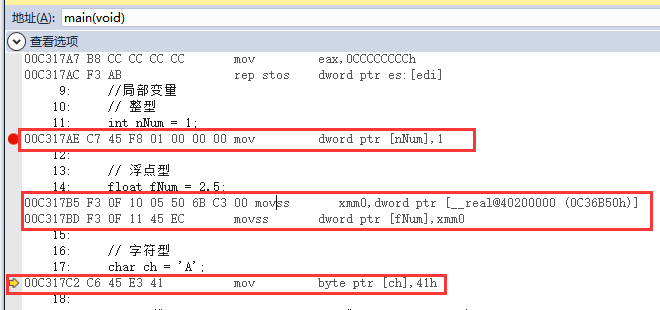
局部变量有三个int、float、char。分别赋值。

int main()
{
	//局部变量
	// 整型
	int nNum = 1;

	// 浮点型
	float fNum = 2.5;

	// 字符型
	char ch = 'A';

	printf("int %d , float %f ,char %c", nNum, fNum, ch);

    return 0;
}

vs反汇编结果

在掌握IDA反汇编工具之前，先调试VS编译的debug版本程序熟悉int 型变量、float型变量、char型变量反汇编后的指令，因为经过VS编译器优化过所以看起来比较容易理解。VS快捷键【alt+8】打开反汇编窗口。

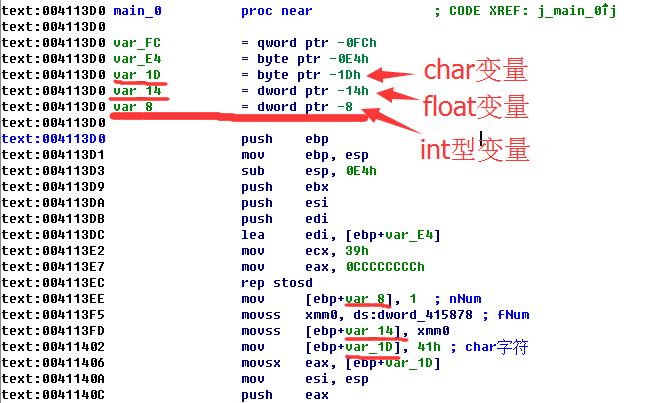
IDA汇编结果

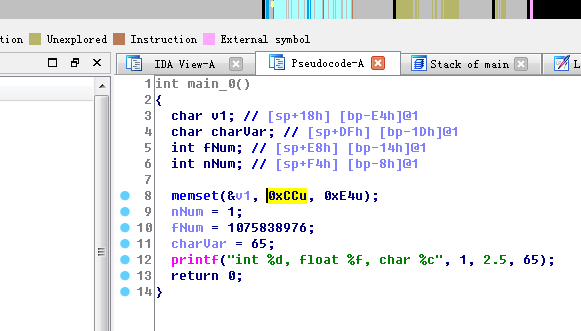
IDA的逆向结果中 var_ 是局部变量，为了让逆向时更容易弄懂这些参数。可以使用快捷键【n】将变量改名。

在IDAF5键大法转换为源码前，可以看到float型变量是16进制，char变量是16进制。那么我们可以点击数值，右键或者R键将char型变量的值直接显示出来。

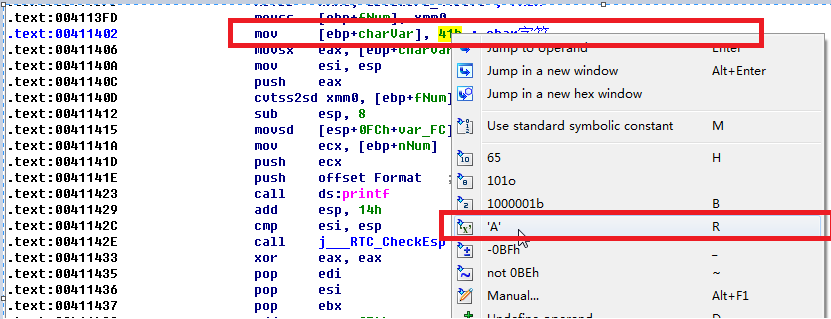
而float型变量双击dword_415878，在IDA中【edit】->【Operand type】->【Number】->【Floatingpoint】，将值改为float显示。这里将40200000h转换成了2.5。

.text:004113F5                 movss   xmm0, ds:dword_415878 ; fNum

修改之后的反汇编代码。

再次按F5后，IDA将反汇编的源码转换后我们可以得到与源码近乎相同的伪C代码，但是变量类型上还有一些偏差。

参考：

C++反汇编与逆向分析技术揭秘，46页