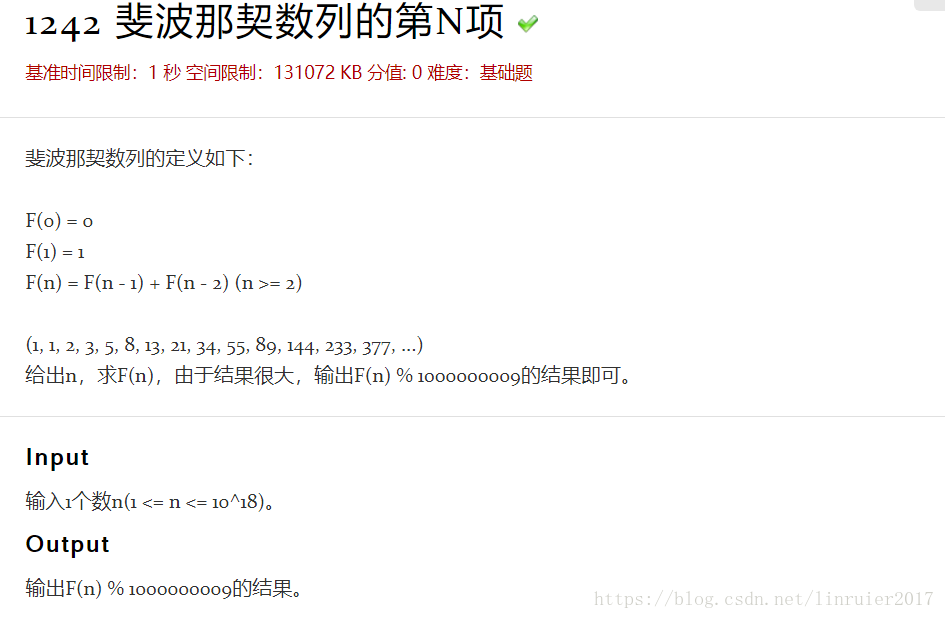
51 Nod 1242 矩阵快速幂求斐波那契数列

#include<bits/stdc++.h>
#define mod 1000000009
using namespace std;
typedef long long ll;
typedef long long LL;
struct Mat
{
    LL mat[3][3];
    Mat()
    {
        memset(mat,0,sizeof(mat));
    }
    LL* operator [](int x)    //注意这种写法
    {
        return mat[x];
    }
} A;
Mat Mut(Mat a,Mat b)
{
    Mat c;
    for(int k=0; k<3; k++)
        for(int i=0; i<3; i++)
            for(int j=0; j<3; j++)
            {
                c[i][j]+=a[i][k]*b[k][j]%mod;
                c[i][j]=c[i][j]%mod;
            }
    return c;
}
Mat Qpow(Mat a,LL n)
{
    Mat c;
    for(int i=0; i<3; ++i)
        c[i][i]=1;
    for(; n; n>>=1)
    {
        if(n&1) c=Mut(c,a);
        a=Mut(a,a);
    }
    return c;
}

ll hh[3][3]={{1,1,0},{0,1,1},{0,1,0}};
int main()
{
    for(int i=0;i<3;i++)
        for(int j=0;j<3;j++)
        A.mat[i][j]=hh[i][j];

    ll n;
    cin>>n;
    if(n==0){cout<<0<<endl;return 0;}
    if(n==1){cout<<1<<endl;return 0;}
    if(n==2){cout<<1<<endl;return 0;}
    if(n==3){cout<<2<<endl;return 0;}
    A=Qpow(A,n-3);
    ll ans=((A.mat[0][0]*2%mod+A.mat[0][1])%mod+A.mat[0][2])%mod;
    cout<<ans<<endl;
    return 0;
}