P2532 [AHOI2012]树屋阶梯

题目：P2532 [AHOI2012]树屋阶梯

思路：

打表之后不难看出是裸的Catalan数。简单证明一下：

对于任意一种合法方案，都可以表示为在左下角先放一个\(k*(n+1-k),k\in[1,n]\)的矩形，再在矩形的上边和右边分别放\(k-1\)阶台阶和\(n-k\)阶台阶。

例如下图（从luogu题解中盗的图...）：

在左下角先放了一个\(2*3\)的矩形，之后在矩形上边放\(1\)阶台阶，在矩形右边放\(2\)阶台阶。



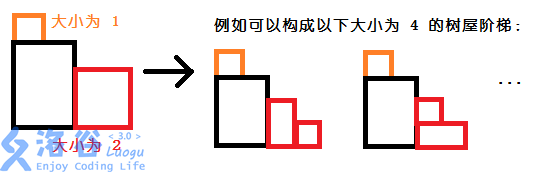
不难看出矩形上边和右边两部分独立，只要枚举左下矩阵长度，对每种矩形，把上边和右边的方案数相乘（乘法原理），再把不同矩形长度得到的答案相加（加法原理）就能得到总方案数。

设\(h(n)\)为n阶台阶方案数，得到递推式\(h(n)=\sum_{k=1}^nh(k-1)*h(n-k)\),就是Catalan数。

计算时分解质因数即可。

---

Code：

#include <bits/stdc++.h>
using namespace std;
const int N = 5000,base=10000,power=4;
int n,tot,p[N],mindiv[N],cnt[N];
struct bigint{
	int len,d[N];
	inline bigint (){
		memset(d,0,sizeof(d));
		len=1;
	}
	inline bigint(int num){
		len=1;
		d[1]=num;
	}
	void clean(){
		while(len>1&&!d[len]) --len;
	}
	inline bigint operator * (const bigint &b)const{
		bigint c;
		c.len=len+b.len;
		for(int i=1;i<=len;++i) for(int j=1;j<=b.len;++j)
			c.d[i+j-1]+=d[i]*b.d[j],c.d[i+j]+=c.d[i+j-1]/base,c.d[i+j-1]%=base;
		c.clean();
		return c;
	}
	inline void print(){
		clean();
		printf("%d",d[len]);
		for(int i=len-1;i;--i) printf("%0*d",power,d[i]);
	}
};
void Prime(){
	for(int i=2;i<=2*n;++i){
		if(!mindiv[i]) mindiv[i]=p[++tot]=i;
		for(int j=1;j<=tot;++j){
			if(i*p[j]>2*n||p[j]>mindiv[i]) break;
			mindiv[i*p[j]]=p[j];
		}
	}
}
void add(int num){
	while(num^1){
		++cnt[mindiv[num]];
		num/=mindiv[num];
	}
}
void del(int num){
	while(num^1){
		--cnt[mindiv[num]];
		num/=mindiv[num];
	}
}
bigint quickpow(int a,int b){
	bigint res=1,c=a;
	while(b){
		if(b&1) res=res*c;
		c=c*c;
		b>>=1;
	}
	return res;
}
bigint Catalan(int n){
	for(int i=n+2;i<=2*n;++i) add(i);
	for(int i=1;i<=n;++i) del(i);
	bigint res=1;
	for(int i=1;i<=tot;++i) res=res*quickpow(p[i],cnt[p[i]]);
	return res;
}
int main(){
	scanf("%d",&n);
	Prime();
	Catalan(n).print();
	return 0;
}