csp 初赛 （不懂的地方）

11. 有以下结构体说明和变量定义，如图所示，指针 p、 q、 r 分别指向一个链表中的三个连续结点。

struct node {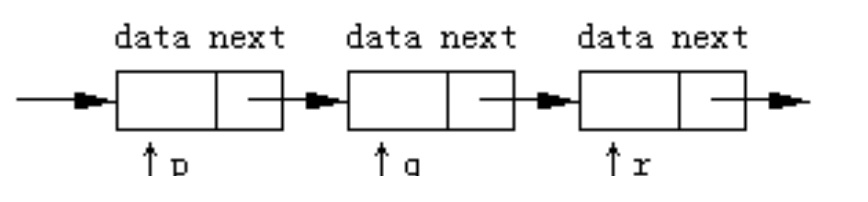                        
int data;
struct node *next;
} *p, *q, *r;
现要将 q 和 r 所指结点的先后位置交换，同时要保持链表的连续，以下程序段中错误
的是（ D ）

A. q->next = r->next; p->next = r; r->next = q;
B. p->next = r; q->next = r->next; r->next = q;
C. q->next = r->next; r->next = q; p->next = r;
D. r->next = q; q->next = r->next; p->next = r;

->是什么意思啊，指针没有学啊qaq  ///

q>nest 就是 bian[q].net 的值

完全图？？？

在无向图中，若每对顶点之间都有一条边相连，则称该图为完全图
在有向图中，若每对顶点之间都有二条有向边相互连接，则称该图为完全图

逻辑运算。

转载：https://blog.csdn.net/mengzhengjie/article/details/80611422

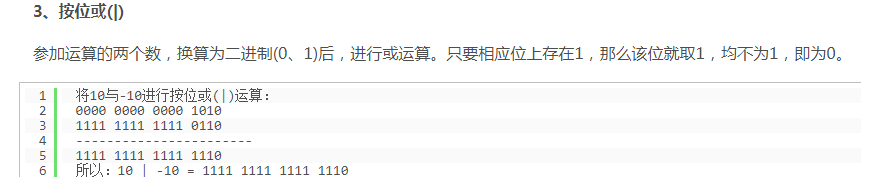
任何数与0^都是他本身

二叉树不能表示图

组合数学

大佬博客：https://blog.csdn.net/anglanjing7414/article/details/101189740

5.常用组合数公式

(1)C(n,m)=C(n-1,m)+C(n-1,m-1)
(2)C(n,m)=C(n,n-m)
(3)C(n,m+1)=(n-m)/(m+1)*C(n,m)

疑惑

单选题（1）某计算机的 CPU 和内存之间的地址总线宽度是 32 位（bit），这台计算机最多可以使用（　　）的内存。

A. 2GB　　B. 4GB　　C. 8GB　　D. 16GB

32位bit就是 2^32 Byte

如何把该式子转换成后缀或前缀表达式呢？其实就是分三步：

《哈夫曼树 》二叉树

？比大小 语法。 语句 1？语句2：语句3 （当语句1满足 就语句2,不然语句3）

时间复杂度，程序语言，数学：组合，概率；printf("")

printf(",%04d",D[i]);

%04d 表示在输出一个小于4位的数值时, 将在前面补0使其总宽度为4位