Backbone.js 1.0.0源码架构分析(一)

Backbone.js 是javascript 语言中 首个实现MVC设计模式的类库，API接口方法重度依赖于underscore.js，DOM选择器则依赖于jQuery.js或者zepto.js。

Backbone.js 1.0.0 现在既可以支持浏览器端js代码，也可以支持服务端nodejs环境代码。为了实现这个兼容性，Backbone.js 采用了在函数表达式中传进‘this’关键词来映射宿主环境的全局变量（在browser为 ‘window’对象，在nodejs环境为'exports'）:

(function(){

  // 初始设定
  // -------------

  // 保存全局对象在本地的引用
  var root = this;

  // 如果我们在引入backbone.js之前，全局对象已经存在Backbone属性，则先把它引入到本地变量，以便Backbone.noConfllict()的实现解决命名空间冲突
  var previousBackbone = root.Backbone;

  //创建数组方法在本地的引用，以便于后面利用
  var array = [];
  var push = array.push;
  var slice = array.slice;
  var splice = array.splice;

  // 顶级命名空间的声明，后面模块与方法都将追加到此命名空间之下
  if (typeof exports !== 'undefined') {
    //nodejs环境中声明
    Backbone = exports;
  } else {
    //browser中声明，并且添加到全局对象中
    Backbone = root.Backbone = {};
  }

  // 版本声明
  Backbone.VERSION = '1.0.0';

  // browser端，保存backbone.js所依赖的 underscore.js 声明的 全局变量
  var _ = root._;
  // nodejs中，通过require方式引入underscore.js
  if (!_ && (typeof require !== 'undefined')) _ = require('underscore');

  // 保存Jquery或Zepto等DOM选择器、操作类库所声明的全局变量在本地的引用
  Backbone.$ = root.jQuery || root.Zepto || root.ender || root.$;

  // 进入非冲突模式，即Backbone的变量已经存在，我们就退而避之，将backbone.js换做其他变量名
  Backbone.noConflict = function() {
    root.Backbone = previousBackbone;
    return this;
  };
  // backbone各APT方法的实现
}).call(this);

　　一个js框架或者类库在编写的时候，首先要为自己‘正名’，如此，才能够扬名立万。

既然名已正，其内功招式就可以正常地表现了。

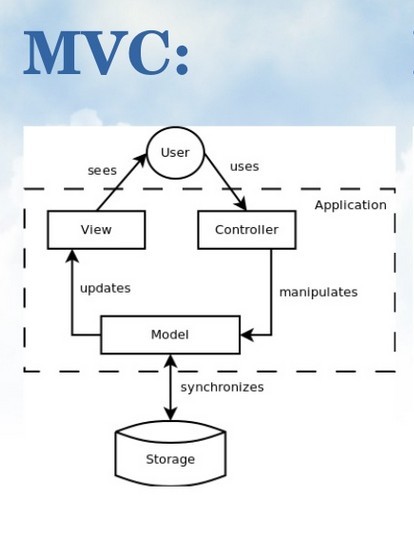
Backbone 既然有 MVC 之名，那我们就来先看看MVC的典型架构吧：

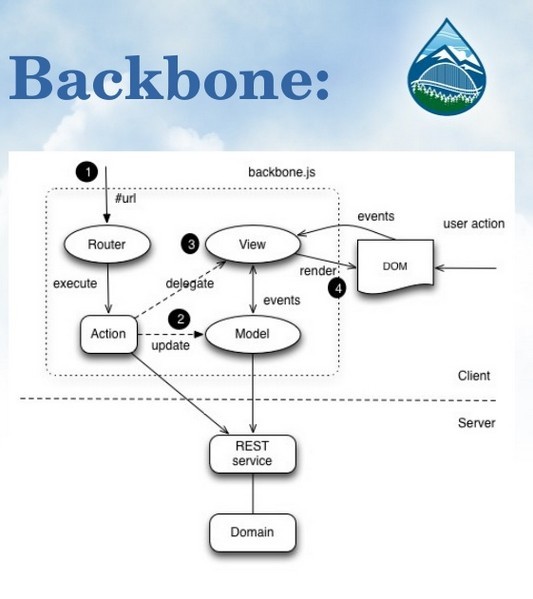
而backbone.js 可以这样实现

1、自定义model与collection

2、定义渲染model的视图view

3、定义渲染collection的视图view

4、引入视图渲染模板