最长公共子序列（LCS）和最长递增子序列（LIS）的求解

一、最长公共子序列

　　经典的动态规划问题，大概的陈述如下：

　　给定两个序列a1,a2,a3,a4,a5,a6......和b1,b2,b3,b4,b5,b6.......,要求这样的序列使得c同时是这两个序列中的部分（不要求连续），这个就叫做公共子序列，然后最长公共子序列自然就是所有的子序列中最长的啦。

　　既然是动态规划，难点肯定是在转移方程那了。首先我们用一张网上流传的图：

　　我个人觉得这张图最好的阐述了这个问题的解法。下面说一下我的理解：首先我们要考虑怎么表示LCS中的各个状态，这个知道的可能觉得很简单，但是不知道的可能想很久也想不到，我就是在看到这张图才真正理解为什么要采用二维数组表示这个状态（可能不同的人理解不同）。我们用f[i][j]表示字符串a的前i个与字符串b的前j个的最长公共子串，则状态转移方程是：

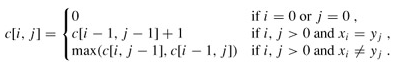
现在我们通过上面的那个图来理解一下这个方程，这个图显示的是求ABCBDAB与BDCABA的LCS，首先当某一个串为零，公共子串自然也为0了，然后如果某一个值上两个串相同那么自然是加一，最后不等的时候由图可以看到他们的来源有两个防线即上方和左方，通过这个我们就可以一步一步求出最大的公共子串了。

 /*
 总结：这个是经典的LCS问题，主要是要找到递归方程
 状态用二维数组表示（想到这个是难点）用f[a][b],表示字符串
 A中前a个与字符串B中前b个的最大公共子串
 递归方程：
 f[i][j]=  f[i-1][j-1]+1(相等的时候)
           max(f[i][j-1],f[i-1][j])(不等的时候)
 */
 #include<iostream>
 #include<algorithm>
 #include<cstdio>
 #include<queue>
 #include<cstring>
 #include<cmath>
 using namespace std;
 int main()
 {
     string a,b;
     while(cin>>a>>b){
         int dp[][]={};
         int la=a.length();
         int lb=b.length();
         int maxx=;
         for(int i=;i<la;i++){
             for(int j=;j<lb;j++){
                 if(a[i]==b[j]){
                     dp[i+][j+]=dp[i][j]+;
                     if(maxx<dp[i+][j+])
                     maxx=dp[i+][j+];
                 }
                 else{
                     dp[i+][j+]=max(dp[i][j+],dp[i+][j]);
                 }
             }
         }
         cout<<maxx<<endl;
     }
     return ;
 }

　　最后再稍微说一点最长公共子序列的用途，这个算法的一种用途就是用来判断两段文字的相似度，举一个我们最熟悉的例子，有两段程序，一段是原版，一段使用改变量名等手段做出来的那么他们的最长公共子序列一定会比较长，也就是说这个可以帮助我们找到看起来很不同的东西中的许多共同点。

二、最长递增子序列

　　子序列这里就不用再介绍了，最长递增子序列也很好理解，就是给定一个序列 A_n = a₁ ,a₂ ,  ... , a_n ，找出最长的子序列使得对所有 i < j ，a_i < a_j 。。这个问题又是一个动态规划。它有两种解决方案：

　　1、转化成LCS问题求解，初看这个貌似是没什么关系，但是我们至腰间这个序列排序之后与原来的求LCS得到的就是LIS了，个人觉得这个特别的　　　　好，如果你自己能想出来那么你对LCS的理解也有一定深度了。

　　2、继续动态规划，首先我们用f[i]表示以i结尾的ＬＩＳ的长度，，这时我们就要考虑ｆ［ｉ］与前面那些值的关系，即这个值是要加载他前面那　　　　个比他小的值上，这样才能达到最长。初始值自然是全部为１。

这里就不直接贴代码了，太简单了，给一个有一定改动的例子（其实没有本质性变化），合唱团:

题目描述：

N位同学站成一排，音乐老师要请其中的(N-K)位同学出列，使得剩下的K位同学不交换位置就能排成合唱队形。
合唱队形是指这样的一种队形：设K位同学从左到右依次编号为1, 2, …, K，他们的身高分别为T1, T2, …, TK，
则他们的身高满足T1 < T2 < … < Ti , Ti > Ti+1 > … > TK (1 <= i <= K)。
你的任务是，已知所有N位同学的身高，计算最少需要几位同学出列，可以使得剩下的同学排成合唱队形。

输入：

输入的第一行是一个整数N（2 <= N <= 100），表示同学的总数。
第一行有n个整数，用空格分隔，第i个整数Ti（130 <= Ti <= 230）是第i位同学的身高（厘米）。

输出：

可能包括多组测试数据，对于每组数据，
输出包括一行，这一行只包含一个整数，就是最少需要几位同学出列。

 /*
 总结：这个是经典的LIS问题两种解决方法：
 一、排序后转换成LCS
 二、直接找转化方程，令L[i]表示以i结尾的最长递增子串长度，
 则L[i]=max(l[j]+1,1)其中j表示前面小于i的且a[i]>a[j]的值
 */
 #include<iostream>
 #include<algorithm>
 #include<cstdio>
 #include<queue>
 #include<cstring>
 #include<cmath>
 using namespace std;
 int main()
 {
     int n;
     while(scanf("%d",&n)==&&n){
         int a[];
         int b[];
         int c[];
         int d[];
         for(int i=;i<n;i++){
             b[i]=;
             c[i]=;
             d[i]=;
             scanf("%d",&a[i]);
             for(int j=i-;j>=;j--){
                 if(a[i]>a[j]){
                     b[i]=max(b[i],b[j]+);
                 }
             }
         }
         for(int i=n-;i>=;i--){
             for(int j=i+;j<n;j++){
                 if(a[i]>a[j]){
                     c[i]=max(c[i],c[j]+);
                 }
             }
         }
         int maxx=;
         for(int i=;i<n;i++){
             d[i]=b[i]+c[i];
             //cout<<b[i]<<ends<<c[i]<<ends<<d[i]<<endl;
         }
         for(int i=;i<n;i++){
             if(maxx<d[i]){
                 maxx=d[i];
             }
         }
         printf("%d\n",n-maxx+);
     }
     return ;
 }