视觉SLAM第四讲李群与李代数习题
视觉SLAM第四讲李群与李代数习题
一、验证\(SO(3)、SE(3)、SIM(3)\)关于乘法成群
首先引入一下群的定义。
群 (Group) 是一种集合加上一种运算的代数结构。我们把集合记作 \(A\), 运算记作 \(.\),那么一个群可以记作 \(G=(A, \cdot)\) 。群要求这个运算满足以下几个条件:
封闭性: \(\forall a_1, a_2 \in A, \quad a_1 \cdot a_2 \in A\).
结合律: \(\forall a_1, a_2, a_3 \in A, \quad\left(a_1 \cdot a_2\right) \cdot a_3=a_1 \cdot\left(a_2 \cdot a_3\right)\).
么元: \(\exists a_0 \in A\), s.t. \(\forall a \in A, \quad a_0 \cdot a=a \cdot a_0=a\).
逆: \(\forall a \in A,\quad \exists a^{-1} \in A, \quad\) s.t. \(a \cdot a^{-1}=a_0\).
- 首先验证 \(SO(3)\)关于乘法成群
\]
封闭性:
设任意\(R_1,R_2 \in SO(3)\),则有:
\]
此时,\(R_1,R_2\)的乘法结果属于正交矩阵得证;
\]
此时,\(R_1,R_2\)的乘法结果行列式值为1得证;
综上,对于任意\(R_1,R_2 \in SO(3)\),有\(R_1R_2 \in SO(3)\)。
结合律:
由于矩阵乘法是满足结合律的,所以有:
\]
么元:
对于单位矩阵\(I \in SO(3)\),容易证明其是么元。
任意\(R \in SO(3)\)
\]
逆:
根据\(SO(3)\)的定义,容易验证,对于任意的\(R \in SO(3),\exist (R^T = R^{-1})\in SO(3)\),使得\(RR_{-1} = I\)。
- 验证 \(SE(3)\)关于乘法成群
\[SE(3) = \{\mathbf{T} =
\begin{bmatrix}
\mathbf{R} & \mathbf{t}\\
\mathbf{0} & 1
\end{bmatrix}
\in \mathbb{R}^{4\times 4} | \mathbf{R} \in SO(3), \mathbf{t}\in \mathbb{R}^3
\}
\]
封闭性:
设任意\(\mathbf{T_1} =
\begin{bmatrix}
\mathbf{R_1} & \mathbf{t_1}\\
\mathbf{0} & 1
\end{bmatrix},\mathbf{T_2} =
\begin{bmatrix}
\mathbf{R_2} & \mathbf{t_2}\\
\mathbf{0} & 1
\end{bmatrix}\),则有:
\begin{bmatrix}
\mathbf{R_1R_2} & \mathbf{R_1t_2+t_1}\\
\mathbf{0} & 1
\end{bmatrix}
\]
由上一题的证明,有\(R1R_2 \in SO(3)\),根据矩阵维数得到$R_1t_2+t_1 \in\mathbb{R}^3 $
所以,\(T_1T_2 \in SE(3)\)
结合律:
由于矩阵乘法是满足结合律的,所以有:
\]
么元:
对于单位矩阵\(I \in SE(3)\),容易证明其是么元。
任意\(T \in SE(3)\)
\]
逆:
根据\(SE(3)\)的定义,对于任意\(\mathbf{T} =
\begin{bmatrix}
\mathbf{R} & \mathbf{t}\\
\mathbf{0} & 1
\end{bmatrix} \in SE(3)\),我们设\(T' = \begin{bmatrix}
\mathbf{R^{-1}} & \mathbf{-R^{-1}t}\\
\mathbf{0} & 1
\end{bmatrix} \in SE(3)\),
容易验证$TT' = I $
验证\(SIM(3)\)关于乘法成群
\(SIM(3)\),就是在\(T\)的基础上添加了一个尺度变化因子\(s\)。
\begin{bmatrix}
\mathbf{sR} & \mathbf{t}\\
\mathbf{0} & 1
\end{bmatrix}
\in \mathbb{R}^{4\times 4} | \mathbf{R} \in SO(3), \mathbf{t}\in \mathbb{R}^3,s \in \mathbb{R}
\}
\]
其证明\(SE(3)\)类似,不再赘述。
二、验证\((\mathbb{R}^3,R,\times)\)构成李代数
首先引入一下李代数的定义。
李代数由一个集合\(V\),一个数域\(F\),一个二元运算\([,]\)组成,如果满足下面的条件,则称 \((\mathbb{V}, \mathbb{F},[,])\) 为一个李代数。
李代数满足如下性质:
封闭性
\(\forall X, Y \in \mathbb{V}, 有[X,Y] \in \mathbb{V}\) ,
双线性
\(\forall X, Y,Z \in \mathbb{V}, a,b \in \mathbb{F}\) ,有:
\[[a \boldsymbol{X}+b \boldsymbol{Y}, \boldsymbol{Z}]=a[\boldsymbol{X}, \boldsymbol{Z}]+b[\boldsymbol{Y}, \boldsymbol{Z}], \quad[\boldsymbol{Z}, a \boldsymbol{X}+b \boldsymbol{Y}]=a[\boldsymbol{Z}, \boldsymbol{X}]+b[\boldsymbol{Z}, \boldsymbol{Y}]
\]
自反性
\(\forall \boldsymbol{X} \in \mathbb{V},[\boldsymbol{X}, \boldsymbol{X}]=\mathbf{0}\),
雅可比等价
\(\forall X, Y, Z \in \mathbb{V},[X,[Y, Z]]+[Z,[\boldsymbol{X}, \boldsymbol{Y}]]+[\boldsymbol{Y},[\boldsymbol{Z}, \boldsymbol{X}]]=0\).


三、验证$ \text { so (3) 和 } \mathbf{s e}(3) $属于李代数
这个和第二题类似,对于\(so(3)\)来说,它是定义在\(\mathbb{R^3}\)上的向量,我们记作:\(\phi\),其李括号是
\]
然后安装第二题的思路,以此证明即可。
四、验证(4.20)和(4.21)
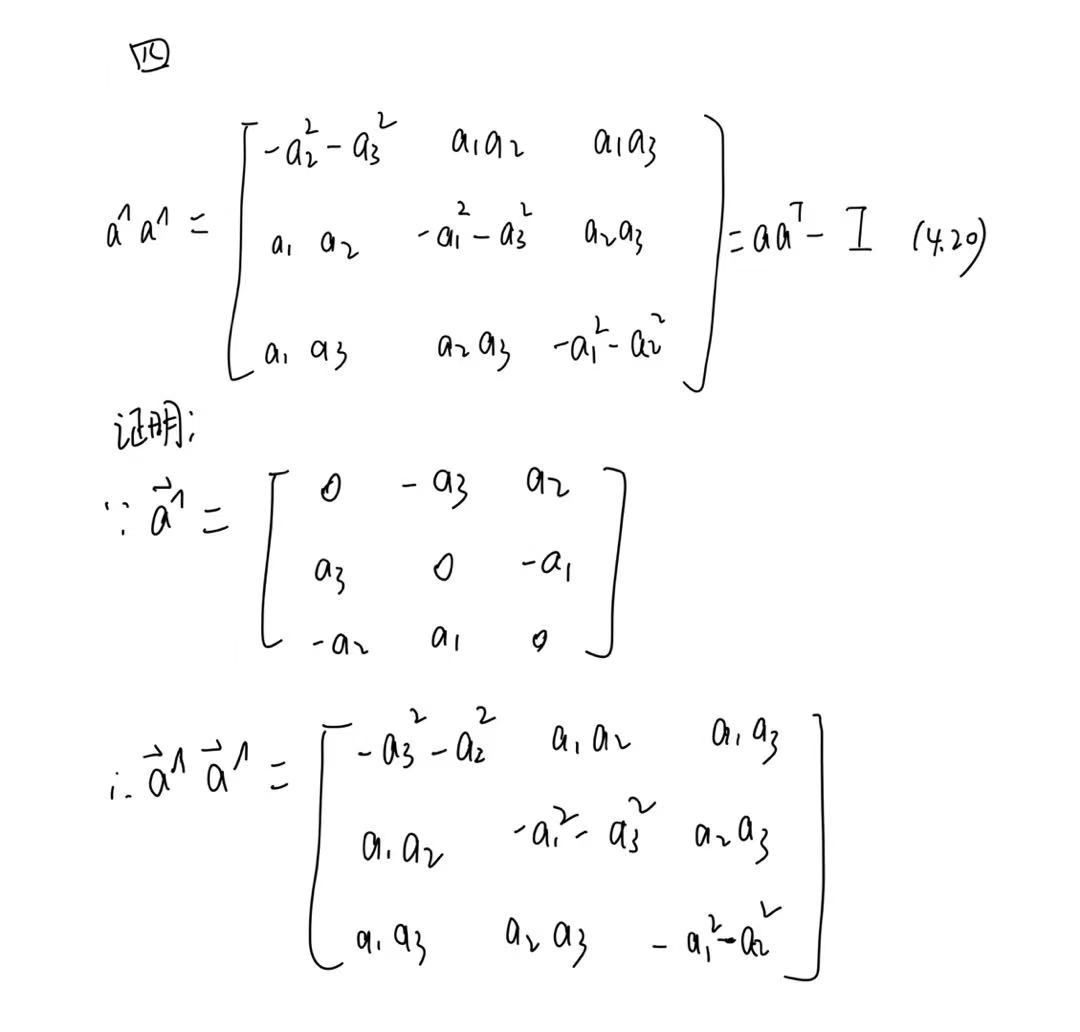
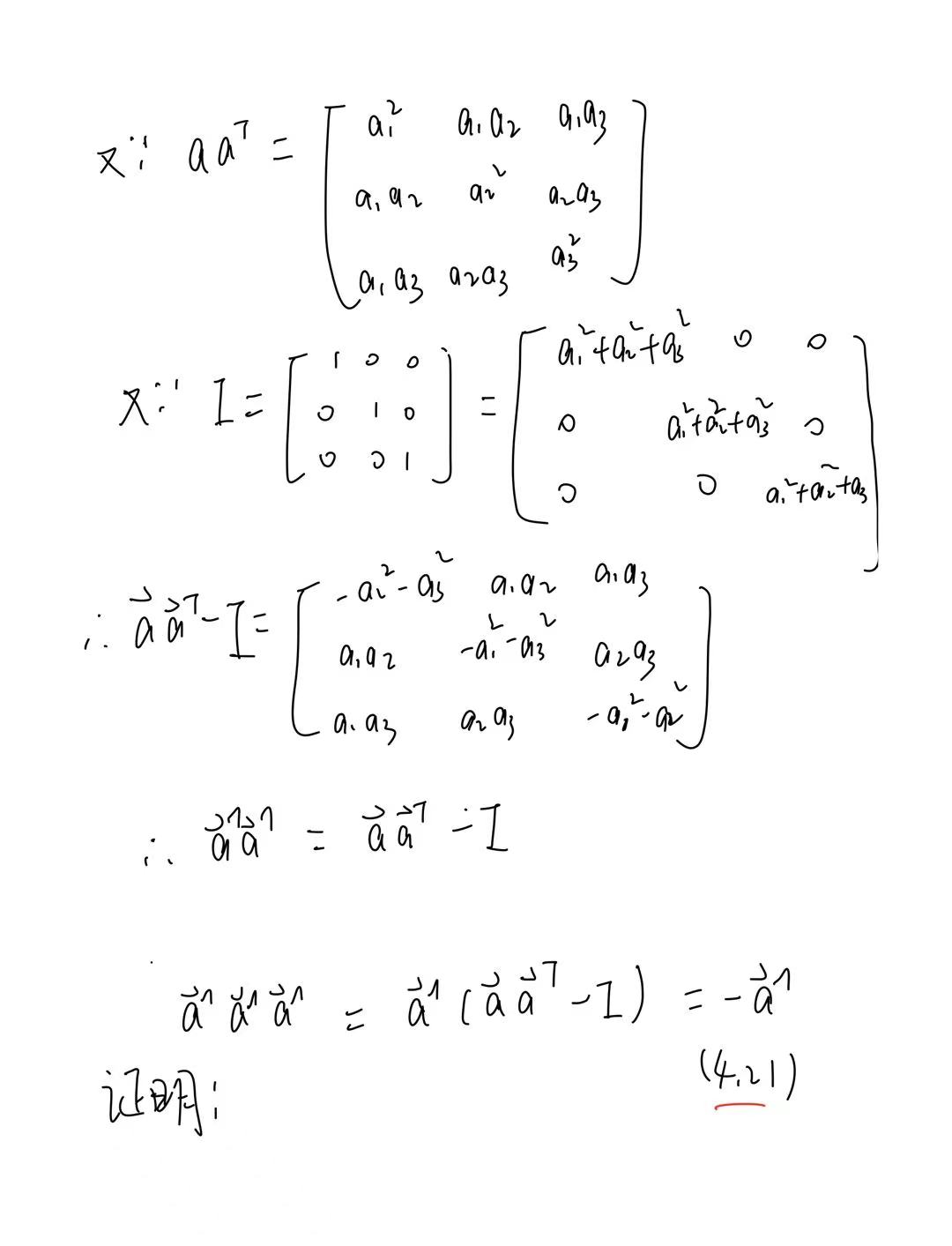

五、证明\(R \hat{p}R^T = (R\hat{p})\)

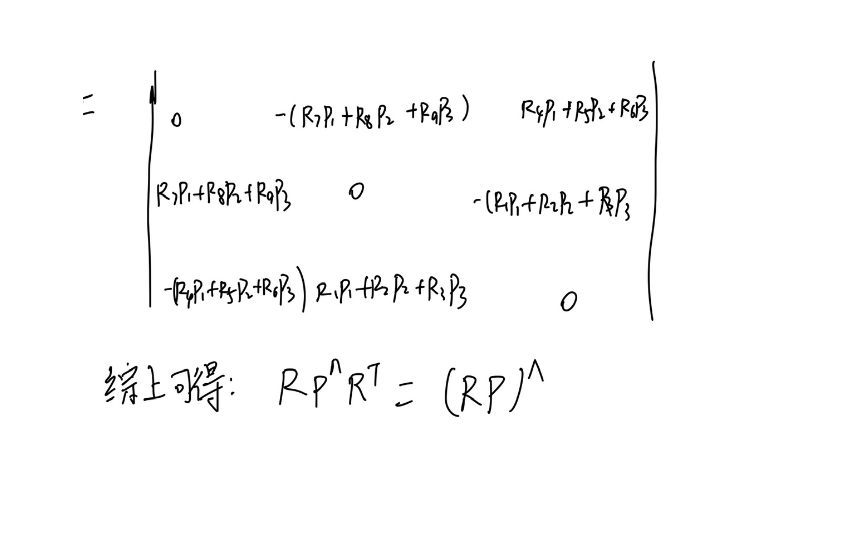
六、\(\text {证明SO(3)的伴随性质 } \operatorname{Rexp}(\hat{p}) R^T=\exp ((\hat{R} p))\)

七、仿照左扰动的推导,推导SO(3)和SE(3)在右扰动下的导数。

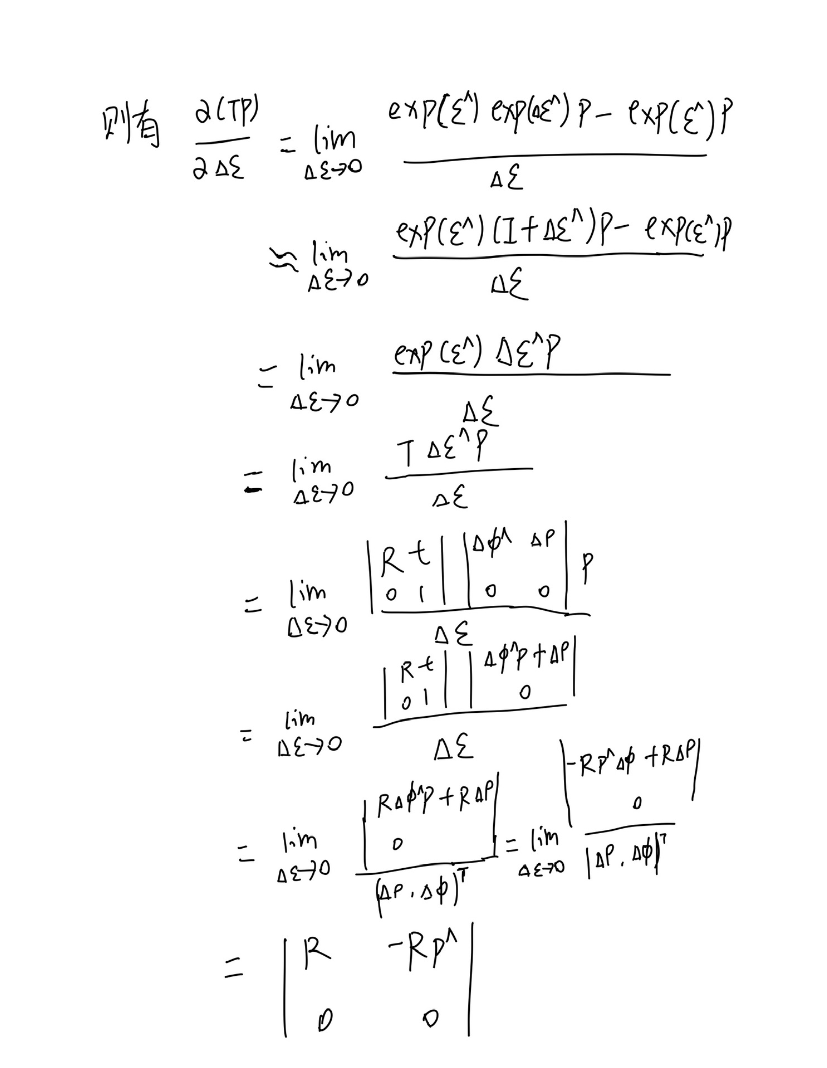
视觉SLAM第四讲李群与李代数习题的更多相关文章
- 《视觉SLAM十四讲》第1讲
目录 一 视觉SLAM 注:原创不易,转载请务必注明原作者和出处,感谢支持! 一 视觉SLAM 什么是视觉SLAM? SLAM是Simultaneous Localization and Mappin ...
- 视觉slam十四讲第七章课后习题6
版权声明:本文为博主原创文章,转载请注明出处: http://www.cnblogs.com/newneul/p/8545450.html 6.在PnP优化中,将第一个相机的观测也考虑进来,程序应如何 ...
- 浅读《视觉SLAM十四讲:从理论到实践》--操作1--初识SLAM
下载<视觉SLAM十四讲:从理论到实践>源码:https://github.com/gaoxiang12/slambook 第二讲:初识SLAM 2.4.2 Hello SLAM(书本P2 ...
- 高博-《视觉SLAM十四讲》
0 讲座 (1)SLAM定义 对比雷达传感器和视觉传感器的优缺点(主要介绍视觉SLAM) 单目:不知道尺度信息 双目:知道尺度信息,但测量范围根据预定的基线相关 RGBD:知道深度信息,但是深度信息对 ...
- 《视觉SLAM十四讲》第2讲
目录 一 视觉SLAM中的传感器 二 经典视觉SLAM框架 三 SLAM问题的数学表述 注:原创不易,转载请务必注明原作者和出处,感谢支持! 本讲主要内容: (1) 视觉SLAM中的传感器 (2) 经 ...
- 视觉slam十四讲第七章课后习题7
版权声明:本文为博主原创文章,转载请注明出处:http://www.cnblogs.com/newneul/p/8544369.html 7.题目要求:在ICP程序中,将空间点也作为优化变量考虑进来 ...
- 视觉SLAM十四讲:从理论到实践 两版 PDF和源码
视觉SLAM十四讲:从理论到实践 第一版电子版PDF 链接:https://pan.baidu.com/s/1SuuSpavo_fj7xqTYtgHBfw提取码:lr4t 源码github链接:htt ...
- 《视觉SLAM十四讲》visual studio 19 + PCL点云创建图像与现实
SLCM真是博大精深.之前简单的学习了OpenCV,主要是是使用python语言,现在学习SLAM需要使用C++,略难,但比起SLAM本身,不值一提. <视觉SLAM十四讲>里面的环境主要 ...
- 高翔《视觉SLAM十四讲》从理论到实践
目录 第1讲 前言:本书讲什么:如何使用本书: 第2讲 初始SLAM:引子-小萝卜的例子:经典视觉SLAM框架:SLAM问题的数学表述:实践-编程基础: 第3讲 三维空间刚体运动 旋转矩阵:实践-Ei ...
- 视觉slam十四讲
对这个的学习一直都在,感觉到了这本书很强大呀!!! ch2---安装ubuntu:安装kdevelop. ch3---安装eigen3---几何模块:安装Pangolin可视化. ch4---安装So ...
随机推荐
- 痛苦调优10小时,我把 Spark 脚本运行时间从15小时缩短到12分钟!
周一我就有个困惑,还写成文章了:如何从 Spark 的 DataFrame 中取出具体某一行,里面提了自己猜想的几种解决方案. 没想到这么快就要面对这个问题了,我用小孩子都听得懂的例子描述一下我在干什 ...
- 优化博客Ⅱ-CDN加速
CDN加速 自从有了第一次博客优化经验,我就越发对优化感兴趣了嘿嘿(✧∇✧). 看着博客首页打开时长为1200ms左右,我又开始琢磨有什么办法能再给网站提提速,让访问时间降低到1000ms以下,这时候 ...
- Solution Set -「AGC 013~015」C~F
目录 「AGC 013C」Ants on a Circle 「AGC 013D」Piling Up ^ 「AGC 013E」Placing Squares ^ 「AGC 013F」Two Faced ...
- Android开发快速入门iOS开发概览
注:本文同步发布于微信公众号:stringwu的互联网杂谈 Android开发快速入门iOS开发概览 1 前言 笔者总结了自己在拥有Android开发的相关基础后入门iOS开发时遇到的点点滴滴给其他想 ...
- CDS标准视图:催款代码 I_DunningKey
视图名称:催款代码 I_DunningKey 视图类型:基础 视图代码: 点击查看代码 @AccessControl.authorizationCheck: #NOT_REQUIRED @EndUse ...
- 分布式事务-XA-DTP-TCC-BASE介绍
前言 数据库事务(简称:事务,Transaction)是指数据库执行过程中的一个逻辑单位,由一个有限的数据库操作序列构成. 事务拥有以下四个特性,习惯上被称为 ACID 特性: 原子性(Atomici ...
- Redis组件的特性,实现一个分布式限流
分布式---基于Redis进行接口IP限流 场景 为了防止我们的接口被人恶意访问,比如有人通过JMeter工具频繁访问我们的接口,导致接口响应变慢甚至崩溃,所以我们需要对一些特定的接口进行IP限流,即 ...
- CentOS扩容boot分区并升级内核
本文作者CVE-柠檬i:https://www.cnblogs.com/CVE-Lemon 前言 由于安装k8s需要升级内核,但我自己的的boot分区只有200M大小,无法安装新内核,所以干脆把swa ...
- Kotlin:【泛型】
- AI编程:如何编写提示词
这是小卷对AI编程工具学习的第2篇文章,今天讲讲如何编写AI编程的提示词,并结合实际功能需求案例来进行开发 1.编写提示词的技巧 好的提示词应该是:目标清晰明确,具有针对性,能引导模型理解问题 下面是 ...
