P8328 [COCI 2021/2022 #5] Usmjeravanj

本题的实际难度和通过数不是相符。

实际思维难度：蓝

代码实现难度：绿

部分1、简化题意

存在两条河流，假设分别叫做① 和 ②。

其中①号河流有 $a$ 座城市， ② 号河流有 $b$ 座城市。

河流方向是从编号小的城市流向编号大的城市，现在准备在两条河流的某些城市上建立 $m$ 座桥，每座桥都是单向的，请给定每座桥的方向，

其中 $0$ 方向代表从河流 ① 上的城市到河流 ② 的城市， $1$ 方向刚好相反。

现在需要使得强连通分量最少，请给出每座桥的具体方向（输出任意一个即可）

比如下图就是一个参考。

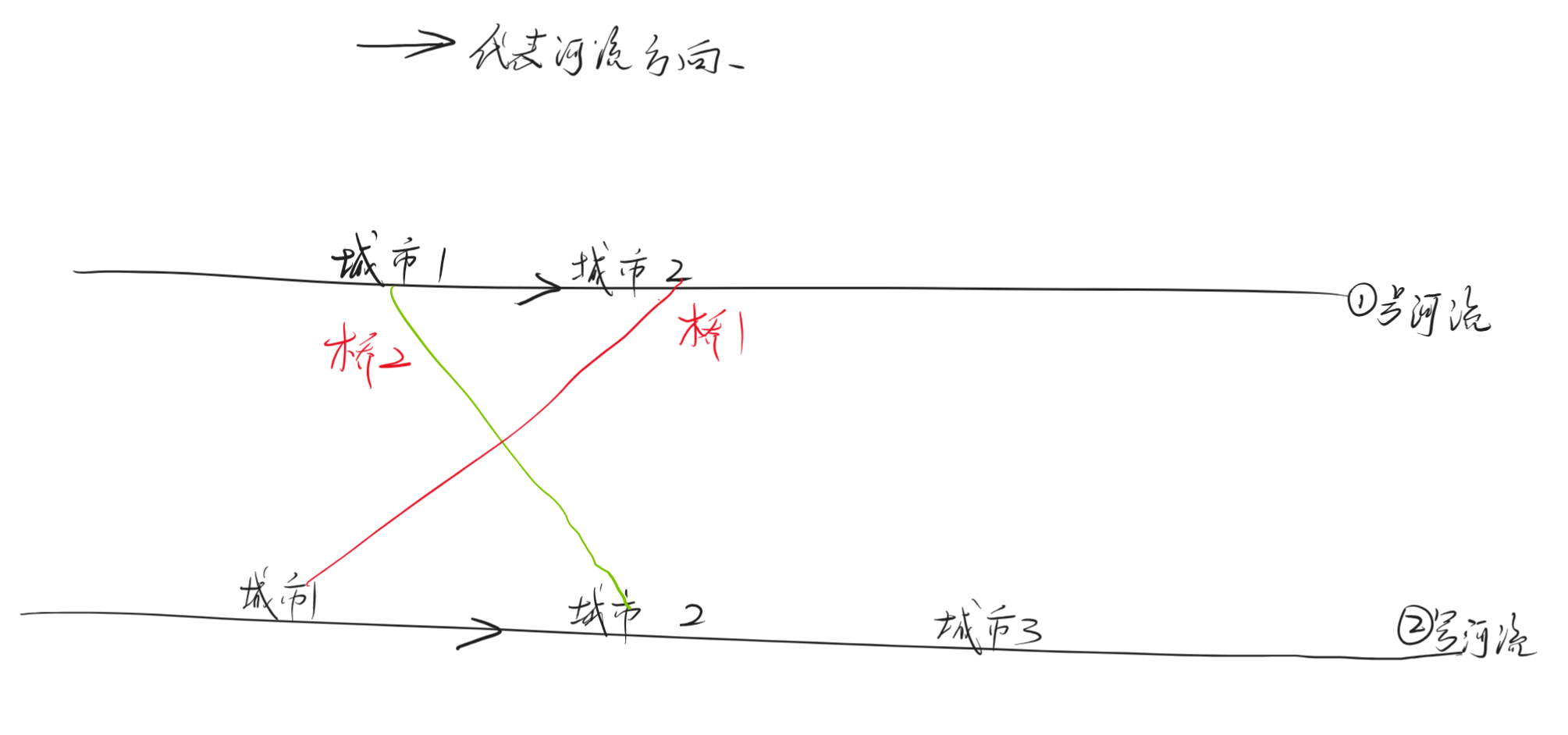
样例一分析：

输入：

输出：

按照下方给定的最优合法方案，是按照下图所示，所有城市都是连通的。

1

1 1 0 0

部分2、思路分析

首先上述的题目跟有向图的连通有关，大概率是强连通分量，如果没有给定边的选择，直接给定方向，直接可以建边获取得到scc。

值得注意的是，①号河流和②号河流的城市编号相同，肯定不可取，所以可以给②号河流加上一个偏移量

比如

add_edge(a[i], b[i] + n);

答案求解已经得到，重点是如何建边？

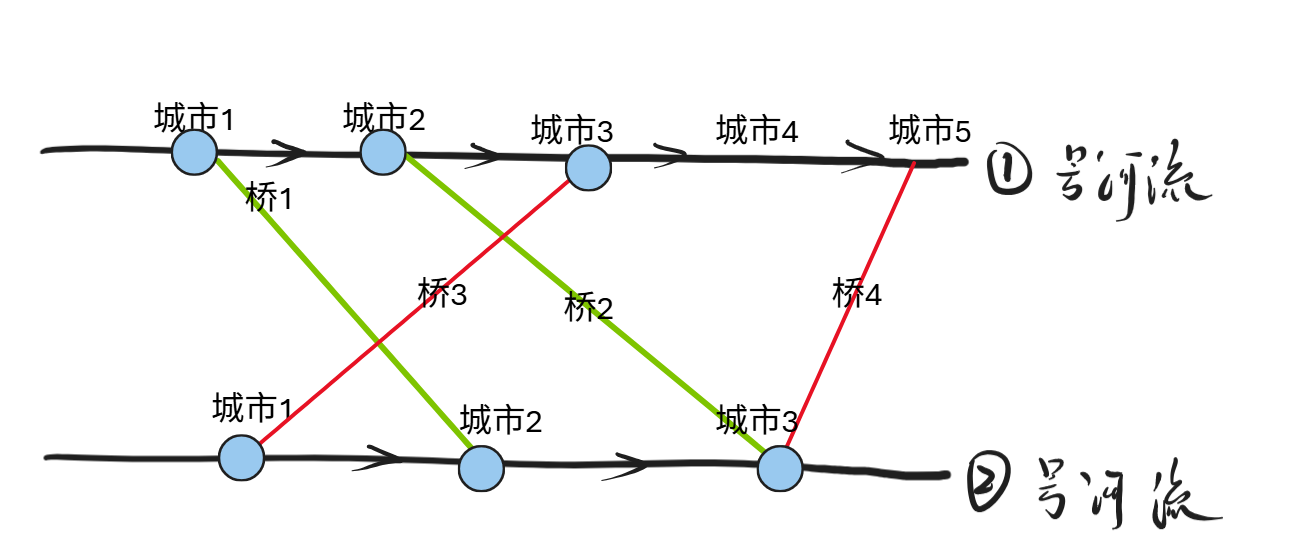
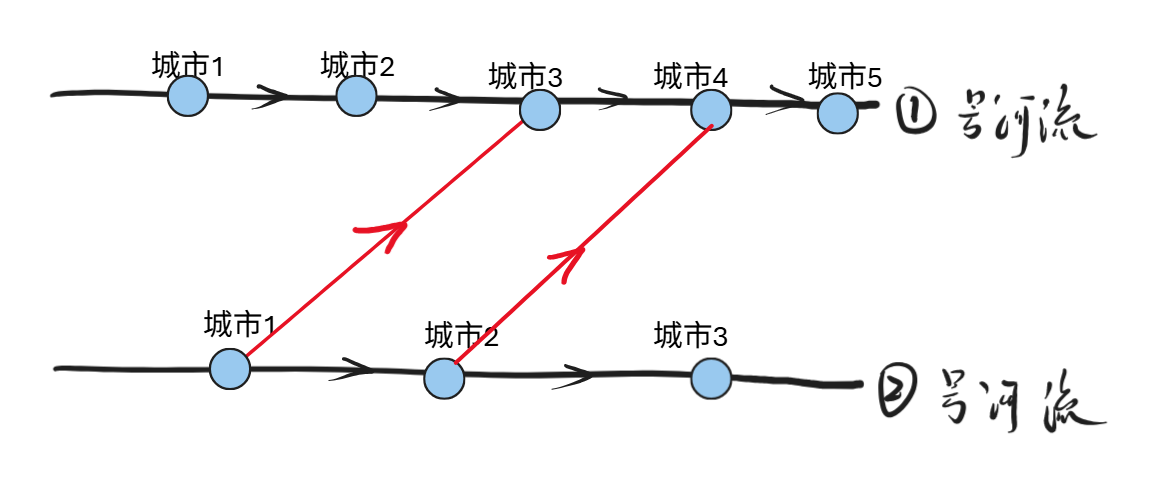
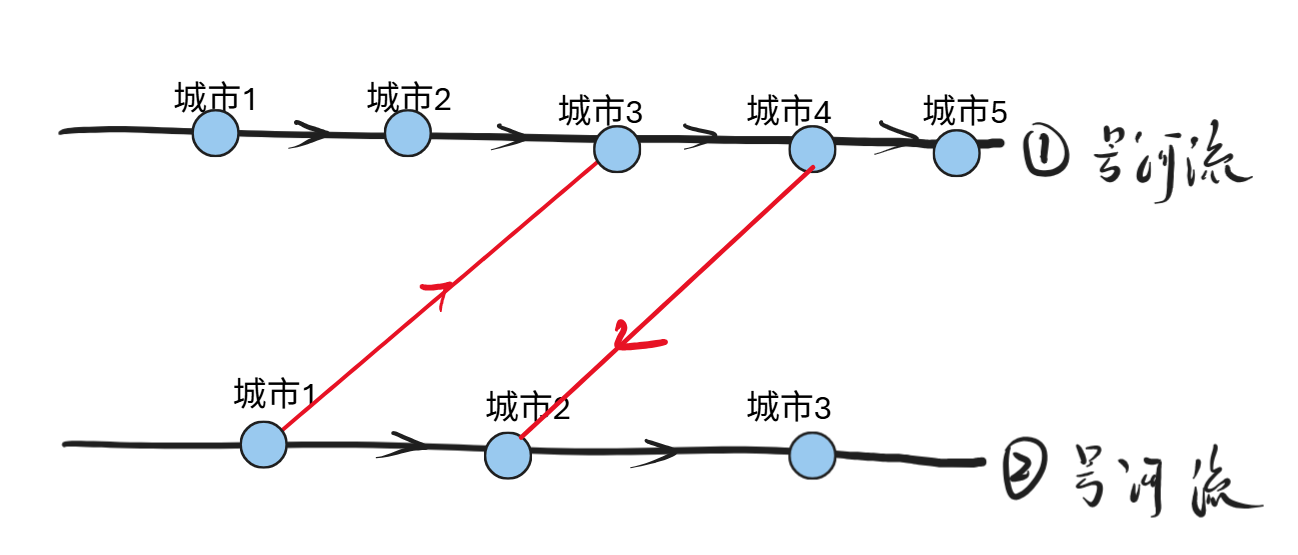
首先考虑的一点是，选定合适的桥的方向，可以减少强连通分量的数量，假设目前只有两座桥，先进行分类讨论：

情况一：两座桥不交叉，并且相同方向

结论：下述四种情况，最终无论情况如何，得到的结果对scc无影响。

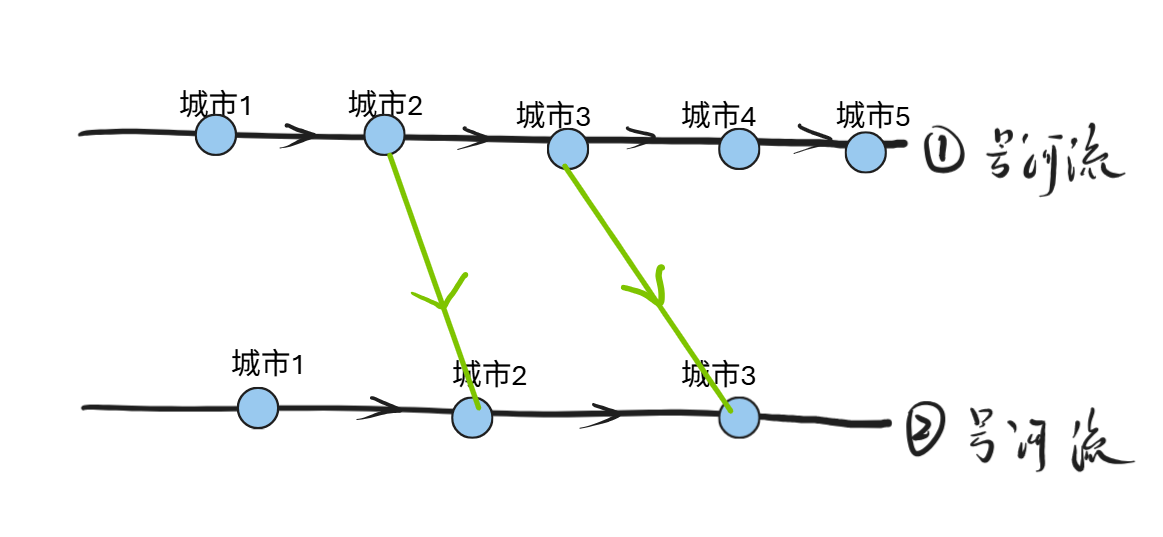
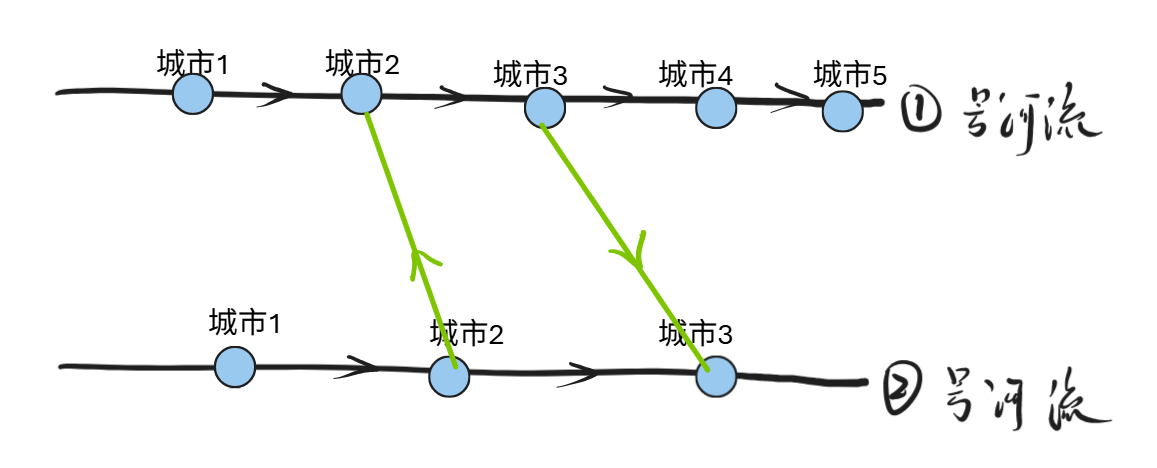
情况二：两座桥不交叉，并且不同方向

结论：下述四种情况，最终无论情况如何，得到的结果对scc无影响。

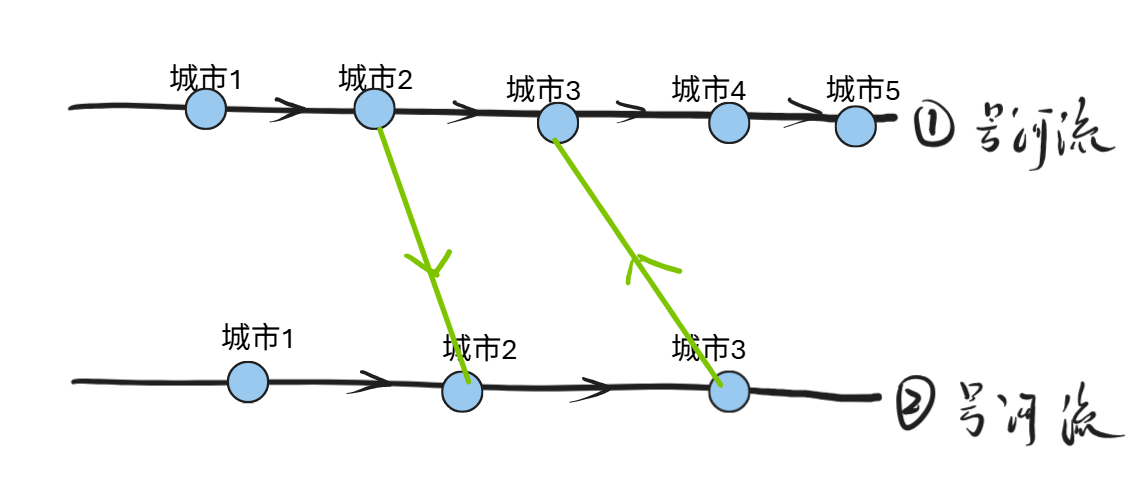
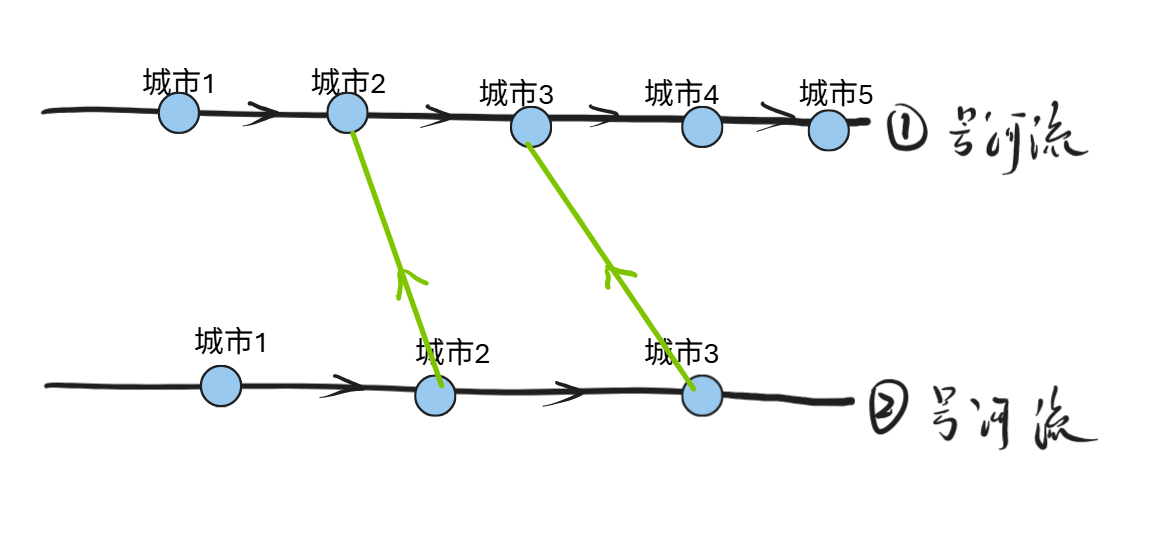
情况三：两座桥交叉，并且相同方向

结论：下述两种情况对scc无影响

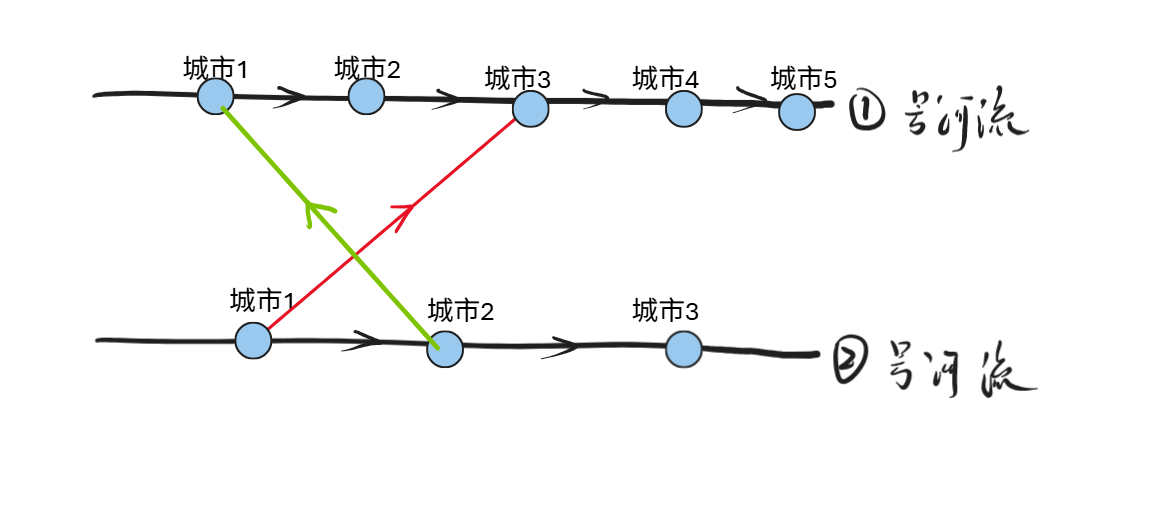
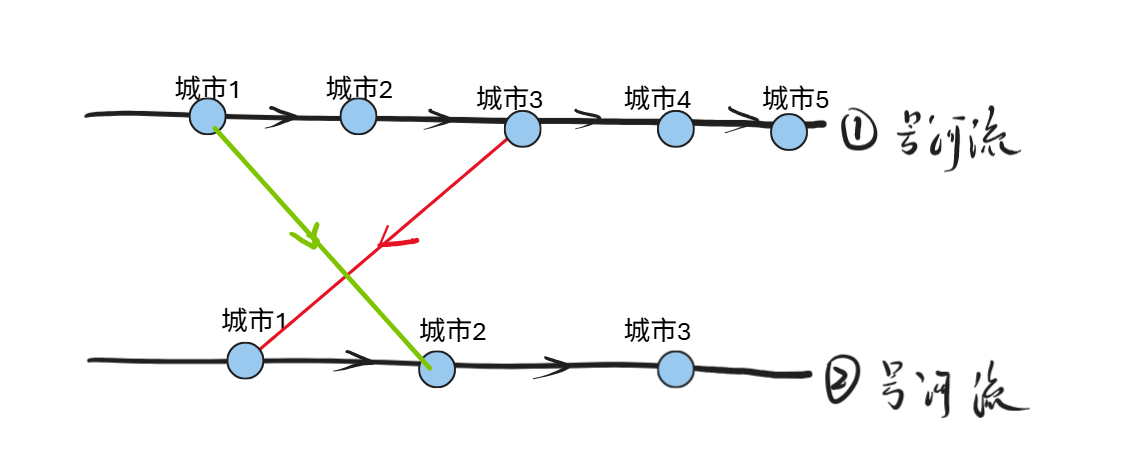
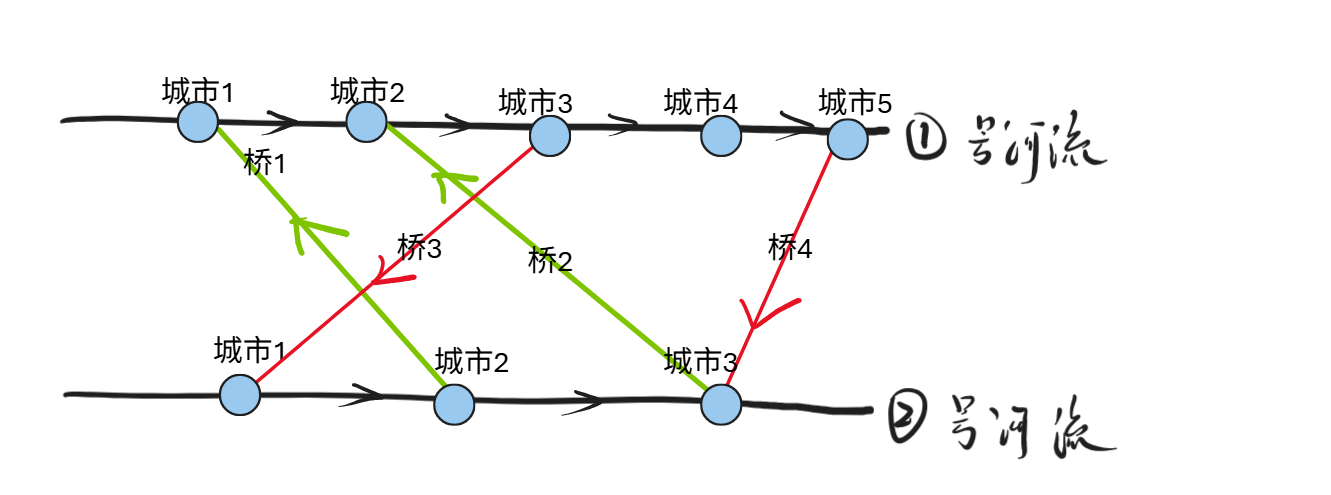
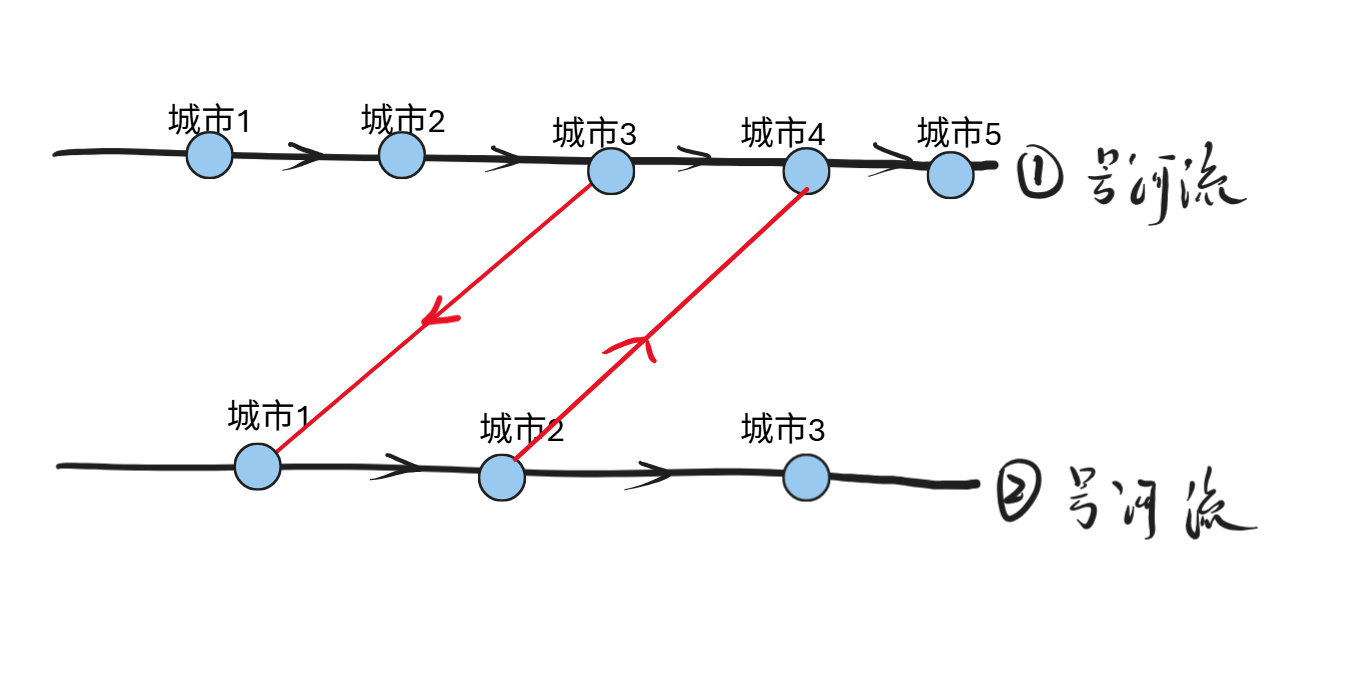
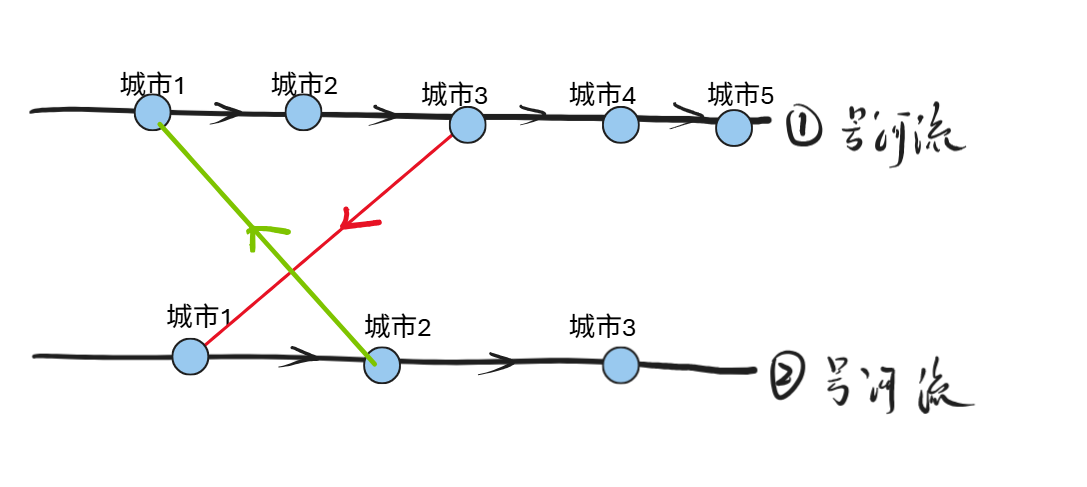
情况四：两座桥交叉，并且不同方向

结论：只有第一张图的方案可以使得scc数量减少，但是第二张图对scc无影响。

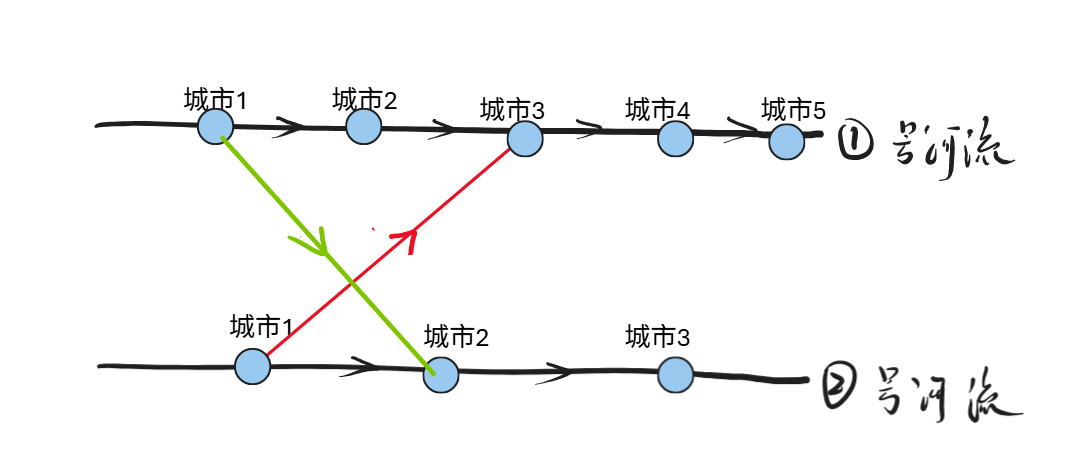
最终结论：所有的建边方向，考虑交叉之后，方向相反的答案（按照下图建边）

部分3、具体实现和代码细节

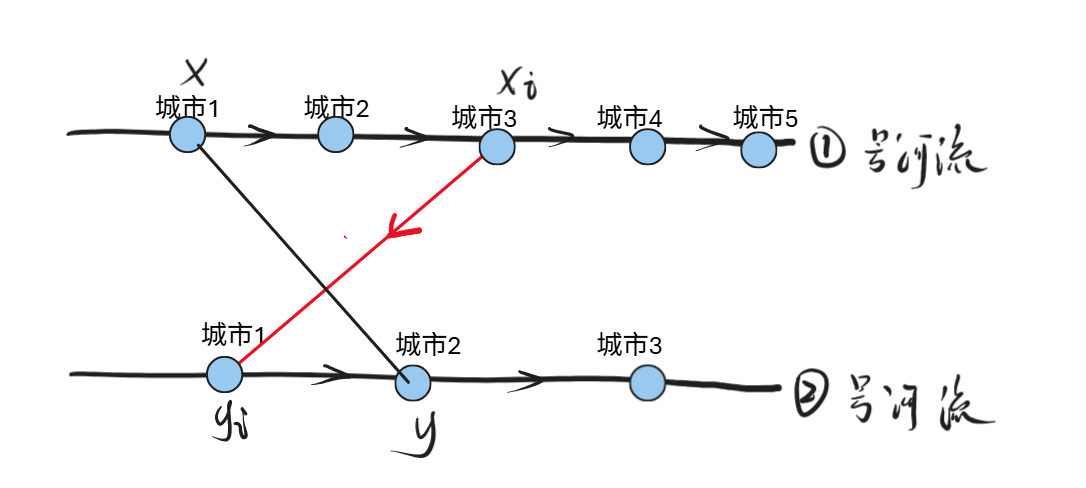
如何判断最终结论，首先假设将所有的桥进行了存储，分别标记为 $x_i$ 和 $y_i$ 。

桥交叉的话，只可能是以下两种选择

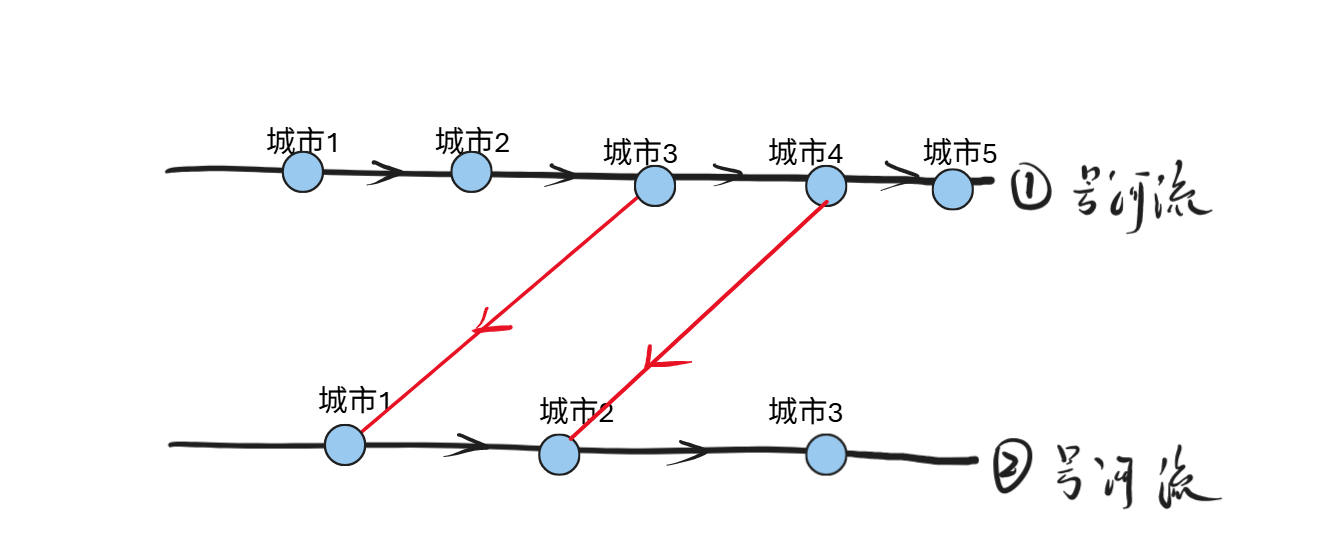
选择1、黑色桥是之前已经选择过的，红色的桥是现在需要控制方向的，此处无论黑色的桥的方向如何，

按照如下图所示的方向，从 $x_i $ 指向 $ y_i$ 一定是最佳的。

判断方式是

$x < x _ i $ 并且 $ y_i < y$

选择2、黑色桥是之后需要选择的，绿色桥是现在需要选择的方向，按照这种方式才可能交叉。

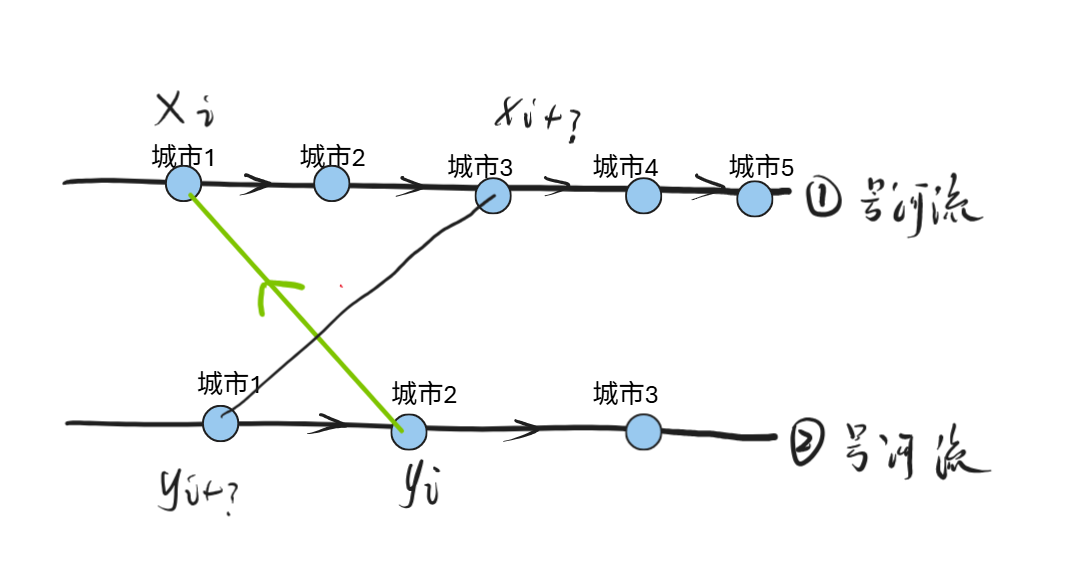
综上：桥的方向选择比较容易确定，考虑桥的选择的优先顺序，首先确立上述的绿色的边，然后确立红色的边会比较方便一些。

另外看到上述的判断方式，二维偏序关系，可以先排序处理为一维偏序。

按照 $x$ 的顺序从小到大，这样我们在选择的时候，桥枚举的时候，①号河流的城市编号非递减，此时比较交叉的时候，下述关系的

$x < x _ i $ 自动满足，另外只需要找到 $ y_i < y$ ，那么如何判断有没有交叉，需要获取 $R = y_{max}$ ，也就是之前选择过的桥的 $y$ 的最大值。

因为我们需要让 $y_i$ （现在枚举的桥）交叉的数量最多，此时的 $y$ (之前出现过的桥) 值越大越好。

说的简单点就是，下方的两座桥，当 $x$ 相等的时候，我们肯定会优先把后面绿色的桥的方向考虑，因为后面的桥可以交叉的数量更多。

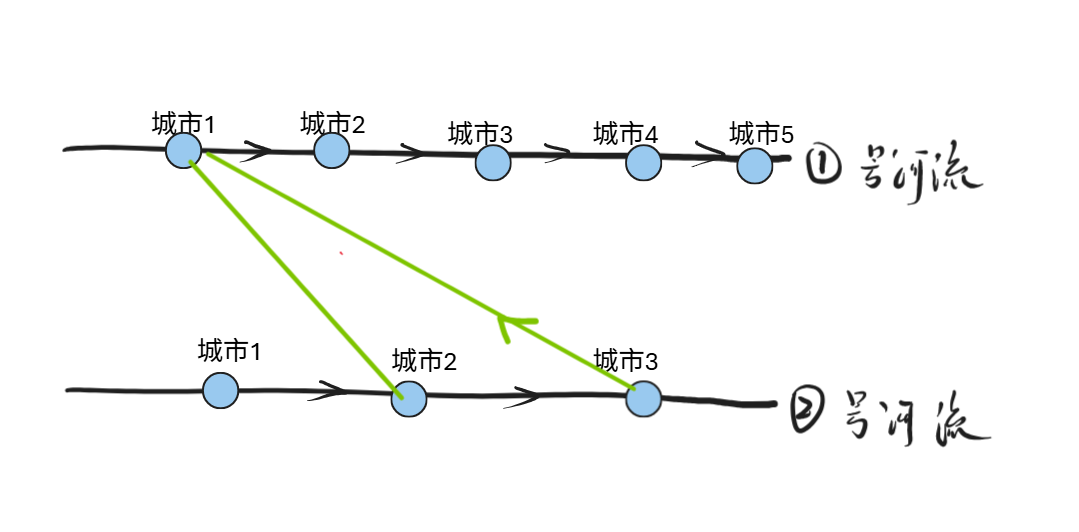
代码实现步骤：

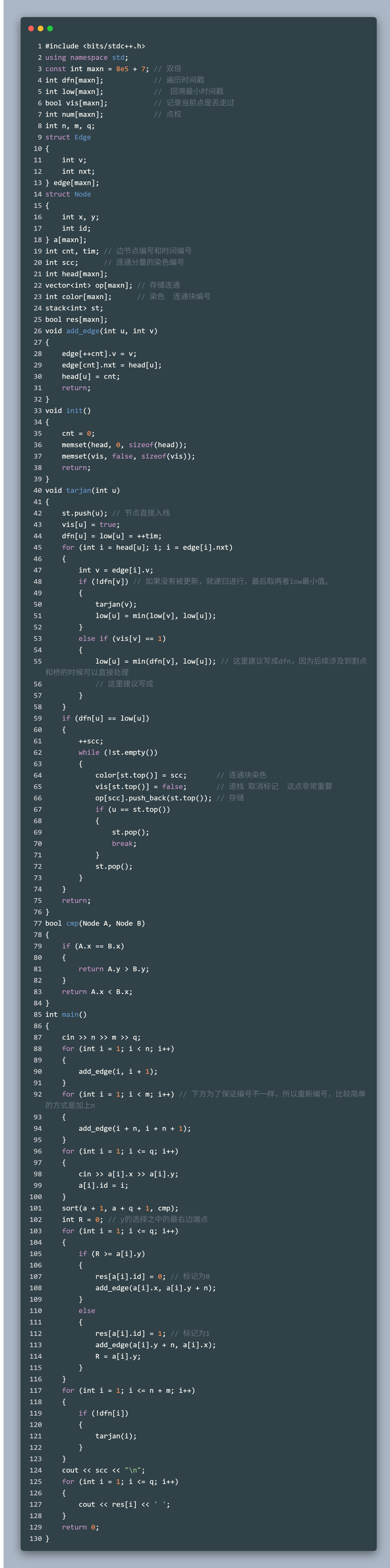
步骤一：按照x作为第一关键词，从小到大排序，按照y作为第二关键词，从大到小排序

步骤二：如果枚举的y[i] <= R,说明有交叉，选定边的方向和上述图之中的红色边一致，也就是0方向；如果枚举的 y[i] > R ，说明没有交叉，但是此时的y更大，需要更新R，此时按照绿色边（选择2）去处理更优，也就是 1 方向。

代码参照：