[题解]（最短路）luogu_P5122 Fine Dining

首先理解这里的美味值相当于给你更多时间让你经过这个草垛的，

也就是在经过草垛时可以给你的时间减少w[i]，这样能否比最短路不慢

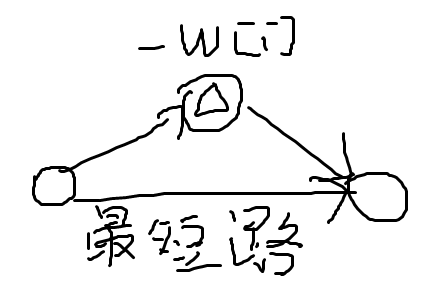
然而我们并不容易知道怎么走才是最好的，所以要想办法避免找这个方案

我们新建一个点，向每个草垛连一个边权为 d[u]-w[u] 的有向边，从这个点跑一次最短路

效果就相当于求了从每个点到这个新点的最短路，而我们看d2[x]的组成，

我们想要的效果是从x出发走到u，减去一个w[u]，再走到n，看能不能更好

而走到u之后不走到n，而是走到这个新点，d2[x]的组成就是从x走到u再加上u点到新点的边权d[u]-w[u]，效果是一样的

这样就很好的避免了找方案的问题

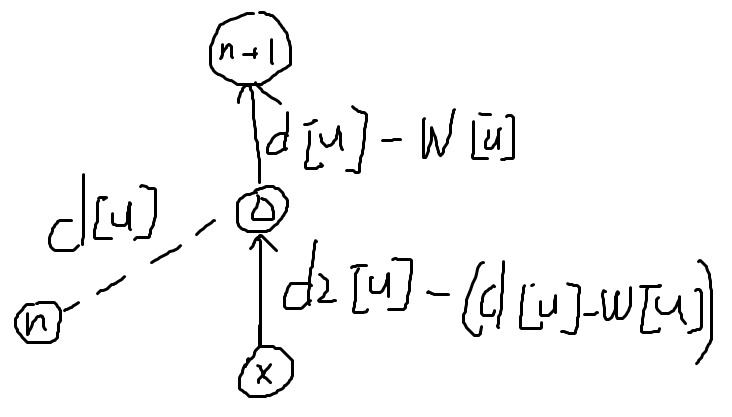
最后比较一下d2[x]和d[x]的大小

#include<bits/stdc++.h>
#define mp make_pair
using namespace std;
const int maxn=;
const int maxm=;
int n,m,k;
struct node{
    int v,w,nxt;
}e[maxm*];
int head[maxn],cnt;
void add(int u,int v,int w){
    e[++cnt].w=w;e[cnt].v=v;e[cnt].nxt=head[u];head[u]=cnt;
}
priority_queue<pair<int,int> >q;
int d[maxn],d2[maxn],v[maxn];
void dij(int s){
    memset(d,0x3f,sizeof(d));
    memset(v,,sizeof(v));
    d[s]=;q.push(mp(,s));
    while(!q.empty()){
        int x=q.top().second;q.pop();
        if(v[x])continue;v[x]=;
        for(int i=head[x];i;i=e[i].nxt){
            int y=e[i].v,z=e[i].w;
            if(d[y]>d[x]+z)
            d[y]=d[x]+z,q.push(mp(-d[y],y));
        }
    }
}
int main(){
    scanf("%d%d%d",&n,&m,&k);
    for(int i=,u,v,w;i<=m;i++){
        scanf("%d%d%d",&u,&v,&w);
        add(u,v,w);add(v,u,w);
    }
    dij(n);
    for(int i=;i<=n;i++)d2[i]=d[i];
    for(int i=,u,w;i<=k;i++){
        scanf("%d%d",&u,&w);
        add(n+,u,d2[u]-w);
    }
    dij(n+);
    for(int i=;i<n;i++)
    if(d2[i]>=d[i])printf("1\n");
    else printf("0\n");
}