洛谷 3275 [SCOI2011]糖果

题目戳这里

N句话题意

有N个人，k个限制，有五种限制

如果X=1， 表示第A个小朋友的糖果必须和第B个小朋友的糖果一样多；

如果X=2， 表示第A个小朋友的糖果必须少于第B个小朋友的糖果；

如果X=3， 表示第A个小朋友的糖果必须不少于第B个小朋友的糖果；

如果X=4， 表示第A个小朋友的糖果必须多于第B个小朋友的糖果；

如果X=5， 表示第A个小朋友的糖果必须不多于第B个小朋友的糖果；

求满足所有要求需要最少的糖果数（每个人至少为1）

**Solution**

一个差分约束题目，然额本蒟蒻还不是很会。首先分析限制条件，很明显2和4，3和5是一样的限制，并且要求最少的糖果数。那么不少于（多于）我们就建0边，而要求少于（多于）我们就建权值为1的边，很明显这样所需要的糖果最少。建好图后我们只需要跑一遍最长路即可。

为什么是最长路呢？看看下面这张图，（也是盗的）。

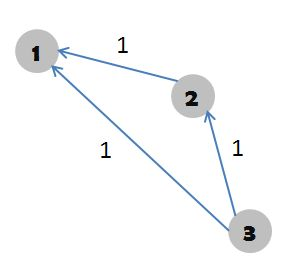
图中dis[1]如果是最短路为1，但很显然1点至少需要两个糖果。（很显然，因为肯定得满足约束最多的条件的情况才是合法的！）。

注：后面0向1→n建边时一定要倒序。

Coding

#include<bits/stdc++.h>
using namespace std;
const int N = 1e6+10;
int head[N],n,m,cnt;
struct limit
{
    int to,next;
    long long w;
}e[N*5];
void add(int x,int y,long long w)
{
    e[++cnt].to=y,e[cnt].next=head[x],e[cnt].w=w;
    head[x]=cnt;
}
int dis[N],tot[N];
long long vis[N];
queue<int> q;
bool SPFA()
{
    q.push(0);
    dis[0]=0;
    vis[0]=1;
    while(!q.empty())
    {
        int u=q.front();
        q.pop();
        vis[u]=0;
        tot[u]++;
        if(tot[u]==n-1) {cout<<-1; return 0;}
        for(int i=head[u];i;i=e[i].next)
        {
            int v=e[i].to;
            if(dis[u]+e[i].w>dis[v])
            {
                dis[v]=dis[u]+e[i].w;
                if(!vis[v]) q.push(v),vis[v]=1;
            }
        }
    }
    return 1;
}
int main()
{
    cin>>n>>m;
    for(int i=1;i<=m;i++)
    {
        int x,y,opt;
        scanf("%d%d%d",&opt,&x,&y);
        if(opt==1) add(x,y,0),add(y,x,0);
        if(opt==2)
        {
            if(x==y) {cout<<-1; return 0;}
            add(x,y,1);
        }
        if(opt==3)	add(y,x,0);
        if(opt==4)
        {
            if(x==y) {cout<<-1; return 0;}
            add(y,x,1);
        }
        if(opt==5)	add(x,y,0);
    }
    for(int i=n;i;i--) add(0,i,1);
    if(!SPFA()) return 0;
    long long ans=0;
    for(int i=1;i<=n;i++)
    ans+=dis[i];
    cout<<ans;
    return 0;
}