OO第一单元总结——多项式求导

　　第一次作业分析

1.程序结构分析

　　类图：

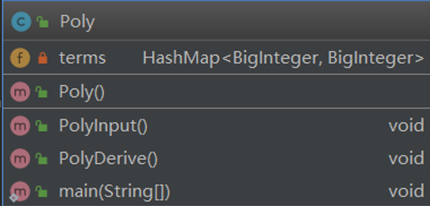
　　好吧，这一次基本上完全是在面向过程编程，没有看出来任何的面向对象的特性。

　　复杂度：

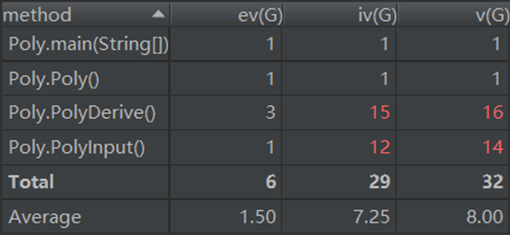
　　可以看到模块间的相互耦合度很高，PolyDerive方法的非结构化程度也不够理想，是非常不合格的面向对象程序。

2.正则表达式

　　从带符号整数到项到多项式一步步地写出对应的正则表达式：

　　　　符号　　　　String signStrPat = "(?:\\+|-)";
　　　　带符号整数   String intStrPat = "(?:\\+|-)?\\d+";
　　　　项 　　　　  String termStrPat = "(?:(?:(?:(?:(?:\\+|-)?\\d+\\s*\\*)|\\+|-)?"
　　　　　　　　　　　　+ "\\s*x\\s*(?:\\^\\s*(?:\\+|-)?\\d+)?)|(?:(?:\\+|-)?\\d+))";
　　　　多项式 　　  String polyStrPat = "^\\s*" + signStrPat + "?\\s*" + termStrPat 
　　　　　　　　　　　　+ "(?:\\s*" + signStrPat + "\\s*" + termStrPat + "\\s*)*+$";

3.总结

　　虽然程序没有bug，但是第一次作业只能说是java编程，不能叫面向对象程序设计，写的很烂，不过熟悉了java基本语法和java正则表达式。

　　第二次作业分析

1.程序结构分析

　　类图：

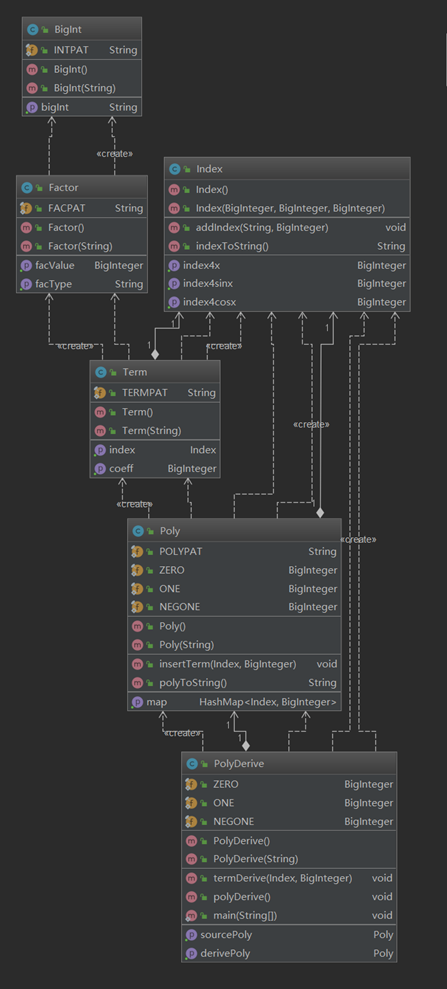
　　这一次采用了面向对象的思想，定义了因子、项和多项式类，但是不够熟练，在架构上存在不小的问题：

　　BigInt类其实完全没有必要，Index类和Term类功能严重重叠，求导操作全部集中在PolyDerive等等等等。

　　这些都是在架构上很丑陋的一些设计，也导致了无法进行三角函数的化简，以及下一次作业需要再次重构。

　　复杂度：

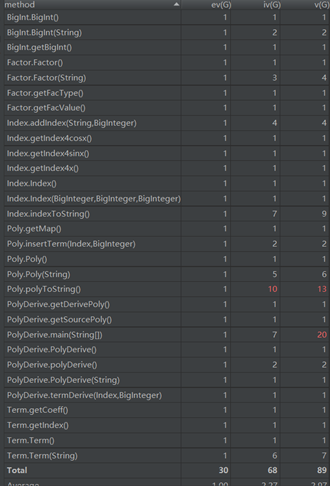
　　部分模块的耦合度还是比较高，勉强合格吧。

2.正则表达式

　　同样采用层次化的写法，而且将每一个类对应的正则表达式用public static final修饰写在了每个类的内部：

　　　　带符号整数　　public static final String INTPAT = "(?:\\+|-)?\\d+";

　　　　因子　　  　　 public static final String FACPAT = "(?:(?:(?:x|(?:(?:sin|cos)\\s*\\(\\s*x\\s*\\)))"

　　　　　　　　　　　　+ "(?:\\s*\\^\\s*" + BigInt.INTPAT + ")?)|" + BigInt.INTPAT + ")";

　　　　项 　　　　　  public static final String TERMPAT = "(?:(?:\\+|-)?\\s*" + Factor.FACPAT

　　　　　　　　　　　　+ "(?:\\s*\\*\\s*" + Factor.FACPAT + ")*+)";

　　　　多项式 　　　  public static final String POLYPAT = "(?:\\+|-)?\\s*" + Term.TERMPAT

　　　　　　　　　　　　+ "(\\s*[\\+-]\\s*" + Term.TERMPAT + ")*+";

3.总结

　　没有bug，但是依旧丑陋。

　　第三次作业分析

1.程序结构分析

　　类图：

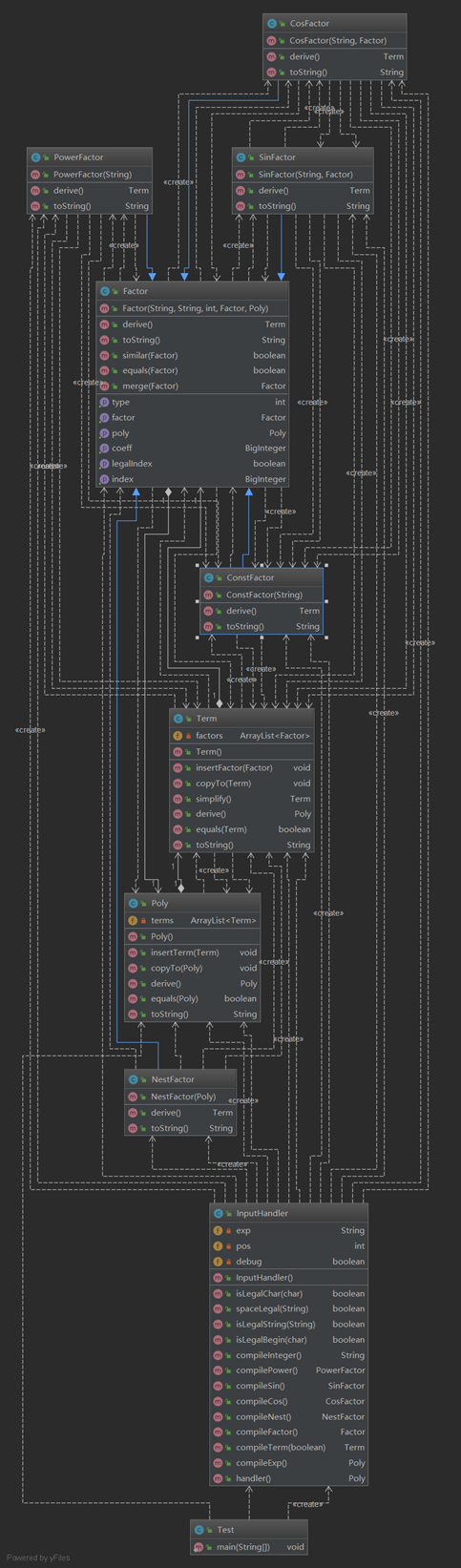
　　这次作业的因子有常数、幂函数、三角函数、表达式因子，我的思路就是构造这些因子的类继承总的因子类，并且构造项和表达式类，然后用递归下降分析法处理输入，构造相应的对象。　　

　　化简（simplify方法）时调用类内similar方法和equals方法进行判断。

　　复杂度：

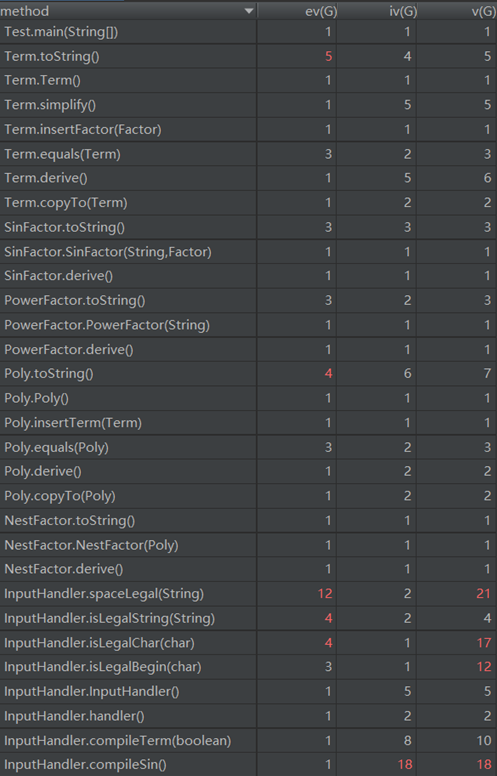
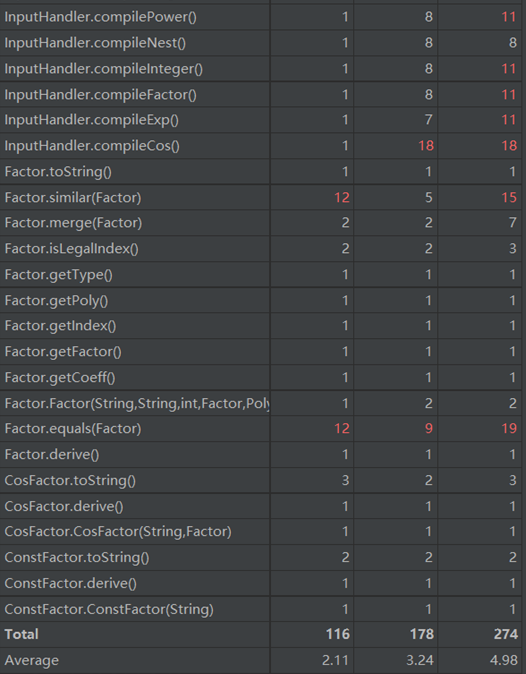
　　由于sin和cos三角函数因子内部有因子，所以耦合度过高。另外，similar方法和重写的equals方法因为要遍历比较所以复杂度过高。这也导致了公测时三个样例运行时间过长。

2.输入处理

　　由于引入了表达式因子，所以没有想出来怎么用java正则表达式来对整体表达式进行识别。

　　但是联系到编译原理课上学过的词法分析和语法分析，可以很自然地用自动机和递归下降分析法来处理输入。

　　但是这种写法最终导致程序的复杂度很高，而且遇到深层次的括号嵌套时会构造很多冗余的、没有必要的对象（例如"((((x))))",会调用五次表达式分析，构造五个表达式、项、因子）。

3.总结

　　这次作业公测出现了三个测试样例运行时间过长而判错，由于自己测试时未进行多重括号嵌套的测试，事先没有发现这个问题。

　　收获与反思

　　经过这三次作业已经基本理解了面向对象的思想，但是在一些细节上还不够熟练，需要多加雕琢。

　　在架构上一定要多花心思，在测试上一定要下功夫。