bzoj1997 Planar

题目链接

思路

首先以那个环为框架，把所有的边连出来。如果有两条边相交，那么就把其中一条放到环外面去。

如图：

\((1,3)\)与\((2,5)相交，\)(1,4)\(与\)(2,5)相交。所以我们把\((2,5)\)这条边放到外面去。

就成了这样

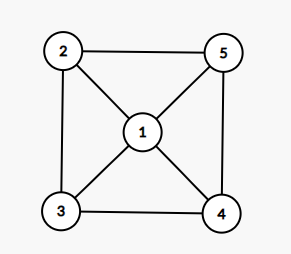
就不会有边相交了。

显然如果两条边在环内相交，那么全部挪到环外也会相交。所以只要是相交的两条边必定是一个在环内，一个在环外。

然后就是2-sat模型了。

坑点。。。

犯了一些很zz的错误。

1.如果边的数量>点的数量乘3-6，即\((m > n \times 3 - 6)\)，可以证明必定无解。这个需要判断掉。

2.没错，这个bug我调了很久233。。。

4.特判的地方要放到全部数据读入之后。。。也调了很久(好zz啊啊啊)

代码

/*
* @Author: wxyww
* @Date:   2019-04-27 19:06:04
* @Last Modified time: 2019-04-27 21:28:17
*/
#include<cstdio>
#include<iostream>
#include<cstdlib>
#include<cstring>
#include<algorithm>
#include<queue>
#include<vector>
#include<ctime>
using namespace std;
typedef long long ll;
const int M = 300010;
#define pi pair<int,int>
ll read() {
    ll x=0,f=1;char c=getchar();
    while(c<'0'||c>'9') {
        if(c=='-') f=-1;
        c=getchar();
    }
    while(c>='0'&&c<='9') {
        x=x*10+c-'0';
        c=getchar();
    }
    return x*f;
}
struct node {
    int v,nxt;
}e[M];
int head[M],ejs;
void add(int u,int v) {
    e[++ejs].v = v;e[ejs].nxt = head[u];head[u] = ejs;
}
int n,m,pos[M];
pi tmp[M];
bool pd(int l,int r,int L,int R) {
    if(l > r) swap(l,r);if(L > R) swap(L,R);
    if((l <= L && r >= R) || (L <= l && R >= r)) return 0;
    if(l >= R || L >= r) return 0;
    return 1;
}
int tot,vis[M],coljs,sta[M],col[M],top,dfn[M],low[M];
void tarjan(int u) {
    dfn[u] = low[u] = ++tot;
    sta[++top] = u;vis[u] = 1;
    for(int i = head[u];i;i = e[i].nxt) {
        int v = e[i].v;
        if(!dfn[v]) {
            tarjan(v);
            low[u] = min(low[u],low[v]);
        }
        else if(vis[v]) low[u] = min(low[u],low[v]);
    }
    if(low[u] == dfn[u]) {
        ++coljs;
        do {
            int x = sta[top--];
            col[x] = coljs;
            vis[x] = 0;
        }while(sta[top + 1] != u);
    }
}
int main() {
    int T = read();
    while(T--) {
        memset(head,0,sizeof(head));
        ejs = 0;
        memset(pos,0,sizeof(pos));
        coljs = 0;memset(col,0,sizeof(col));
        memset(dfn,0,sizeof(dfn));memset(low,0,sizeof(low));
        tot = 0;top = 0;
        n = read(),m = read();
        for(int i = 1;i <= m;++i) tmp[i].first = read(),tmp[i].second = read();
        for(int i = 1;i <= n;++i) pos[read()] = i;
        if(m > 3 * n - 6) {
            puts("NO");continue;
        }
        for(int i = 1;i <= m;++i)
            for(int j = i + 1;j <= m;++j)
                if(pd(pos[tmp[i].first],pos[tmp[i].second],pos[tmp[j].first],pos[tmp[j].second]))
                    add(i,j + m),add(i + m,j),add(j,i + m),add(j + m,i);
        for(int i = 1;i <= m + m;++i) if(!dfn[i]) tarjan(i);
        int bz = 0;
        for(int i = 1;i <= m;++i) if(col[i] == col[i + m]) bz = 1;
        if(bz) puts("NO");else puts("YES");
    }
    return 0;
}