四元数 Quaternion
最近在重写自己游戏引擎的场景管理模块,重温了一下有关四元数的一些知识,在此做一下简单的笔记。
四元数可以用来准确地描述三维矢量的旋转,并且可以有效地表达多个旋转操作的叠加,因此在三维游戏引擎的场景管理模块中,四元数具有很重要的意义。
本文为大便一箩筐的原创内容,转载请注明出处,谢谢:http://www.cnblogs.com/dbylk/
一、定义
形如A = ai + bj + ck + d的复数称为四元数,其中i、j、k为虚数(称为四元数的基元),a、b、c、d为实数。
二、常见性质
1. i2 = j2 = k2 = -1
2. ij = k jk = i ki = j
3. ij = –ji jk = –kj ki = -ki
4. ii* = 1 i* = –i 即i*与i共轭,j、k同理
5. 四元数的乘法运算满足结合律与分配律,不满足交换律
6. 将四元数虚部看作三维矢量,则两个四元数的矢量部分乘积为αβ = -α•β +α×β,令四元数A = α + d1,B = β + d2,则
AB = -α•β +α×β + d2α + d1β + d1d2 = (d1a2 – c1b2 + b1c2 + a1d2) i
+ (c1a2 + d1b2 – a1c2 + b1d2) j
+ (-b1a2 + a1b2 + d1c2 + c1d2) k
– a1a2 – b1b2 – c1c2 + d1d2
7. (AB)* = B*A*
8. 定义四元数 A = ai + bj + ck + d 的范数为:||A|| = a2 + b2 + c2 + d2 ,模为:|A| = sqrt(a2 + b2 + c2 + d2)
9. 定义四元数A的逆为: A-1 = A* / ||A||
10. A-m = (A-1)m = (Am)-1
三、使用四元数表述矢量旋转
假设矢量α绕转轴e = (xe,ye,ze)旋转θ角得到β,则:
β = uαu-1
其中:
u = e sin(θ/2) + cos(θ/2)
u-1 = u* = - e sin(θ/2) + cos(θ/2)
因此,我们可以使用四元数u = (x,y,z,w)表示坐标旋转,其中:
x = sin(θ/2) xe
y = sin(θ/2) ye
z = sin(θ/2) ze
w = cos(θ/2)
四、使用矩阵表示坐标旋转
假设旋转轴为a = (xa,ya,za),旋转角为α,则旋转矩阵如下:
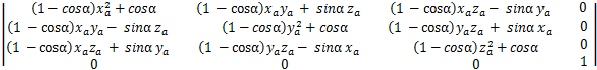
五、四元数与旋转矩阵的转化
根据半角公式:
sinα = 2sin(α/2)•cos(α/2)
cosα = cos2(α/2) - sin2(α/2)
cos2(α/2) = (1 +cosα)/2
sin2(α/2) = (1 -cosα)/2
四元数转化为旋转矩阵可表示如下:
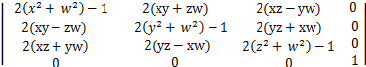
四元数 Quaternion的更多相关文章
- 学习和研究下unity3d的四元数 Quaternion
学习和研究下unity3d的四元数 Quaternion 今天准备学习和研究下unity3d的四元数 Quaternion 四元数在电脑图形学中用于表示物体的旋转,在unity中由x,y,z,w 表示 ...
- unity3d的四元数 Quaternion
原地址:http://www.cnblogs.com/88999660/archive/2013/04/02/2995074.html 今天准备学习和研究下unity3d的四元数 Quaternion ...
- 四元数Quaternion的基本运算
技术背景 在前面一篇文章中我们介绍了欧拉角死锁问题的一些产生背景,还有基于四元数的求解方案.四元数这个概念虽然重要,但是很少会在通识教育课程中涉及到,更多的是一些图形学或者是工程学当中才会进行讲解.本 ...
- 四元数quaternion
四元数的简单方法运用四元数在Unity3D中的作用就是拿来表示旋转. AngleAxis 创建一个旋转,绕着某个轴旋转,返回结果是一个四元数. 跟ToAngleAxis实现的是相反的功能. Angle ...
- [Unity Quaternion]四元数Quaternion的计算方式
什么是Quaternion四元数 1843年,William Rowan Hamilton发明了四元数,但直到1985年才有一个叫Ken Shoemake的人将四元数引入计算机图形学处理领域.四元数在 ...
- 【Unity编程】四元数(Quaternion)与欧拉角
版权声明:本文为博主原创文章,欢迎转载.请保留博主链接:http://blog.csdn.net/andrewfan 欧拉旋转.四元数.矩阵旋转之间的差异 除了欧拉旋转以外,还有两种表示旋转的方式:矩 ...
- 【转】【Unity】四元数(Quaternion)和旋转
http://blog.csdn.net/candycat1992/article/details/41254799
- 四元数和旋转(Quaternion & rotation)
四元数和旋转(Quaternion & rotation) 本篇文章主要讲述3D空间中的旋转和四元数之间的关系.其中会涉及到矩阵.向量运算,旋转矩阵,四元数,旋转的四元数表示,四元数表示的旋转 ...
- 【Unity编程】Unity中关于四元数的API详解
本文为博主原创文章,欢迎转载,请保留出处:http://blog.csdn.net/andrewfan Unity中关于四元数的API详解 Quaternion类 Quaternion(四元数)用于计 ...
随机推荐
- Leetcode 236
思路:1.如果p或q就是根节点,那么LCA=p或q,返回根节点(递归出口) 2.分治 2.1 Divide:分别计算左字树和右子树的LCA 2.2 Conquer:如果左字树和右子树的计算结果均不为空 ...
- XDU 1109
#include<stdio.h> #define N 10007 #define maxn 1000005 int dp[maxn]; int main() { dp[]=,dp[]=, ...
- npm使用淘宝镜像
淘宝 npm 地址: http://npm.taobao.org/ 如何使用 有很多方法来配置npm的registry地址,下面根据不同情境列出几种比较常用的方法.以淘宝npm镜像举例: 1.临时使用 ...
- html-4, form 表单 输入、传文件、单选、多选、下拉菜单、文本描述、重置、submit、按钮限制输入
<!-- form HTTP协议 action:提交的服务器网址 method:get(默认)| post(应用:登录注册.上传文件) 页面中的a img link 默认是get请求 input ...
- spark examples 导入idea并测试
记录下自己使用idea导入spark examples项目的过程. spark examples 项目可以给我们提供很多有益的参考,经常看看这些代码有助于提高我们写scala代码的水平. 只导入spa ...
- 【Q2D】 2048设计
主要组件 1: GameDirector ,负责胜利.失败.载入上次成绩等 2: Grid, 表格类,负责管理tile二维数组 3: Tile 元素类,就是界面上移动的砖块了 4: InputHelp ...
- 【1】Kali Linux的安装及配置
爱生活就得够GEEK. ---------------------------------------------------------------完美的分割线------------------- ...
- netty11---管道
客户端: package com.server; import java.net.Socket; public class Client { public static void main(Strin ...
- .NET BETWEEN方法
Between 值范围比较 可以判断一个值是否落在区间范围值中. public static bool Between<T>(this T me, T lower, T upper) wh ...
- 20145215刘俊谦实验五 Java网络编程及安全
实验内容 掌握Socket程序的编写: 掌握密码技术的使用: 设计安全传输系统. 实验步骤 本次实验由两人组队完成,20145321曾子誉是我本次实验的搭档,链接为:http://www.cnblog ...
