ajax 上传读取excel

$("#btnImport").click(function () {
$("#File").click()
})///委托

$("#File").change(function () {//选择文件改变事件
var formdata = new FormData();
var fileObj = document.getElementById("File").files;
for (var i = 0; i < fileObj.length; i++)
formdata.append("file" + i, fileObj[i]);
$.ajax({
url: "/FacultyStuManage/Uploading",
type: 'POST',
dataType: 'json',
data: formdata,

/**
*必须false才会自动加上正确的Content-Type
*/
contentType: false,
/**
* 必须false才会避开jQuery对 formdata 的默认处理
* XMLHttpRequest会对 formdata 进行正确的处理
*/
processData: false ,
success: function (data) {

},
error: function () { alert("请关闭execl按正确流程操作！！！"); }
})
})

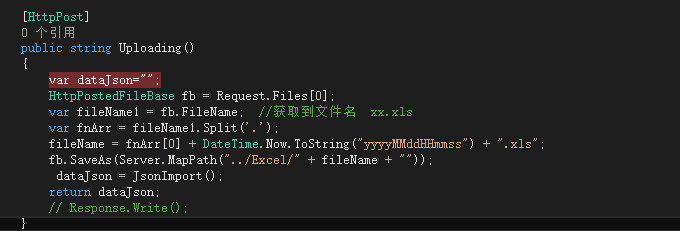
[HttpPost]
public string JsonImport() ////////////////////////////EXECL导入datable
{
string path = string.Concat(System.AppDomain.CurrentDomain.BaseDirectory, "Excel\\" + fileName + ""); //获取项目物理路径
var json = "";
// HSSFWorkbookhssfworkbook;
#region//初始化信息
try
{
using (FileStream file = new FileStream(path, FileMode.Open, FileAccess.Read))
{
IWorkbook wk;
if (path.Equals(".xls"))
{
wk = new XSSFWorkbook(file);

}
else
{
wk = new HSSFWorkbook(file);
}

ISheet sheet = wk.GetSheetAt(0);
DataTable table = new DataTable();
IRow headerRow = sheet.GetRow(0);//第一行为标题行
int cellCount = headerRow.LastCellNum;//LastCellNum =PhysicalNumberOfCells
int rowCount = sheet.LastRowNum;//LastRowNum = PhysicalNumberOfRows - 1
//handling header.
for (int i = headerRow.FirstCellNum; i < cellCount; i++)
{
DataColumn column = new DataColumn(headerRow.GetCell(i).StringCellValue);
table.Columns.Add(column);
}
for (int i = (sheet.FirstRowNum + 1); i <= rowCount; i++)
{
IRow row = sheet.GetRow(i);
DataRow dataRow = table.NewRow();
if (row != null)
{
for (int j = row.FirstCellNum; j < cellCount; j++)
{
if (row.GetCell(j) != null)
dataRow[j] = GetCellValue(row.GetCell(j));
}
}
table.Rows.Add(dataRow);
}
json = JsonConvert.SerializeObject(table);
}

}
catch (Exception e)
{
throw e;
}
#endregion

return json;

}

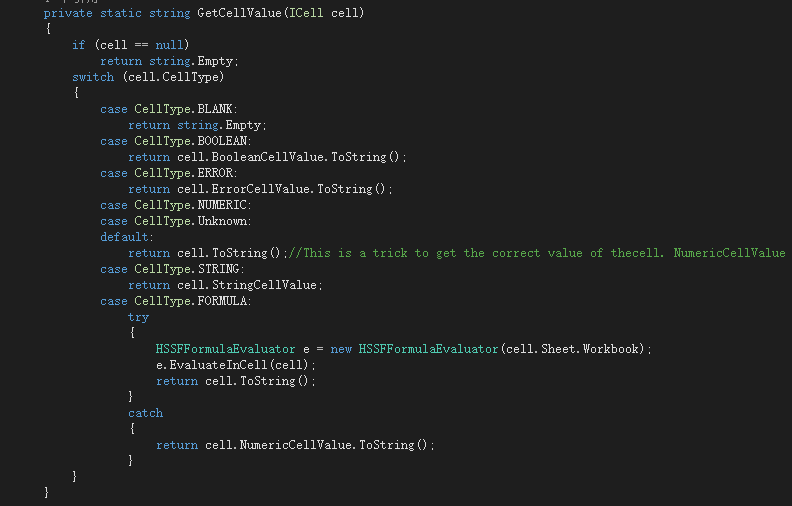
引用文件