UIBezierPath的使用(持续更新)

UIBezierPath的使用

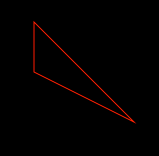
1. 使用UIBezierPath绘制多边形

    // 获取path
    UIBezierPath *aPath = [UIBezierPath bezierPath];

    // 设定起始点
    [aPath moveToPoint:CGPointMake(0.0f, 0.0f)];

    // 添加点
    [aPath addLineToPoint:CGPointMake(100.0f, 100.0f)];
    [aPath addLineToPoint:CGPointMake(.f, .f)];

    // 闭合path
    [aPath closePath];

2. 使用UIBezierPath绘制圆形

    // 将常数转换为度数
    #define   DEGREES(degrees)  ((3.14159265359f * degrees)/ 180.f)

    // 获取path
    UIBezierPath *aPath = \
    [UIBezierPath bezierPathWithArcCenter:CGPointMake(, ) // 圆的中心
                                   radius:.f                // 圆的半径
                               startAngle:DEGREES()          // 起始点
                                 endAngle:DEGREES()        // 结束点
                                clockwise:YES];               // 顺时针

3. 使用UIBezierPath绘制矩形

    // 获取path
    UIBezierPath *aPath = [UIBezierPath bezierPathWithRect:CGRectMake(, , , )];

4. 使用UIBezierPath绘制椭圆

    // 获取path
    UIBezierPath *aPath = [UIBezierPath bezierPathWithOvalInRect:CGRectMake(, , , )];

5. 使用UIBezierPath绘制圆角矩形

    // 获取path
    UIBezierPath *aPath = [UIBezierPath bezierPathWithRoundedRect:CGRectMake(, , , )
                                                     cornerRadius:.f];

6. 使用UIBezierPath绘制带部分圆角的矩形

    // 获取path
    UIBezierPath *aPath = [UIBezierPath bezierPathWithRoundedRect:CGRectMake(, , , )
                                                byRoundingCorners:UIRectCornerTopLeft
                                                      cornerRadii:CGSizeMake(, )];

7. 使用UIBezierPath绘制不规则曲线1

    // 获取path
    UIBezierPath *aPath = [UIBezierPath bezierPath];
    
    // 设定起始点
    [aPath moveToPoint:CGPointMake(0.0f, 0.0f)];
    
    // 添加一个不规则点
    [aPath addCurveToPoint:CGPointMake(100.f, 100.f)
             controlPoint1:CGPointMake(50.f, 0.f)     // 开始点
             controlPoint2:CGPointMake(0.f, 50.f)];   // 结束点
    
    // 添加一个点
    [aPath addLineToPoint:CGPointMake(0.0f, 100.f)];
    
    // 闭合path
    [aPath closePath];

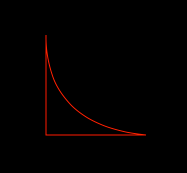
8. 使用UIBezierPath绘制不规则曲线2

    // 获取path
    UIBezierPath *aPath = [UIBezierPath bezierPath];

    // 设定起始点
    [aPath moveToPoint:CGPointMake(0.0f, 0.0f)];

    // 添加一个不规则点
    [aPath addQuadCurveToPoint:CGPointMake(.f, .f)
                  controlPoint:CGPointMake(.f, .f)];   // 控制点

    // 添加一个点
    [aPath addLineToPoint:CGPointMake(0.0f, .f)];

    // 闭合path
    [aPath closePath];

9. 使用path与CAShapeLayer配合制作mask遮罩效果(path闭环里面的填充区域就是作为遮罩使用的)

    // 创建一个view
    UIView *showView = [[UIView alloc] initWithFrame:CGRectMake(, , , )];
    showView.backgroundColor = [UIColor greenColor];
    showView.layer.contents = (__bridge id)([UIImage imageNamed:@""].CGImage);

    // 创建一个椭圆的path
    UIBezierPath *aPath = [UIBezierPath bezierPathWithOvalInRect:CGRectMake(, , , )];

    // 创建一个CAShapeLayer并获取椭圆的path
    CAShapeLayer *layer = [CAShapeLayer layer];
    layer.path = aPath.CGPath;

    // 把这个CAShapeLayer添加为mask
    showView.layer.mask = layer;

10. 使用Core Graphics函数去修改path

    UIBezierPath类只是CGPathRef数据类型和path绘图属性的一个封装。虽然通常我 们可以用UIBezierPath类的方法去添加直线段和曲线段，UIBezierPath类还提供了一个属性CGPath，我们可以用来直接修改底层的 path data type。如果我们希望用Core Graphics 框架函数去创建path，则我们要用到此属性。

    有两种方法可以用来修改和UIBezierPath对象相关的path。可以完全的使用Core Graphics函数去修改path，也可以使用Core Graphics函数和UIBezierPath函数混合去修改。第一种方法在某些方面相对来说比较容易。我们可以创建一个CGPathRef数据类型， 并调用我们需要修改path信息的函数。

下面的代码就是赋值一个新的CGPathRef给UIBezierPath对象。

如 果我们使用Core Graphics函数和UIBezierPath函数混合方法，我们必须小心的移动path 信息在两者之间。因为UIBezierPath类拥有自己底层的CGPathRef data type，我们不能简单的检索该类型并直接的修改它。相反，我们应该生成一个副本，然后修改此副本，然后赋值此副本给CGPath属性，如下代码：

Mixing Core Graphics and UIBezierPath calls