VK Cup 2015 - Round 1 E. Rooks and Rectangles 线段树 定点修改，区间最小值

E. Rooks and Rectangles

Time Limit: 1 Sec  Memory Limit: 256 MB

题目连接

http://codeforces.com/problemset/problem/524/E

Description

Polycarpus has a chessboard of size n × m, where k rooks are placed. Polycarpus hasn't yet invented the rules of the game he will play. However, he has already allocated q rectangular areas of special strategic importance on the board, they must be protected well. According to Polycarpus, a rectangular area of ​​the board is well protected if all its vacant squares can be beaten by the rooks that stand on this area. The rooks on the rest of the board do not affect the area's defense. The position of the rooks is fixed and cannot be changed. We remind you that the the rook beats the squares located on the same vertical or horizontal line with it, if there are no other pieces between the square and the rook. Help Polycarpus determine whether all strategically important areas are protected.

Input

The first line contains four integers n, m, k and q (1 ≤ n, m ≤ 100 000, 1 ≤ k, q ≤ 200 000) — the sizes of the board, the number of rooks and the number of strategically important sites. We will consider that the cells of the board are numbered by integers from 1 to n horizontally and from 1 to m vertically. Next k lines contain pairs of integers "x y", describing the positions of the rooks (1 ≤ x ≤ n, 1 ≤ y ≤ m). It is guaranteed that all the rooks are in distinct squares. Next q lines describe the strategically important areas as groups of four integers "x₁ y₁ x₂ y₂" (1 ≤ x₁ ≤ x₂ ≤ n, 1 ≤ y₁ ≤ y₂ ≤ m). The corresponding rectangle area consists of cells (x, y), for which x₁ ≤ x ≤ x₂, y₁ ≤ y ≤ y₂. Strategically important areas can intersect of coincide.

Output

Print q lines. For each strategically important site print "YES" if it is well defended and "NO" otherwise.

Sample Input

4 3 3 3
1 1
3 2
2 3
2 3 2 3
2 1 3 3
1 2 2 3

Sample Output

YES
YES
NO

HINT

Picture to the sample: 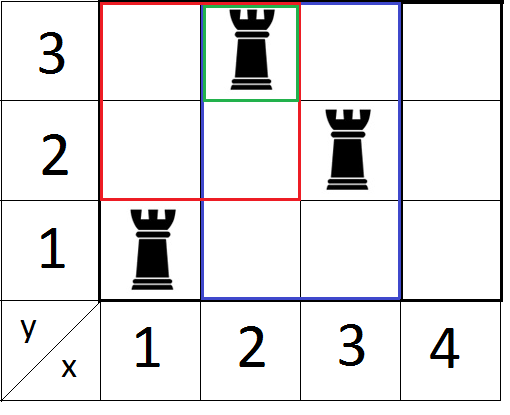For the last area the answer is "NO", because cell (1, 2) cannot be hit by a rook.

题意

给你，n个矩形，判断这个n个矩形是否被在矩形内的车全部覆盖

题解：

维护两个数据结构分别表示前i行里第几列是否被覆盖到和前i列里第j行是否被覆盖到

 

然后询问的时候就相当于查询第i1到第i2行这个区间的线段树中第j1到第j2列中最小的覆盖数是否为0，如果是就说明未被覆盖

思想比较麻烦，但是写起来特别快

 

代码：

//qscqesze
#include <cstdio>
#include <cmath>
#include <cstring>
#include <ctime>
#include <iostream>
#include <algorithm>
#include <set>
#include <vector>
#include <sstream>
#include <queue>
#include <typeinfo>
#include <fstream>
#include <map>
typedef long long ll;
using namespace std;
//freopen("D.in","r",stdin);
//freopen("D.out","w",stdout);
#define sspeed ios_base::sync_with_stdio(0);cin.tie(0)
#define maxn 500001
#define mod 10007
#define eps 1e-9
//const int inf=0x7fffffff;   //无限大
const int inf=0x3f3f3f3f;
/*
inline ll read()
{
    int x=0,f=1;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
int buf[10];
inline void write(int i) {
  int p = 0;if(i == 0) p++;
  else while(i) {buf[p++] = i % 10;i /= 10;}
  for(int j = p-1; j >=0; j--) putchar('0' + buf[j]);
  printf("\n");
}
*/
//**************************************************************************************
int a[maxn],n,m,k,q;;
struct node
{
    int x,y;
};
node p[maxn];
struct pp
{
    int x1,y1,x2,y2,id;
};
pp que[maxn];

void updata(int xx, int L, int R, int x, int val)
{
    if(L==R)
    {
        a[xx]=val;
        return;
    }
    int M=(L+R)>>;
    if(x <= M)
        updata(xx*,L,M,x,val);
    else
        updata(xx*+,M+,R,x,val);
    a[xx]=min(a[xx*], a[xx*+]);
}
int query(int x, int L, int R, int l, int r)
{
    if(l<=L&&R<=r)
        return a[x];
    int M=(L+R)>>;
    if(r<=M)
        return query(x*,L,M,l,r);
    else if(l>M)
        return query(x*+,M+,R,l,r);
    else
        return min(query(x*,L,M,l,r), query(x*+,M+,R,l,r));
}
bool cmp(node x,node y)
{
    return x.x<y.x;
}
bool cmp1(pp x,pp y)
{
    return x.x2<y.x2;
}
int ans[maxn];
void solve()
{
    memset(a,,sizeof(a));
    int pic=;
    for(int i=;i<q;i++)
    {
        while(pic<k&&p[pic].x<=que[i].x2)
        {
            updata(,,m,p[pic].y,p[pic].x);
            pic++;
        }
        if(query(,,m,que[i].y1,que[i].y2)>=que[i].x1)
            ans[que[i].id]=;
    }
}
void change()
{
    swap(n,m);
    for(int i=;i<k;i++)
        swap(p[i].x,p[i].y);
    sort(p,p+k,cmp);
    for(int i=;i<q;i++)
    {
        swap(que[i].x1,que[i].y1);
        swap(que[i].x2,que[i].y2);
    }
    sort(que,que+q,cmp1);
}
int main()
{

    scanf("%d%d%d%d",&n,&m,&k,&q);
    for(int i=;i<k;i++)
        scanf("%d%d",&p[i].x,&p[i].y);
    sort(p,p+k,cmp);
    for(int i=;i<q;i++)
    {
        scanf("%d%d%d%d",&que[i].x1,&que[i].y1,&que[i].x2,&que[i].y2);
        que[i].id=i;
    }
    sort(que,que+q,cmp1);
    solve();
    change();
    solve();
    for(int i=;i<q;i++)
    {
        if(ans[i])
            puts("YES");
        else
            puts("NO");
    }
}