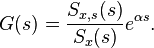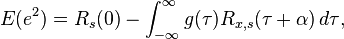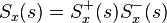基于winner 滤波平稳降噪效果
https://en.wikipedia.org/wiki/Wiener_filter
Wiener filter solutions
The Wiener filter problem has solutions for three possible cases: one where a noncausal filter is acceptable (requiring an infinite amount of both past and future data), the case where a causal filter is desired (using an infinite amount of past data), and the finite impulse response (FIR) case where a finite amount of past data is used. The first c
ase is simple to solve but is not suited for real-time applications. Wiener's main accomplishment was solving the case where the causality requirement is in effect, and in an appendix of Wiener's book Levinson gave the FIR solution.
Noncausal solution
Where  are spectra. Provided that
are spectra. Provided that  is optimal, then the minimum mean-square error equation reduces to
is optimal, then the minimum mean-square error equation reduces to
and the solution  is the inverse two-sided Laplace transform of
is the inverse two-sided Laplace transform of  .
.
Causal solution
where
 consists of the causal part of
consists of the causal part of 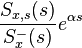 (that is, that part of this fraction having a positive time solution under the inverse Laplace transform)
(that is, that part of this fraction having a positive time solution under the inverse Laplace transform)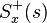 is the causal component of
is the causal component of 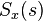 (i.e., the inverse Laplace transform of
(i.e., the inverse Laplace transform of 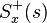 is non-zero only for
is non-zero only for  )
)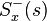 is the anti-causal component of
is the anti-causal component of 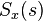 (i.e., the inverse Laplace transform of
(i.e., the inverse Laplace transform of 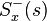 is non-zero only for
is non-zero only for 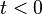 )
)
This general formula is complicated and deserves a more detailed explanation. To write down the solution  in a specific case, one should follow these steps:[2]
in a specific case, one should follow these steps:[2]
- Start with the spectrum
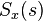 in rational form and factor it into causal and anti-causal components:
in rational form and factor it into causal and anti-causal components:
where
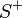 contains all the zeros and poles in the left half plane (LHP) and
contains all the zeros and poles in the left half plane (LHP) and  contains the zeroes and poles in the right half plane (RHP). This is called the Wiener–Hopf factorization.
contains the zeroes and poles in the right half plane (RHP). This is called the Wiener–Hopf factorization. - Divide
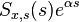 by
by 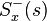 and write out the result as a partial fraction expansion.
and write out the result as a partial fraction expansion. - Select only those terms in this expansion having poles in the LHP. Call these terms
 .
. - Divide
 by
by 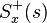 . The result is the desired filter transfer function
. The result is the desired filter transfer function  .
.
原始文件,环境噪音已经很弱了

逐帧实时维纳滤波后

基于winner 滤波平稳降噪效果的更多相关文章
- 基于粒子滤波的物体跟踪 Particle Filter Object Tracking
Video来源地址 一直都觉得粒子滤波是个挺牛的东西,每次试图看文献都被复杂的数学符号搞得看不下去.一个偶然的机会发现了Rob Hess(http://web.engr.oregonstate.edu ...
- 基于GPUImage的实时美颜滤镜
1.背景 前段时间由于项目需求,做了一个基于GPUImage的实时美颜滤镜.现在各种各样的直播.视频App层出不穷,美颜滤镜的需求也越来越多.为了回馈开源,现在我把它放到了GitHub https:/ ...
- 【目标跟踪】相关滤波算法之MOSSE
简要 2010年David S. Bolme等人在CVPR上发表了<Visual Object Tracking using Adaptive Correlation Filters>一文 ...
- 目标跟踪之粒子滤波---Opencv实现粒子滤波算法
目标跟踪学习笔记_2(particle filter初探1) 目标跟踪学习笔记_3(particle filter初探2) 前面2篇博客已经提到当粒子数增加时会内存报错,后面又仔细查了下程序,是代码方 ...
- Canny边缘检测算法(基于OpenCV的Java实现)
目录 Canny边缘检测算法(基于OpenCV的Java实现) 绪论 Canny边缘检测算法的发展历史 Canny边缘检测算法的处理流程 用高斯滤波器平滑图像 彩色RGB图像转换为灰度图像 一维,二维 ...
- Analysis of Two-Channel Generalized Sidelobe Canceller (GSC) With Post-Filtering
作者:凌逆战 地址:https://www.cnblogs.com/LXP-Never/p/12071748.html 题目:带后置滤波的双通道广义旁瓣相消器(GSC)的分析 作者:Israel Co ...
- 论文阅读:Siam-RPN
摘要 Siam-RPN提出了一种基于RPN的孪生网络结构.由孪生子网络和RPN网络组成,它抛弃了传统的多尺度测试和在线跟踪,从而使得跟踪速度非常快.在VOT实时跟踪挑战上达到了最好的效果,速度最高16 ...
- 声学回声消除(Acoustic Echo Cancellation)
回声就是声音信号经过一系列反射之后,又听到了自己讲话的声音,这就是回声.一些回声是必要的,比如剧院里的音乐回声以及延迟时间较短的房间回声:而大多数回声会造成负面影响,比如在有线或者无线通信时重复听到自 ...
- Kernel methods on spike train space for neuroscience: a tutorial
郑重声明:原文参见标题,如有侵权,请联系作者,将会撤销发布! 时序点过程:http://www.tensorinfinity.com/paper_154.html Abstract 在过去的十年中,人 ...
随机推荐
- ACE admin 后台管理框架
一.样式 1.常见按钮 .btn-app .btn-group .btn-corner .btn-xs .btn-sm .btn-mini .btn-minier .btn-defalut .btn ...
- 微信小程序之登录态维护(十一)
[未经作者本人同意,请勿以任何形式转载] >什么是登录态? 所谓登录态,就是程序在运行时,能够识别当前用户,能够证明自己的唯一性且合法. 我们知道,WEB服务器通过浏览器携带的cookie获取s ...
- c语言之【#ifdef】
电脑程序语句,我们可以用它区隔一些与特定头文件.程序库和其他文件版本有关的代码. 1 2 3 #ifdef 语句1 // 程序2 #endif 可翻译为:如果宏定义了语句1则程序2. 作用:我 ...
- 51Nod-1091 线段的重叠
51Nod 1091: http://www.51nod.com/onlineJudge/questionCode.html#!problemId=1091 1091 线段的重叠 基准时间限制: ...
- HtmlUnit初探
HtmlUnit是一个用java实现的浏览器,是一个无界面的浏览器(headless browser),跟phatomJS好像是同一类事物. HtmlUnit基于apache httpClient,而 ...
- Android四大组件之—— 使用服务进行后台操作
什么是服务 服务是一个没有可视化界面的组件,它可以在后台长期运行并进行各种操作. 服务的创建 我们只需要继承Service类并实现相应的方法即可创建服务 要想启动服务,还得在AndroidManife ...
- 1122Shell脚本之利用mysqldump备份MySQL数据库
#!/bin/bash #Mysql 自动备份 压缩并上传到 指定ftp #设想每天凌晨3点备份mysql #编辑crontab配置文件 #00 03 * * * backupmysql.sh #压缩 ...
- Git 本地项目上传至托管平台(OsChina/GitHub)
为了方便自己的代码管理,通常是把自己的写的一些小项目分享到GitHub 或者git.oschina上面! 区别: GitHub 只能创建公开的项目,国外的,速度慢! git.oschina 开源中国的 ...
- MacTalk阅读有感
MacTalk by 池建强 高手的思维境界 -贴地气 -有思想 技术普及 文字是表达人思想的载体,池老师将自己的经历,经验分享给大家,很值得大家学习,虽然我只是个初出茅庐的小菜,现在有指路明灯一样. ...
- BZOJ3505 [Cqoi2014]数三角形
本文版权归ljh2000和博客园共有,欢迎转载,但须保留此声明,并给出原文链接,谢谢合作. 本文作者:ljh2000作者博客:http://www.cnblogs.com/ljh2000-jump/转 ...