freeRTOS学习8-21


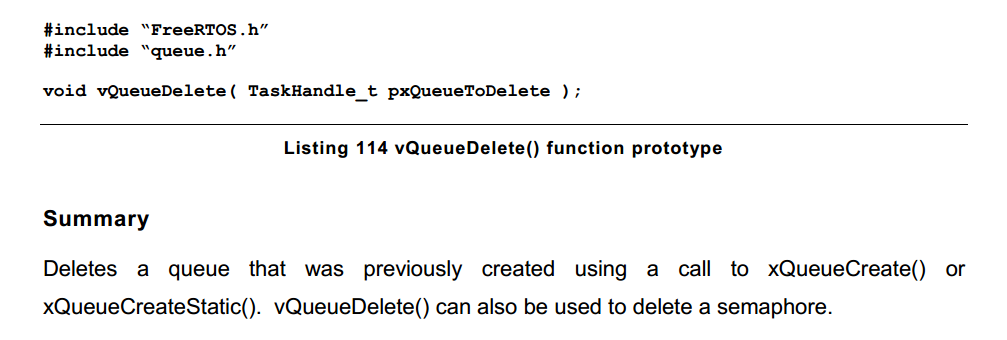

不能再中断服务程序调用该函数 应该调用xQueueSendFromISR()

freeRTOS学习8-21的更多相关文章
- Ext.Net学习笔记21:Ext.Net FormPanel 字段验证(validation)
Ext.Net学习笔记21:Ext.Net FormPanel 字段验证(validation) 作为表单,字段验证当然是不能少的,今天我们来一起看看Ext.Net FormPanel的字段验证功能. ...
- SQL反模式学习笔记21 SQL注入
目标:编写SQL动态查询,防止SQL注入 通常所说的“SQL动态查询”是指将程序中的变量和基本SQL语句拼接成一个完整的查询语句. 反模式:将未经验证的输入作为代码执行 当向SQL查询的字符串中插入别 ...
- 【FreeRTOS学习05】深度解剖FreeRTOSConfig.h实现对系统的自定义剪裁
ROM/RAM太小,因此要对系统进行剪裁: 相关文章 [FreeRTOS实战汇总]小白博主的RTOS学习实战快速进阶之路(持续更新) 文章目录 相关文章 1 系统的剪裁 2 FreeRTOSConfi ...
- FREERTOS学习笔记
2012-02-25 21:43:40 为提升自己对实时操作系统(RTOS)的认识,我学习了freeRTOS. 理解了OS任务的状态.优先级的概念.信号量的概念.互斥的概念.队列.内存管理.这都是和R ...
- FreeRTOS学习及移植笔记之一:开始FreeRTOS之旅
1.必要的准备工作 工欲善其事,必先利其器,在开始学习和移植之前,相应的准备工作必不可少.所以在开始我们写要准备如下: 测试环境:我准备在STM32F103平台上移植和测试FreeRTOS系统 准备F ...
- FreeRTOS学习笔记——任务间使用队列同步数据
1.前言 在嵌入式操作系统中队列是任务间数据交换的常用手段,队列是生产者消费者模型的重要组成部分.FreeRTOS的队列简单易用,下面结合一个具体例子说明FreeRTOS中的队列如何使用. 2.参考代 ...
- SSM(spring mvc+spring+mybatis)学习路径——2-1、spring MVC入门
目录 2-1 Spring MVC起步 一.回顾Servlet 二.SpringMVC简介 三.搭建SpringMVC第一个案例 四.简单流程及配置 五.使用注解开发Controller 六.参数绑定 ...
- Java 学习(21):Java 实例
Java 实例 本章节我们将为大家介绍 Java 常用的实例,通过实例学习我们可以更快的掌握 Java 的应用. Java 环境设置实例 //HelloWorld.java 文件 public cla ...
- 020 - FreeRTOS学习路线总结
零.为什么写? 在H7-tools预售群里,有位朋友提出如何学习FreeRTOS这类的问题,便由此总结下自己的学习路线.最近又打算接触RTT,和FreeRTOS做个对比. 文章分两步来讲,学习路线和学 ...
- 【FreeRTOS学习06】深度解剖中断与任务之间同步的具体使用场景
嵌入式系统中中断是必不可少的一部分: [FreeRTOS实战汇总]小白博主的RTOS学习实战快速进阶之路(持续更新) 文章目录 1 前言 2 中断特点 3 延迟中断处理 3.1 信号量的使用 3.2 ...
随机推荐
- spring的finishBeanFactoryInitialization方法分析
spring源码版本5.0.5 概述 该方法会实例化所有剩余的非懒加载单例 bean.除了一些内部的 bean.实现了 BeanFactoryPostProcessor 接口的 bean.实现了 Be ...
- 【方法】如何实现图片压缩并使用FormData上传
在前端上传图片的操作过程中,当上传服务器时,如果图片过大,可能会影响页面响应速度,这个时候,我们便会对图片进行压缩处理,再上传服务器. 前端对图片进行压缩,一般使用canvas来实现.最后使用canv ...
- Python基础--基于ubuntu linux基础知识点
part1:Python编译 1.直接在终端编译-----在ubuntu中Python是在home文件夹下的,输入Python(Python2编译,想要Python3直接输入python3) 一般推荐 ...
- 快速弄清JavaScript中undefined和null的区别
ES6的7大数据类型里面有这俩玩意:undefined和null,让接触不深的学习者常常产生混淆,这俩玩意的区别在哪呢? 字面意思上来看,undefined是未(被我们)阐明的,未说明的,null则意 ...
- const 与指针 的用法
请找出下面程序中有哪些错误: 1 2 3 4 5 6 7 8 9 10 11 12 13 int main() { int i=10; int j=1; const int *p1; ...
- 在Idea中 的terminal 使用 git
参考该博客内容 http://blog.csdn.net/qq_28867949/article/details/73012300
- ACM之路(13)—— 树型dp
最近刷了一套(5题)的树型dp题目:http://acm.hust.edu.cn/vjudge/contest/view.action?cid=116767#overview,算是入了个门,做下总结. ...
- $\LaTeX$数学公式大全
$\LaTeX$数学公式大全$1\ Geek\ and\ Hebrew\ letters$ $\LaTeX$数学公式大全$2\ Math\ Constructs$ $\LaTeX$数学公式大全$3\ ...
- deep sort
目录 1. 准备代码与数据 deep_sort开源代码 克隆到本地服务器 git clone https://github.com/nwojke/deep_sort.git 下载MOT16数据集( ...
- 2018-2019-2 20165330《网络对抗技术》Exp8 Web基础
目录 基础问题 相关知识 实验内容 实验步骤 实验总结与体会 实验内容 Web前端HTML 能正常安装.启停Apache.理解HTML,理解表单,理解GET与POST方法,编写一个含有表单的HTML ...
