非监督的降维算法--PCA

PCA是一种非监督学习算法，它能够在保留大多数有用信息的情况下，有效降低数据纬度。

它主要应用在以下三个方面：

1. 提升算法速度

2. 压缩数据，减小内存、硬盘空间的消耗

3. 图示化数据，将高纬数据映射到2维或3维

总而言之，PCA干的事情就是完成一个将原始的n维数据转化到k维的映射。其中，k<n

它的核心算法如下：

1. 将数据均一化

x' = [x-mean(x)] / range(x)

2. 计算它的协方差矩阵

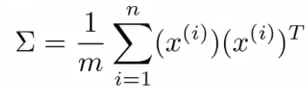
即：Sigma = 1/m * x' * x

3. 进行svd分解，计算特征向量

[U, S, V] = svd(Sigma)

选出U中的前k列，就可以得到映射公式啦

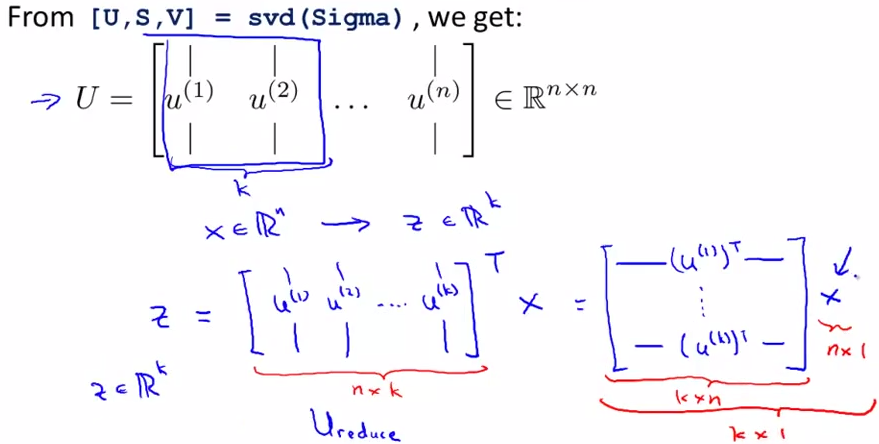
即：

Ureduce = U(:, 1:k);

z = Ureduce'*x;

其中，z便是降维后映射得到的特征矩阵。

至于如何选择k，那要看我们决定保留原始信息的多少变化范围（variance）。当我们想保留

原始信息99%的variance时：

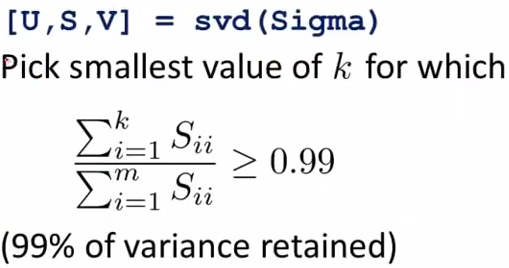
即：将S中前k个对角线元素相加，最小的能使相加和大于整个S的对角线和的99%的k便是我们应选择的k。

有压缩，那自然就有相应的还原。不过PCA本身的压缩是有损压缩，无法还原为与原来完全一样的值。（当然k=n另当别论）

我们只能够得到原始特征向量（非矩阵）的近似还原值。公式为：

即：Xapprox = Ureduce * Z

在使用PCA时，有几个要注意的地方：

1. 构建机器学习算法时，不要一上来就想要用PCA，一般而言，直接使用原始特征效果会比较好。

PCA是在原始算法过于缓慢，或者内存、硬盘空间实在不够大无法支撑计算时才有必要加入的

2. 不要用PCA来减小过拟合的问题，用regularization才是解决过拟合更为合理的方法。因为

PCA只看特征矩阵来决定如何减小特征数，而regularization同时看特征矩阵和对应的label来减小过拟合。