第一次作业-----四则运算题目生成（基于java）

1.题目要求

1.除了整数以外，还要支持真分数的四则运算，真分数的运算，例如：1/6 + 1/8 = 7/24。
2.运算符为 +, −, ×, ÷。
3.并且要求能处理用户的输入，并判断对错，打分统计正确率。
4.要求能处理用户输入的真分数， 如 1/2, 5/12 等。
5.使用 -n 参数控制生成题目的个数，例如执行下面命令将生成10个题目Myapp.exe -n 10。

2.功能分析

• 能随机生成包括+, −, ×, ÷的两个数直接的运算。
• 能够从命令行读取输入的答案进行匹配，并判断对错。
• 能够统计答题数量与正确率。
• 能够自己根据需求生成题目个数与数值范围。

3.程序设计

• 首先要有一个分子类 Fraction，类中包含分子 Numerator，分母 Denominator，与一个用来表示分数形式的字符串 fraction。

  public class Fraction {
      private int Numerator;
      private int Denominator;
      private String fraction;
  }

• 同时在分子类中还有一个生成随机分数的方法，m表示数值的范围。

  public String creatfraction(int m) //创建分数并且化为最简
  	{
  		int i, j;
  		Numerator = (int) (Math.random() * m + 1);
  		Denominator = (int) (Math.random() * m + 1);
  		i = Numerator;
  		j = Denominator;
  		j = Mathod.getGCD(i, j);
  		Numerator = Numerator / j;
  		Denominator = Denominator / j;
  		fraction = Mathod.Reduction(Numerator, Denominator);
  		return fraction;
  	}

• 对于加、减、乘、除计算在一个计算类 Calculate 中写四个对应的函数，在每个方法中传入两个分子类对象。

public class Calculate {
	public String add(Fraction a, Fraction b) //加法 参考分数间加减乘除 用四个变量表示两个分数的分子分母
	{
		int i, j, k, s, m, n, p;
		i = a.getNumerator();// 分子
		j = a.getDenominator();// 分母
		k = b.getNumerator();
		s = b.getDenominator();
		m = i * s + j * k;
		n = s * j;
		p = Mathod.getGCD(m, n);
		return Mathod.Reduction(m / p, n / p);
	}
	public String div(Fraction a, Fraction b)//除法  设置生成的随机数不为0，则不存在除数为0的情况
	{
		int i, j, k, s, m, n, p;
		i = a.getNumerator();// 分子
		j = a.getDenominator();// 分母
		k = b.getNumerator();
		s = b.getDenominator();
		m = s * i;
		n = j * k;
		p = Mathod.getGCD(m, n);
		return Mathod.Reduction(m / p, n / p);
	}
	public String sub(Fraction a, Fraction b)//减法
	{
		int i, j, k, s, m, n, p;
		i = a.getNumerator();// 分子
		j = a.getDenominator();// 分母
		k = b.getNumerator();
		s = b.getDenominator();
		m = i * s - j * k; //会产生负数，当当负号表示时可能出现不规范例如9/-8，负号在后。
		n = j * s;
		p = Mathod.getGCD(m, n);
		return Mathod.Reduction(m / p, n / p);
	}
	public String mul(Fraction a, Fraction b)//乘法
	{
		int i, j, k, s, m, n, p;
		i = a.getNumerator();// 分子
		j = a.getDenominator();// 分母
		k = b.getNumerator();
		s = b.getDenominator();
		m = i * k;
		n = j * s;
		p = Mathod.getGCD(m, n);
		return Mathod.Reduction(m / p, n / p);
	}
}

• 在构造分数和最后统计对错时会使用到一些方法所以有一个方法类，例如求最大公约数 getGCD 、约分 Reduction、比较答案等 compare。

static int getGCD(int i, int j) //求最大公约数 辗转相除法。
	{
		int temp;
		while (i % j != 0) {
			temp = i % j;
			i = j;
			j = temp;
		}
		return j;
	}

static String Reduction(int i, int j) //约分，化为最简。
	{
		String k;
		if (j == 1) {
			k = i + "";
		} else {
			k = (i) + "" + "/" + (j) + "";
		}
		return k;
	}

static boolean compare(String a, String b) //比较输入值与答案，返回值为boolean类型。
	{
		if (a.equals(b))
			{System.out.println("回答正确");
		    return true;}
		else
			{
			System.out.println("回答错误，正确答案是" + b);
			return false;
			}
	}

• 在Test类中写main函数执行。

import java.util.Scanner;
public class Test {
	@SuppressWarnings("resource")
	public static void main(String[] args) {
		Fraction f1 = new Fraction();
		Fraction f2 = new Fraction();
		int m;
		int op;
		int right=0,wrong=0;
		Scanner s1 = new Scanner(System.in);
		Calculate c = new Calculate();
		System.out.println("输入题目数");
		int i = s1.nextInt();
		Scanner scanneer = new Scanner(System.in);
		String s2;
		Scanner s3 = new Scanner(System.in);
		System.out.println("输入范围");
		m = s3.nextInt();
		for (int j = 0; j < i; j++) {
			f1.creatfraction(m);
			f2.creatfraction(m);
			op = (int) (Math.random() * 4 + 1);
			switch (op) {
			case 1: {
				System.out.println(f1.getFraction() + " " + "+" + " " + f2.getFraction() + " =");
				s2 = c.add(f1, f2);
				String intput = scanneer.nextLine();
				if(Mathod.compare(intput, s2))
					right++;
				else
					wrong++;
				break;
			}
			case 2: {
				System.out.println(f1.getFraction() + " " + "-" + " " + f2.getFraction() + " =");
				s2 = c.sub(f1, f2);
				String intput = scanneer.nextLine();
				if(Mathod.compare(intput, s2))
					right++;
				else
					wrong++;
				break;
			}
			case 3: {
				System.out.println(f1.getFraction() + " " + "×" + " " + f2.getFraction() + " =");
				s2 = c.mul(f1, f2);
				String intput = scanneer.nextLine();
				if(Mathod.compare(intput, s2))
					right++;
				else
					wrong++;
				break;
			}
			case 4: {
				System.out.println(f1.getFraction() + " " + "÷" + " " + f2.getFraction() + " =");
				s2 = c.div(f1, f2);
				String intput = scanneer.nextLine();
				if(Mathod.compare(intput, s2))
					right++;
				else
					wrong++;
				break;
			}
			}
		}System.out.println("一共"+i+"题"+" "+"做对"+right+"题"+" "+"做错"+wrong+"题");
	}
}

4.程序测试

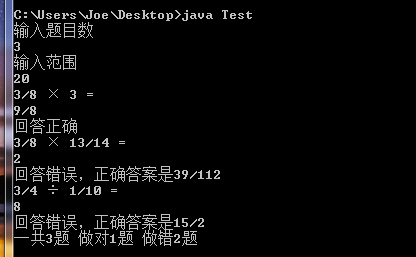
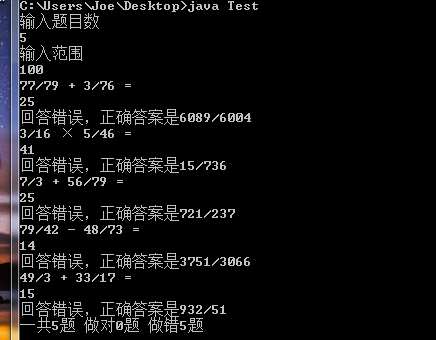
自我评价

总体而言程序有点冗余，其实应该有许多地方都可改变方法达到简化代码，没有经常的动手编程导致许多基础的输入，输出获取数据等都需要在查找书本或资料才能继续。

在设计除法时因为设定生成的数不会为0，所以跳过了除数不为0的判断。许多方法的调用可能也存在一些隐患。

个人水平不足，能力有限，还请大家多多指点。

psp表格

PSP2.1	Personal Software Process Stages	Time (%) Senior Student （hour）	Time (%) （hour）
Planning	计划	12	10
· Estimate	估计这个任务需要多少时间	8	8
Development	开发	4	3
· Analysis	需求分析 (包括学习新技术)	0	0
· Design Spec	生成设计文档	0	0
· Design Review	设计复审	1	1
· Coding Standard	代码规范	0.5	1
· Design	具体设计	10	12
· Coding	具体编码	5	4
Code Review	代码复审	0	0
· Test	测试（自我测试，修改代码，提交修改	3	2
·Reporting	报告	6	3
·	测试报告	0	0
·	计算工作量	0	0
·	并提出过程改进计划	0	0

码市地址

coding.net