面向对象编程 —— java实现函数求导

首先声明一点，本文主要介绍的是面向对象（OO）的思想，顺便谈下函数式编程，而不是教你如何准确地、科学地用java求出函数在一点的导数。

一、引子

def d(f) :
    def calc(x) :
        dx = 0.000001  # 表示无穷小的Δx
        return (f(x+dx) - f(x)) / dx  # 计算斜率。注意，此处引用了外层作用域的变量 f
    return calc  # 此处用函数作为返回值（也就是函数 f 的导数）
# 计算二次函数 f(x) = x2 + x + 1的导数
f = lambda x : x**2 + x + 1  # 先把二次函数用代码表达出来
f1 = d(f)# 这个f1 就是 f 的一阶导数啦。注意，导数依然是个函数
# 计算x=3的斜率
f1(3)
# 二阶导数
f2 = d(f1)

首先，直接上一段python代码，请大家先分析下上面代码是用什么方法求导的。请不要被这段代码吓到，你无需纠结它的语法，只要明白它的求导思路。

以上代码引用自《为啥俺推荐 Python[4]：作为函数式编程语言的 Python》，这篇博客是促使我写篇文章的主要原因。

博主说“如果不用 FP，改用 OOP，上述需求该如何实现？俺觉得吧，用 OOP 来求导，这代码写起来多半是又丑又臭。”

我将信将疑，于是就用面向对象的java试了试，最后也没多少代码。如果用java8或以后版本，代码更少。

请大家思考一个问题，如何用面向对象的思路改写这个程序。请先好好思考，尝试编个程序再继续往下看。

考虑到看到这个标题进来的同学大多是学过java的，下面我用java，用面向对象的思路一步步分析这个问题。

二、求导

文章开头我已近声明过了，本文不是来讨论数学的，求导只是我用来说明面向对象的一个例子。

如果你已经忘了开头那段代码的求导思路，请回头再看看，看看用python是如何求导的。

相信你只要听说过求导，肯定一眼就看出开头那段代码是用导数定义求导的。

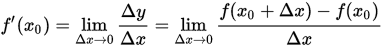
代码中只是将无穷小Δx粗略地算做一个较小的值0.000001。

三、最初的想法

//自定义函数
public class Function {
    //函数：f(x) = 3x^3 + 2x^2 + x + 1
    public double f(double x) {
        return 3 * x * x * x + 2 * x * x + x + 1;
    }
}

//一元函数导函数
public class DerivedFunction {
    //表示无穷小的Δx
    private static final double DELTA_X = 0.000001;
    //待求导的函数
    private Function function;

    public DerivedFunction(Function function) {
        this.function = function;
    }

    /**
     * 获取function在点x处的导数
     * @param x 待求导的点
     * @return 导数
     */
    public double get(double x) {
        return (function.f(x + DELTA_X) - function.f(x)) / DELTA_X;
    }
}

public class Main {
    public static void main(String[] args) {
        //一阶导函数
        DerivedFunction derivative = new DerivedFunction(new Function());
        //打印函数在x=2处的一阶导数
        System.out.println(derivative.get(2));
    }
}

先声明一点，考虑到博客篇幅，我使用了不规范的代码注释，希望大家不要被我误导。

我想只要大家好好思考了，应该至少会想到这步吧。代码我就不解释了，我只是用java改写了文章开头的那段python代码，做了一个简单的翻译工作。再请大家考虑下以上代码的问题。

刚开始，我思考这个问题想到的是建一个名为Function的类，类中有一个名为f的方法。但考虑到要每次要求新的函数导数时就得更改这个f方法的实现，明显不利于扩展，这违背了开闭原则。

估计有的同学没听过这个词，我就解释下：”对象（类，模块，函数等）应对扩展开放，但对修改封闭“。

于是我就没继续写下去，但为了让大家直观的感受到这个想法，我写这篇博客时就实现了一下这个想法。

请大家思考一下如何重构代码以解决扩展性问题。

四、初步的想法

估计学过面向对象的同学会想到把Function类改成接口或抽象类，以后每次添加新的函数时只要重写这个接口或抽象类中的f方法，这就是面向接口编程，符合依赖反转原则，下面的代码就是这么做的。

再声明一点，考虑到篇幅的问题，后面的代码我会省去与之前代码重复的注释，有不明白的地方还请看看上一个想法中的代码。

//一元函数
public interface Function {
    double f(double x);
}

//自定义的函数
public class MyFunction implements Function {
    @Override
    public double f(double x) {
        return 3 * x * x * x + 2 * x * x + x + 1;
    }
}

public class DerivedFunction {
    private static final double DELTA_X = 0.000001;
    private Function function;

    public DerivedFunction(Function function) {
        this.function = function;
    }

    public double get(double x) {
        return (function.f(x + DELTA_X) - function.f(x)) / DELTA_X;
    }
}

public class Main {
    public static void main(String[] args) {
        //一阶导函数：f'(x) = 9x^2 + 4x + 1
        DerivedFunction derivative = new DerivedFunction(new MyFunction());
        System.out.println(derivative.get(2));
    }
}

我想认真看的同学可能会发现一个问题，我的翻译做的还不到位，开头那段python代码还可以轻松地求出二阶导函数（导数的导数），而我的代码却不行。

其实只要稍微修改以上代码的一个地方就可以轻松实现求二阶导，请再思考片刻。

五、后来的想法

当我写出上面的代码时，我感觉完全可以否定“用 OOP 来求导，这代码写起来多半是又丑又臭”的观点。但还不能求二阶导，我有点不甘心。

于是我就动笔，列了一下用定义求一阶导和求二阶导的式子，想了想两个式子的区别与联系，突然想到导函数也是函数。

DerivedFunction的get方法和Function的f方法的参数和返回值一样，DerivedFunction可以实现Function接口，于是产生了下面的代码。

public interface Function {
    double f(double x);
}

public class DerivedFunction implements Function {
    private static final double DELTA_X = 0.000001;
    private Function function;

    public DerivedFunction(Function function) {
        this.function = function;
    }

    @Override
    public double f(double x) {
        return (function.f(x + DELTA_X) - function.f(x)) / DELTA_X;
    }
}

public class Main {
    public static void main(String[] args) {
        Function f1 = new DerivedFunction(new Function() {
            @Override
            public double f(double x) {
                return 3 * x * x * x + 2 * x * x + x + 1;
            }
        });
        System.out.println(f1.f(2));
        //二阶导函数：f''(x) = 18x + 4
        Function f2 = new DerivedFunction(f1);
        //打印函数f(x) = 3x^3 + 2x^2 + x + 1在x=2处的二阶导数
        System.out.println(f2.f(2));
    }
}

考虑到有的同学没学过java8或以上版本，以上代码没有用到java8函数式编程的新特性。

如果你接触过java8，请考虑如何改写以上代码，使其更简洁。

六、最后的想法

public class DerivedFunction implements Function<Double, Double> {
    private static final double DELTA_X = 0.000001;
    private Function<Double, Double> function;

    public DerivedFunction(Function<Double, Double> function) {
        this.function = function;
    }

    @Override
    public Double apply(Double x) {
        return (function.apply(x + DELTA_X) - function.apply(x)) / DELTA_X;
    }
}

public class Main {
    public static void main(String[] args) {
        //打印函数在x=2处的二阶导
        System.out.println(new DerivedFunction(new DerivedFunction(x -> 3 * x * x * x + 2 * x * x + x + 1)).apply(2.0));
    }
}

之前几个想法为了扩展Function接口，使用了外部类、匿名类的方式，其实也可以用内部类。而这在这里，我用了lambda表达式，是不是更简洁了。

这里用的Function接口用的是jdk自带的，我们不需要自己定义了。因为这是一个函数式接口，我们可以用lambda方便地实现。后来发现，其实这里用UnaryOperator这个接口更恰当。

现在大家有没有发现，用java、用OOP也可以非常简洁地实现求导，并不比开头的那段python代码麻烦很多。

七、编程范式

在我看来，编程范式简单来说就是编程的一种模式，一种风格。

我先介绍其中的三个，你差不多就知道它的含义了。

7.1 面向对象程序设计（OOP）

看到这里的同学应该对面向对象有了更直观的认识。在面向对象编程中，万物皆对象，抽象出类的概念。基本特性是封装、继承、多态，认识不深的同学可以再去我之前的代码中找找这三个特性。

我之前还介绍了面向对象的几个原则：开闭原则、依赖反转原则。其他还有单一职责原则、里氏替换原则、接口隔离原则。这是面向对象的5个基本原则，合称SOLID。

7.2 函数编程语言（FP）

本文开头那段代码用的就是python函数式编程的语法，后来我又用java8函数式编程的语法翻译了这段代码。

相信你已经直观地感受到它的简洁，以函数为核心，几行代码就解决了求导的问题。

7.3 过程式编程（Procedural programming）

大概学过编程都学过C，C语言就是一种过程式编程语言。在我看来，过程式编程大概就是为了完成一个需求，像记流水帐一样，平铺直叙下去。

　　

八、结尾

由于本人初学java，目前只能想到这么多。如果大家有更好的想法或者觉的我上面说的有问题，欢迎评论，望各位不吝赐教。

这是我的第一篇技术博客，但愿我说清楚了面向对象。如果对你有帮助，请点个赞或者评论下，给我点继续创作的动力。