机器学习:形如抛物线的散点图在python和R中的非线性回归拟合方法
对于样本数据的散点图形如函数y=ax2+bx+c的图像的数据, 在python中的拟合过程为:
##最小二乘法
import numpy as np
import scipy as sp
import matplotlib.pyplot as plt
from scipy.optimize import leastsq '''
设置样本数据,真实数据需要在这里处理
'''
##样本数据(Xi,Yi),需要转换成数组(列表)形式
Xi=np.array([1,2,3,4,5,6])
#Yi=np.array([9,18,31,48,69,94])
Yi=np.array([9.1,18.3,32,47,69.5,94.8]) '''
设定拟合函数和偏差函数
函数的形状确定过程:
1.先画样本图像
2.根据样本图像大致形状确定函数形式(直线、抛物线、正弦余弦等)
''' ##需要拟合的函数func :指定函数的形状
def func(p,x):
a,b,c=p
return a*x*x+b*x+c ##偏差函数:x,y都是列表:这里的x,y更上面的Xi,Yi中是一一对应的
def error(p,x,y):
return func(p,x)-y '''
主要部分:附带部分说明
1.leastsq函数的返回值tuple,第一个元素是求解结果,第二个是求解的代价值(个人理解)
2.官网的原话(第二个值):Value of the cost function at the solution
3.实例:Para=>(array([ 0.61349535, 1.79409255]), 3)
4.返回值元组中第一个值的数量跟需要求解的参数的数量一致
''' #k,b的初始值,可以任意设定,经过几次试验,发现p0的值会影响cost的值:Para[1]
p0=[10,10,10] #把error函数中除了p0以外的参数打包到args中(使用要求)
Para=leastsq(error,p0,args=(Xi,Yi)) #读取结果
a,b,c=Para[0]
print("a=",a,"b=",b,"c=",c)
print("cost:"+str(Para[1]))
print("求解的拟合直线为:")
print("y="+str(round(a,2))+"x*x+"+str(round(b,2))+"x+"+str(c)) '''
绘图,看拟合效果.
matplotlib默认不支持中文,label设置中文的话需要另行设置
如果报错,改成英文就可以
''' #画样本点
plt.figure(figsize=(8,6)) ##指定图像比例: 8:6
plt.scatter(Xi,Yi,color="green",label="样本数据",linewidth=2) #画拟合直线
x=np.linspace(0,12,100) ##在0-15直接画100个连续点
y=a*x*x+b*x+c ##函数式
plt.plot(x,y,color="red",label="拟合直线",linewidth=2)
plt.legend() #绘制图例
plt.show()
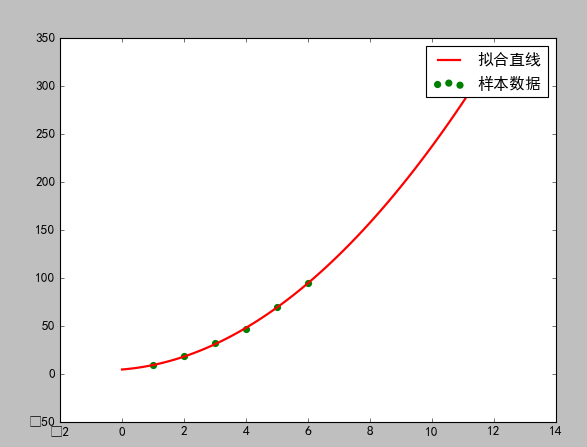
运行结果:
a= 2.06607141425 b= 2.5975001036 c= 4.68999985496
cost:1
求解的拟合直线为:
y=2.07x*x+2.6x+4.68999985496
在R中的拟合过程:(在控制台直接敲入或者放入脚本都可以)
###设置函数形式
func<-function(a,b,c){
a*x*x+b*x+c
}
###设置样本数据
x<-c(1,2,3,4,5,6)
y<-c(9.1,18.3,32,47,69.5,94.8)
###把样本数据转换为符合nls函数需要的格式
d<-data.frame(y,x)
###执行求解过程:如果x,y值完全一一对应,汇报错误(循环次数超过了50这个最大值)
nlmod<-nls(y ~ func(a1,b1,c1),data=d,start=list(a1=1,b1=1,c1=1),trace=F)
###分析结果
summary(nlmod)
运行结果:
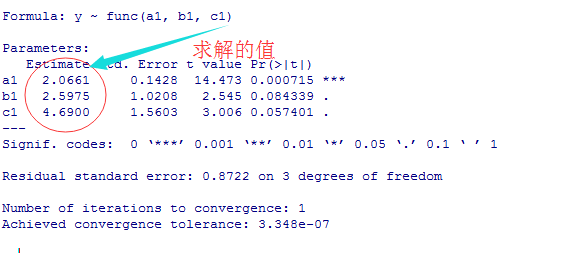
机器学习:形如抛物线的散点图在python和R中的非线性回归拟合方法的更多相关文章
- 机器学习算法的基本知识(使用Python和R代码)
本篇文章是原文的译文,然后自己对其中做了一些修改和添加内容(随机森林和降维算法).文章简洁地介绍了机器学习的主要算法和一些伪代码,对于初学者有很大帮助,是一篇不错的总结文章,后期可以通过文中提到的算法 ...
- (数据科学学习手札22)主成分分析法在Python与R中的基本功能实现
上一篇中我们详细介绍推导了主成分分析法的原理,并基于Python通过自编函数实现了挑选主成分的过程,而在Python与R中都有比较成熟的主成分分析函数,本篇我们就对这些方法进行介绍: R 在R的基础函 ...
- python去除列表中重复元素的方法
列表中元素位置的索引用的是L.index 本文实例讲述了Python去除列表中重复元素的方法.分享给大家供大家参考.具体如下: 比较容易记忆的是用内置的set 1 2 3 l1 = ['b','c', ...
- python 和 R 中的整数序列
python 中的 range() 函数是很常用的,R 中相应的函数是 seq(), 其实,R 中的“ :”也能代替 python 中的 range() 函数. 1.生成升序整数序列 python: ...
- python 获取类中除内置方法外的所有方法名
#!/usr/bin/env python# !-*- coding:utf-8 -*- class Menu: def __init__(self): pass def updateProject( ...
- Python及R安装包版本查看方法
R包查询 查询已安装的所有的包:library() 或installed.packages()(括号内为空,区别以上两项) 查询具体包的信息: help(package="pheatmap& ...
- Python 和 R 中的一数多图
R # 一数多图 x <- 2:6 y <- 7:3 y1 <- y +2 opar <- par(no.readonly = TRUE) par(mfrow=c(2, 3)) ...
- Python向excel中写入数据的方法 方法简单
最近做了一项工作需要把处理的数据写入到Excel表格中进行保存,所以在此就简单介绍使用Python如何把数据保存到excel表格中. 数据导入之前需要安装 xlwt依赖包,安装的方法就很简单,直接 p ...
- python文件写中的f.flush()方法
f = open("input.txt", "w") f.write("aaaaaa") f.flush() #强行把缓冲区中的内容放到磁盘 ...
随机推荐
- 蓝牙门禁Android客户端
先来了解下Android传统蓝牙连接的大致简单的流程: 其中涉及到几个类依次来介绍,废话不多说,下面是从Android4.4开发指南蓝牙所用到的类的截图: 第一个类BluetoothAdapter: ...
- bootstrap_下拉菜单+头部
<!DOCTYPE html> <html lang="en"> <head> <meta charset="UTF-8&quo ...
- ZwQueryVirtualMemory枚举进程模块
ZwQueryVirtualMemory算是枚举进程方法中的黑科技吧,主要是该方法可以检测出隐藏的模块(类似IceSword). 代码VS2015测试通过 再次奉上源码链接:https://githu ...
- MVC和三层架构
从最开始写程序到现在,一路上听到架构这个词已经无数次了,在工作和圈子里也不停听到大家在讨论它,但是很多时候发现不少人对这个概念的理解都是很模糊的,无意间在知道上看到一个朋友的回答,感觉很不错,特转帖到 ...
- [编织消息框架][rpc]使用篇
rpc 分两部份,一个是调用者,另一方是服务提供者 调用者只关心那个服务,传相应参数,返回内容就可以 而提供者根据调用相应服务同参数,工作处理后响应内容即可 根据他们的关系可以用JAVA 接口同实现类 ...
- linux数据库初始化配置
mysql: 第一次登陆mysql -uroot -p,密码输入直接回车,以空密码登陆 选择数据库:use mysql; UPDATE user SET password=PASSWORD('Java ...
- winform调用cmd命令
string str = Console.ReadLine(); System.Diagnostics.Process p = new System.Diagnostics.Process(); p. ...
- 多线程简介及GCD的使用
多线程简介: 对于任意一个iOS应用,程序运行起来后,默认会产生一个主线程(MainThread),主线程专门用来处理UIKit对象的操作,如界面的显示与更新.处理用户事件触发的操作等等.(记忆这点, ...
- redis 扩展下载
自己保存一下 免得以后忘记还得重新找T-T http://windows.php.net/downloads/pecl/snaps/redis/2.2.5/ phpinfo查看自己的php信息下载对 ...
- Linux下修改系统时区
使用 /etc/localtime 文件修改时区 先查看一下当前的时区,下面这个例子中使用 UTC 即世界统一标准时区.假设你可能需要改为美国西部标准时间,即太平洋时间. # date Thu Aug ...
