poj 3321Apple Tree

Apple Tree

Time Limit:2000MS     Memory Limit:65536KB     64bit IO Format:%I64d & %I64u

Submit Status

Description

There is an apple tree outside of kaka's house. Every autumn, a lot of apples will grow in the tree. Kaka likes apple very much, so he has been carefully nurturing the big apple tree.

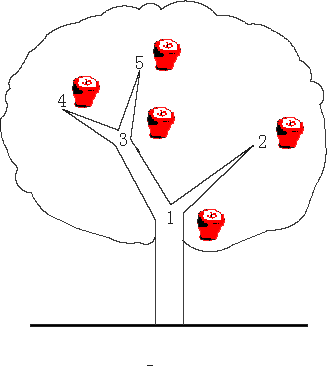
The tree has N forks which are connected by branches. Kaka numbers the forks by 1 to N and the root is always numbered by 1. Apples will grow on the forks and two apple won't grow on the same fork. kaka wants to know how many apples are there in a sub-tree, for his study of the produce ability of the apple tree.

The trouble is that a new apple may grow on an empty fork some time and kaka may pick an apple from the tree for his dessert. Can you help kaka?

Input

The first line contains an integer N (N ≤ 100,000) , which is the number of the forks in the tree.
The following N - 1 lines each contain two integers u and v, which means fork u and fork v are connected by a branch.
The next line contains an integer M (M ≤ 100,000).
The following M lines each contain a message which is either
"C x" which means the existence of the apple on fork x has been changed. i.e. if there is an apple on the fork, then Kaka pick it; otherwise a new apple has grown on the empty fork.
or
"Q x" which means an inquiry for the number of apples in the sub-tree above the fork x, including the apple (if exists) on the fork x
Note the tree is full of apples at the beginning

Output

For every inquiry, output the correspond answer per line.

Sample Input

3
1 2
1 3
3
Q 1
C 2
Q 1

Sample Output

3
2

/*
题意：给你一棵二叉树，root节点是1，初始的时候每个节点都有一个苹果，两种操作：
    C:x,对x节点的苹果数量进行异或
    Q:x,查询以x节点为根节点的子树的苹果的数量

初步思路：实际上就是建图，然后dfs跑一遍，记录下每个节点的左右区间，注意标记的时候将一个节点表示的区间内的点表示成连续的点，
    然后记录一下区间内点的区间长度，然后用树状数组进行区间求和单点更新

#超时：可能是初始化的时候超时
*/
#include <iostream>
#include <stdio.h>
#include <string.h>
#include <vector>
using namespace std;
const int N=;
int n,m;
char str[];
int Count=;//用于表示重新标记的节点
int Start[N];//用于标记节点区间的开始位置
int End[N];//用于标记节点区间的结束位置
int lowbit[N];
int val[N];
int u,v;
int c[N];
typedef vector<int> VCT_INT;
vector<VCT_INT>edge(N/);//用于构建图（树）
void dfs(int x){
    Start[x]=++Count;
    for(int i=;i<edge[x].size();i++){
        dfs(edge[x][i]);
    }
    End[x]=++Count;
}
void add(int x,int val){
    while(x<=Count){
        c[x]+=val;
        x+=lowbit[x];
    }
}
int sum(int x){
    int res=;
    while(x>){
        res+=c[x];
        x-=lowbit[x];
    }
    return res;
}
int main(){
    // freopen("in.txt","r",stdin);
    scanf("%d",&n);
    for(int i=;i<n-;i++){
        scanf("%d%d",&u,&v);
        edge[u].push_back(v);//建图
    }
    Count=;
    dfs();//从加点1开始搜索标记

    for(int i=;i<=n;i++){
        val[i]=;
    }
    //如果用add(i，1)的话会超时的，只能求出来每个的值，直接初始化
    // c[i]=i-(i-(lowbit(i)) );
    // 就是从1到i的苹果数减去距离i点最近的左侧的树上苹果的数量
    for(int i=;i<=Count;i++){
        lowbit[i]=i&(i^(i-));
    }
    for(int i=;i<=Count;i++){
        c[i]=i-(i-lowbit[i]);
    }//初始状态下每个节点都有一个苹果
    scanf("%d",&m);
    for(int i=;i<m;i++){
        scanf("%s%d",str,&u);
        if(str[]=='C'){
            if(val[u]){
                add(Start[u],-);
                add(End[u],-);
                val[u]=;
            }else{
                add(Start[u],);
                add(End[u],);
                val[u]=;
            }
        }else{
            int x1=sum(End[u]);
            int x2=sum(Start[u]);
            printf("%d\n",(x1-x2)/+val[u]);
        }
    }
    return ;
}