【BZOJ 1001】狼抓兔子 对偶图+SPFA

　　这道题是求图的最小割，也就是用最大流。但因为边太多，最大流算法会T，因此不能用最大流算法。

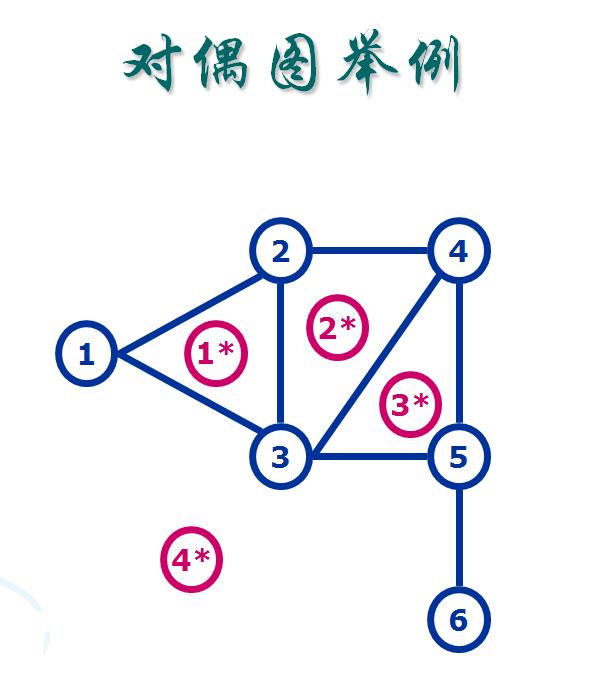
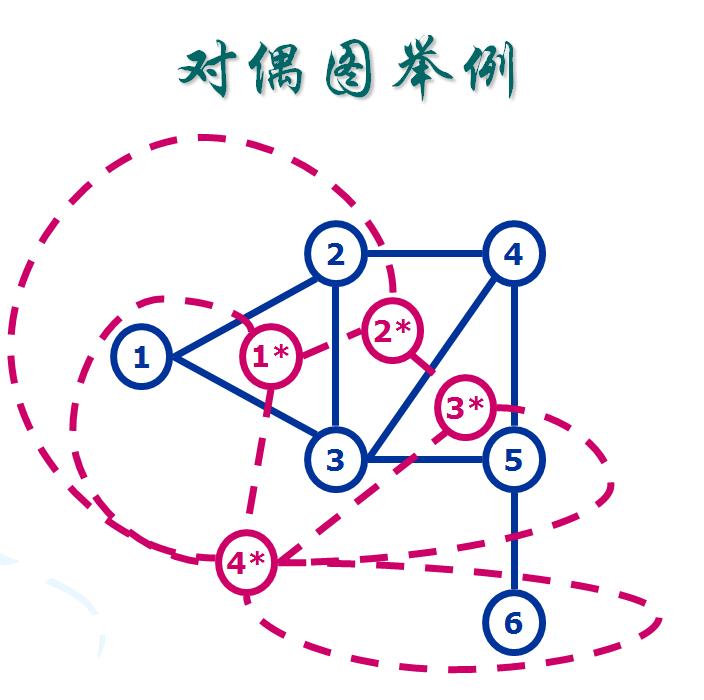
　　因为这是个平面图，所以求平面图的最小割可以使用特殊的技巧就是求对偶图然后求对偶图的最短路。把每个面看成一个点f*，f*之间边的权值就是之前原来的点f之间与f*的边交叉的边的权值。（说的不清楚，大家可以看其他博客，讲得都很好）

　　这样建了一个对偶图G*，由此可见，对偶图G*的一条路对应着原图G的一个割。所以求G*的最短路就相当于求G的最小割。

　　以后遇到平面图求最小割就把它转化成对偶图再求最短路，这样时间效率会大大提高。

88732 kb

3572 ms

C++/Edit

2195 B

 #include<queue>
 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 using namespace std;
 int point[],next[],v[],c[];
 int cnt=,s,t,n,m,dist[];
 bool vis[];
 queue<int>q;
 void insect(int x,int y,int z)
 {cnt++;next[cnt]=point[x];point[x]=cnt;v[cnt]=y;c[cnt]=z;}
 void in1()
 {
     int i,j,num;
     for (j=;j<m;++j)
     {
         scanf("%d",&num);
         insect(j*,t,num);
         insect(t,j*,num);
     }
     for (i=;i<n;++i)
      for (j=;j<m;++j)
      {
          scanf("%d",&num);
          insect((i-)*(m-)*+j*,(i-)*(m-)*+j*-m*+,num);
          insect((i-)*(m-)*+j*-m*+,(i-)*(m-)*+j*,num);
      }
     for (j=;j<m;++j)
     {
         scanf("%d",&num);
         insect(s,(n-)**(m-)+j*-,num);
         insect((n-)**(m-)+j*-,s,num);
     }
 }
 void in2()
 {
     int i,j,num,xx;
     for (i=;i<n;++i)
     {
         scanf("%d",&num); xx=(i-)*(m-)*+;
         insect(s,xx,num);
         insect(xx,s,num);
         for (j=;j<m;++j)
         {
             scanf("%d",&num); xx+=;
             insect(xx-,xx,num);
             insect(xx,xx-,num);
         }
         scanf("%d",&num);
         insect(xx+,t,num);
         insect(t,xx+,num);
     }
 }
 void in3()
 {
     int i,j,num;
     for (i=;i<n;++i)
      for (j=;j<m;++j)
      {
          scanf("%d",&num);
          insect((i-)*(m-)*+j*-,(i-)*(m-)*+j*,num);
          insect((i-)*(m-)*+j*,(i-)*(m-)*+j*-,num);
      }
 }
 void init()
 {
     scanf("%d %d\n",&n,&m);
     s=; t=(n-)*(m-)*+;
     in1();
     in2();
     in3();
 }
 void spfa()
 {
     int num,mp;
     dist[s]=;
     q.push(s);
     while (!q.empty())
     {
         num=q.front(); q.pop(); vis[num]=;
         mp=point[num];
         while (mp>)
         {
             if (dist[v[mp]]>dist[num]+c[mp])
             {
                 dist[v[mp]]=dist[num]+c[mp];
                 if (vis[v[mp]]==)
                 {
                     vis[v[mp]]=; q.push(v[mp]);
                 }
             }
             mp=next[mp];
         }
     }
     printf("%d\n",dist[t]);
 }
 int main()
 {
     memset(dist,,sizeof(dist));
     memset(point,,sizeof(point));
     memset(next,,sizeof(next));
     memset(vis,,sizeof(vis));
     memset(v,,sizeof(v));
     init();
     spfa();
     return ;
 }

　　•平面图性质

　　1.（欧拉公式）如果一个连通的平面图有n个点，m条边和f个面，那么f=m-n+2

　　2.每个平面图G都有一个与其对偶的平面图G*n，G*中的每个点对应G中的一个面n