自定义函数（Power Query 之 M 语言）

数据源：

任意工作簿

目标：

使用自定义函数实现将数据源导入Power Query编辑器

操作过程：

PowerQuery编辑器》主页》新建源》其他源》空查询

编辑栏内写入公式》调用

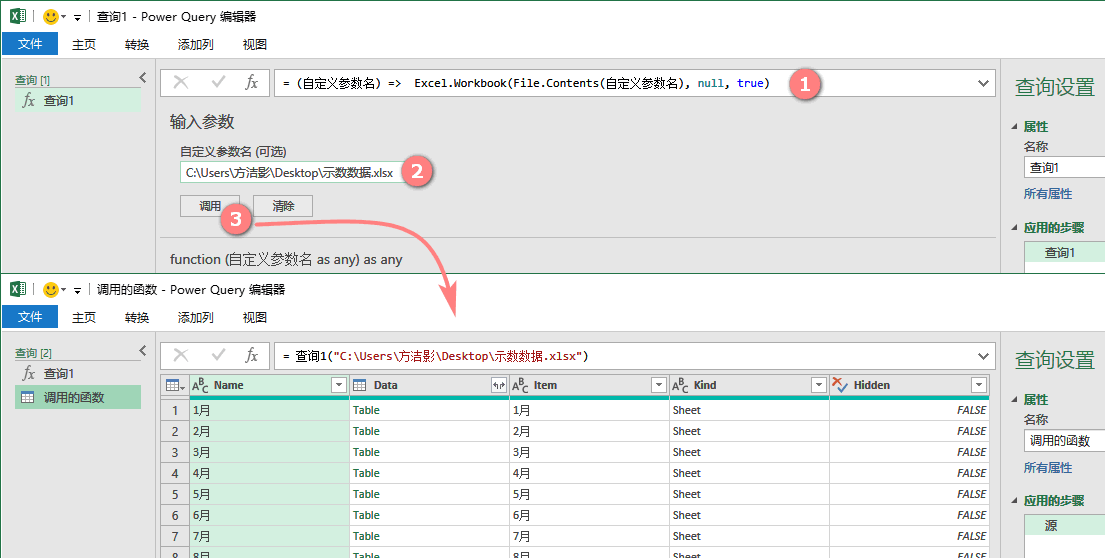
M公式：

= (自定义参数名) => Excel.Workbook(File.Contents(自定义参数名), null, true)

固定结构：

M公式

　　= (参数1,...,参数n) => 包含参数的表达式

M代码（生成自定义函数）

(参数1,...参数n) =>

let

    步骤名 = 包含参数的表达式

in

    步骤名

M代码（返回结果）

　　let

　　　　函数名 = (参数1,...参数n) => 包含参数的表达式,

　　　　步骤名 = 函数名( 参数值1,...,参数值n)

　　in

　　　　步骤名