热身训练2 Another Meaning

题目来源

简要题意：

众所周知，在许多情况下，一个词语有两种意思。比如“hehe”，不仅意味着“hehe”，还意味着“excuse me”。

现在，某某在和妹纸在线聊天，妹纸发送了一个句子A给某某。某某很聪明，知道这个句子中的词语B有两种意思。他想知道妹纸有多少种可能想表达的意思。

分析：

我们令可替换意思的字符串为key，长度为length。

如果我们知道key在原字符串内的哪些地方出现过，即mk[起点]=1。

我们很容易想到一个dp式子

f[i]=f[i-1];

if(mk[i-length+1] == 1) f[i] += f[i-length];

现在，我们只需要能够快速滴求出mk数组即可

KMP！！！yyds！！！

先贴一个kmp的模板，其中la为主串的长度，lb为模式串的长度

    for(re i=2, j=0;i<=lb;++i)
    {
        while(j && b[i] != b[j+1]) j=kmp[j];
        if(b[j+1] == b[i]) j++;
        kmp[i]=j;
    }
    for(re i=1, j=0;i<=la;++i)
    {
        while(j && b[j+1] != a[i]) j=kmp[j];
        if(b[j+1] == a[i]) j++;
        if(j == lb)
        {
            j=kmp[j];
            mk[i-lb+1]=1;
        }
    }

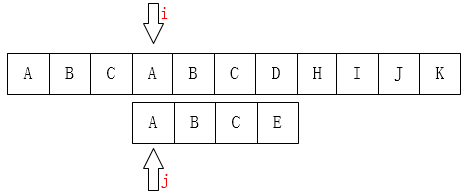
kmp精髓：利用已经部分匹配这个有效信息，保持i指针不回溯，通过修改j指针，让模式串尽量地移动到有效的位置。 

推荐大家去看一下这个有关kmp的博客！

好啦，这道题我们已经会切了哟！

总结一下：

1.我们用kmp，求出模式串在哪里出现过。

2.用dp推出情况总数。

#include<bits/stdc++.h>
using namespace std;
#define re register int
#define int long long
const int N=1e5+5, mo=1e9+7;
char a[N], b[N];
int la, lb, kmp[N], mk[N], f[N];
inline void work()
{
    memset(mk, 0, sizeof(mk));
    a[0]='\0';
    b[0]='\0';
    memset(a, 0, sizeof(a));
    memset(b, 0, sizeof(b));
    cin>>a+1;
    cin>>b+1;
    la = strlen(a+1);
    lb = strlen(b+1);
    for(re i=2, j=0;i<=lb;++i)
    {
        while(j && b[i] != b[j+1]) j=kmp[j];
        if(b[j+1] == b[i]) j++;
        kmp[i]=j;
    }
    for(re i=1, j=0;i<=la;++i)
    {
        while(j && b[j+1] != a[i]) j=kmp[j];
        if(b[j+1] == a[i]) j++;
        if(j == lb)
        {
            j=kmp[j];
            mk[i-lb+1]=1;
        }
    }
    f[0]=1;
    for(re i=1;i<=la;++i)
    {
        f[i] = f[i-1];
        if(i-lb >=0 && mk[i-lb+1])
        {
            f[i] = (f[i] + f[i-lb]) % mo;
        }
    }
    cout<<f[la]<<endl;
}
signed main()
{
    ios::sync_with_stdio(false);
    int T; cin>>T;
    for(re i=1;i<=T;++i)
    {
        cout<<"Case #"<<i<<": ";
        work();
    }
    return 0;
}

“我还是从前那个少年，没有一丝丝改变。”

“时间只不过是考验，种在心中信念丝毫未减。”----《少年》梦然