KMP算法思路

题目

给定一个字符串\(S\),求\(M\)字符串是否是\(S\)字符串中的子串.如果是,返回\(M\)对应\(S\)的第一个下标,否则返回-1.

例如:S串为a b c d a b c d a b c d e

M串为a b c d e

结果:返回S串下标8.

个人想法

之前看过这种求子串的题,但是只在脑海中想象了一下,没有动手写出算法.

看到的时候心里就嘀咕肯定不能暴力求解,需要让子串\(M\)进行跳跃,但是没有具体地研究边界问题,也没有动手写一个字符串验证想法,导致想法很不靠谱.

之前的想法很粗糙:

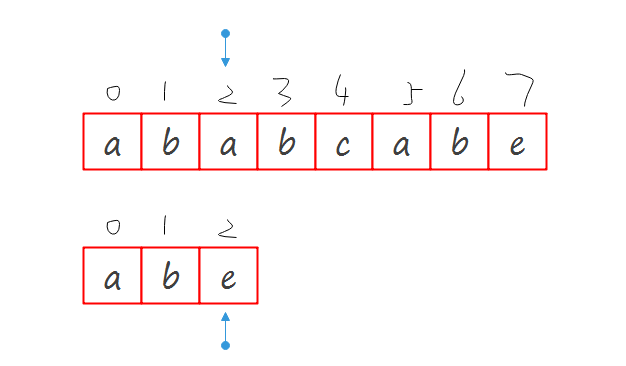
挨个比较字符串,如果不相同,整体都跳跃,跳跃的方式是\(M\)串首位对其不匹配\(S\)串的下标位置.然后继续比较

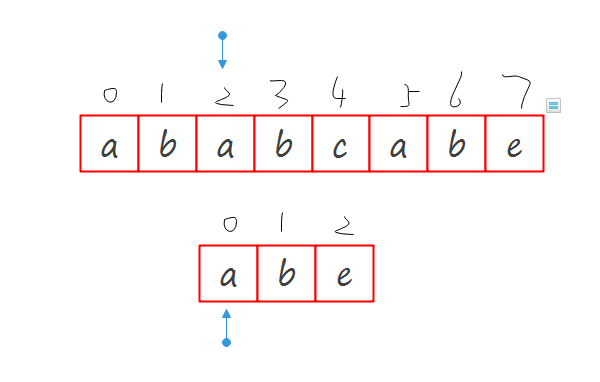
大约就是这个样子,想到这就没继续往下想也没有去实现,这显然是错误的.跳跃是应该跳跃,但是不是那么粗糙的跳跃,假如字符串和子串是下面这种情况这种情况:

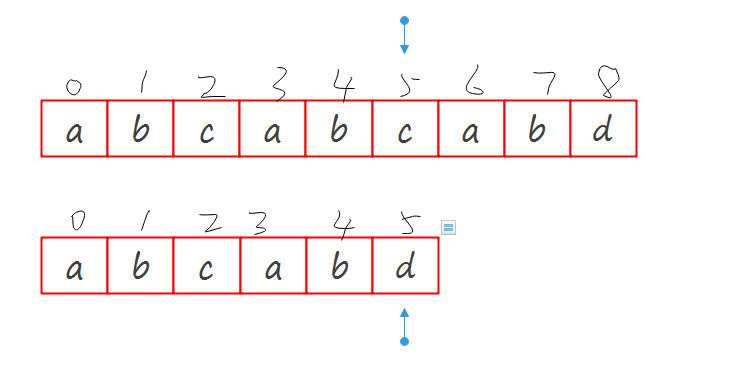
以我那种错误的想法是会产生bug的:

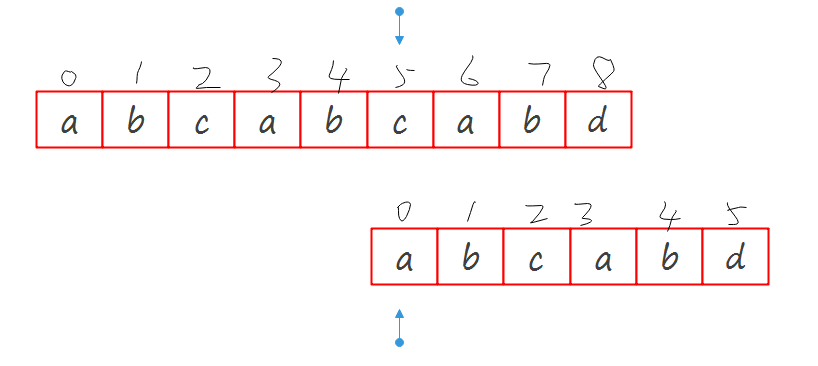
结果是\(S\)串不会包含\(M\)串,但事实上是包含的.(下文将目标串统一称作\(S\),子串统一称作\(M\))

那我们就应该考虑如何正确的跳跃.

KMP算法

知道了之前的想法是错误的,我们就应该找到符合各种边界的跳跃方式.只要确定了跳跃方式,KMP就很容易写出来了.KMP中提到了前缀表(或者最大相同前后缀)这些概念.前缀表暂时先不考虑,只谈谈如何进行跳跃才能满足边界.

继续回到之前的图,如果我们想要成功地找到下标,正确的跳跃方式应该是下图这样:

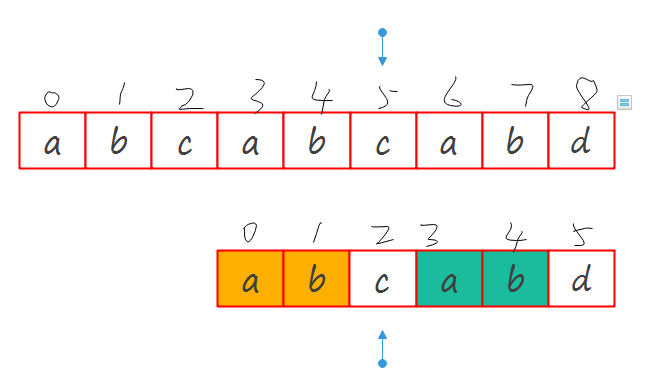
注意\(M\)串错误匹配项(\(M[5]\)元素d)之前的元素(蓝色填充的a,b).

好,为什么这么跳呢?

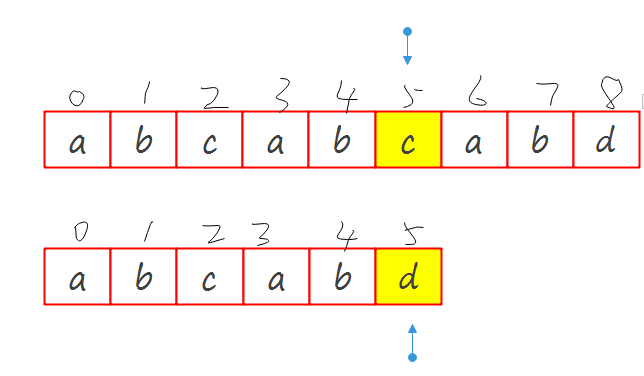
当确定\(S[5]\)和\(M[5]\)不匹配的时候,我们可以确定d之前的项都是匹配的.即\(S[0-4]\)和\(M[0-4]\)是匹配的.

​ \(M[0-4]\)

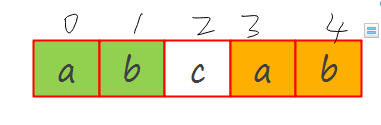
对于已经匹配的\(M[0-4]\),前缀几项与后缀几项相同(即\(M[0]\),\(M[1]\)和\(M[3]\),\(M[4]\)是相同的),那么把\(M\)平移使\(M[0]\)对齐\(M[3]\)之前所处的位置,这一定能确保\(M[0]\),\(M[1]\)和之前\(M[3]\),\(M[4]\)与\(S\)对应的\(S[3]\),\(S[4]\)是匹配的,即一定能确保\(M[0]\),\(M[1]\)和\(S[3]\),\(S[4]\)是匹配的.

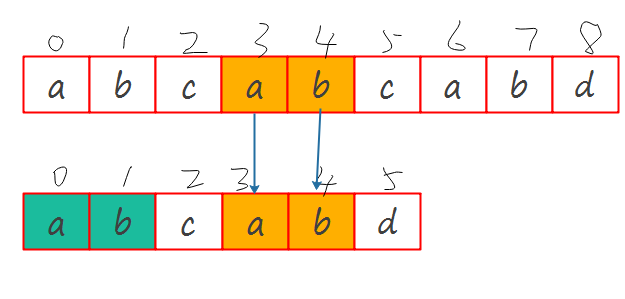
平移

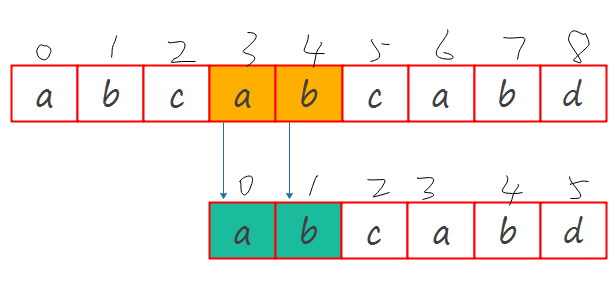
那我们如何利用这个特点跳跃呢,现在我们生成一个辅助的前后缀相同的数组.

以a,b,c,a,b,d为例,

M产生的子串	相同前后缀个数	备注:就把相同前后缀数组称为\(D\)
a	0
a,b	0
a,b,c	0
a,b,c,a	1
a,b,c,a,b	2
a,b,c,a,b,d	0	最后一个匹配就可以返回了,所以用处不大

最后生成一个相同前后缀的数组可以与\(M\)对应起来

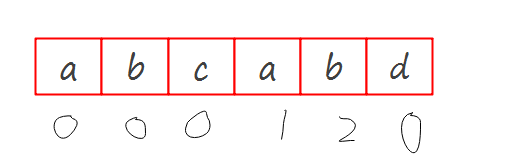
现在只需要解释一下如何使用相同前后缀数组进行跳跃,应该就能写出KMP的代码了.

当\(M[5]\)与\(S[5]\)不相同时,看一下前后缀数组\(D\)前一个位置的值,即\(D[4]\)的值为2,那么只需要将\(M[2]\)平移至\(M[5]\)的位置上就可以了.如果\(M[3]\)不匹配,后缀数组\(D\)的前一位\(D[2]\)是0,那么就把\(M[0]\)平移对其\(M[3]\)的位置就可以了.

假如\(M[0]\)不匹配的话,就直接往后跳一位,与\(S\)下一项比较.

KMP代码实现(JAVA)

整体思路就大致如此了,如果理解了应该可以按照思路写出代码了.

下面就贴一下代码实现,我只是简单地测试了一下,没有大量测试,但是整体思路应该大致如此,可能有些边界问题还没有考虑周全,欢迎指正.

	public static int getIndexOf(String s, String m) {
        if (s == null || m == null || m.length() < 1 || s.length() < m.length()) return -1;
        char[] ss = s.toCharArray(), ms = m.toCharArray();
        int si = 0, mi = 0;
        int[] next = getMatchArray(ms);
        int q = next[mi];
        while (si < ss.length && mi < ms.length) {
            if (ss[si] == ms[mi]) {
                si++;
                mi++;
            } else {
                if (mi != 0) {
                    mi = next[mi - 1];
                } else {
                    si++;
                }
            }
        }
        return mi == ms.length ? si - mi : -1;
    }

    public static int[] getMatchArray(char[] ms) {
        if (ms.length == 1) return new int[]{0};
        int[] next = new int[ms.length];
        next[0] = 0;
        int j = 0, tail = 1;
        while (tail < ms.length) {
            j = next[tail] = ms[j] == ms[tail] ? (j + 1) : 0;
            tail++;
        }
        return next;
    }

    public static void main(String[] args) {
        String str = "abcabcababaccc";
        String match = "ababa";
        System.out.println(getIndexOf(str,match));
    }