Atcoder Typical DP Contest S - マス目（状压 dp+剪枝）

洛谷题面传送门

介绍一个不太主流的、非常暴力的做法（

首先注意到 \(n\) 非常小，\(m\) 比较大，因此显然以列为阶段，对行的状态进行状压。因此我们可以非常自然地想到一个非常 trivial 的做法：\(dp_{i,mask1,mask2}\) 表示考虑到第 \(i\) 列，当前列状态为 \(mask1\)，当前列中能从左上角到达的点集为 \(mask2\)，枚举下一列状态简单转移一下即可。

但是相信聪明的读者到这里一定可以发现，这个做法是错误的，因为题目规定可以朝四个方向走，也就是说有可能出现如下图所示的情况：

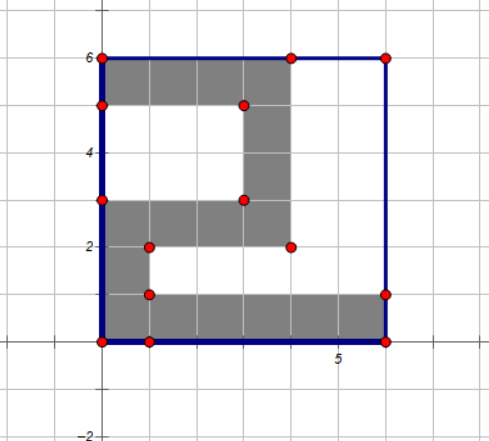
对于下图中的情况，当我们状态转移到第四列时，我们会判定 \(1,2,3,4\) 行是可以从起点到达的，而由于前一列（第 \(3\) 列）的第 \(6\) 行在前三行组成的子矩形中无法从起点到达，因此我们也会判断第四列第 \(6\) 行无法从源点到达，也就导致了情况的漏算。

怎么处理呢？由于这种情况的存在，我们要在状态中多记录一些东西，注意到这个 \(n=6\) 有点小的出奇，\(\dbinom{6}{2}\) 不过 \(15\)，因此考虑对每个点对 \((j,k)\) 记录当前列中这两行的格子在前 \(i\) 列组成的子矩形中是否连通，即设 \(dp_{i,j,k}\) 表示前 \(i\) 列中两两可达性为 \(j\)，\(k\) 中的格子可以从 \((1,1)\) 到达的方案数。这样一来我们在枚举下一列状态并 check 每个点是否能从 \((1,1)\) 到达时可以考虑这样的做法：对于每个 \(j\)，如果它左边的格子能从 \((1,1)\) 到达并且它是黑格，那么它能从 \((1,1)\) 到达，否则如果 \(\exists k\) 满足 \((j,k)\) 在前 \(i\) 列组成的子矩形中连通并且 \(k\) 能从 \((1,1)\) 到达，那么 \(j\) 能从 \((1,1)\) 到达，正确性显然。而显然如果我们知道了上一列的两两之间的可达性，是可以用传递闭包 or 并查集直接推出上一列的可达性的，因此这个做法恰好能够解决我们之前遇到的问题。

复杂度？最坏情况下该算法的复杂度可以达到 \(2^{15}\times 2^6\times 2^6\times 100\times 6^3\approx 3\times 10^{12}\)（这要是能过我就当场把这个电脑屏幕 **），然鹅这个复杂度是远远达不到上界的，因为首先对于这 \(2^{15}\) 个表示可达性的状态中，一个状态合法当且仅当它的传递闭包就是它本身，暴力枚举一下可知这 \(2^{15}\) 个状态中总共只有 \(203\) 个合法的状态，这下复杂度降到了 \(203\times 2^6\times 2^6\times 100\times 6^3\approx 2\times 10^{10}\)，其次在 DP 过程中很多状态是转移不到的，因此如果某个 \(dp_{i,j,k}=0\) 那么我们就不用转移了，加上这个小小的优化之后速度又能快不少。此题 \(\text{TL}=8\text{s}\)，而我这个做法只跑了 \(222\text{ms}\)。当然这肯定不是最快的版本，还有优化的空间，比方说一开始大可不必 \(\mathcal O(2^{15}\times 6^3)\) 枚举所有状态，可以一遍 DFS 一遍把不合法的状态剪掉，这样程序还可以跑得更快（虽然这不是复杂度瓶颈所在），以及在转移中，由于本题的图是无向图，传递闭包可以用 dsu 来代替，这样可将 \(6^3\) 变成 \(6^2\)，但由于本人懒癌症晚期就没有进一步优化了（

const int MAXM=100;
const int MAXT=1<<6;
const int MAXP=1<<15;
const int MAX_ST=203;
const int MOD=1e9+7;
void add(int &x,int v){((x+=v)>=MOD)&&(x-=MOD);}
int n,m,id[MAXP+5],msk[MAXP+5],cnt=0,is[8][8],pre_is[8][8],blk[8];
int dp[MAXM+5][MAXT+5][MAX_ST+5];
int main(){
	scanf("%d%d",&n,&m);int lim=1<<(n*(n-1)/2);
	for(int i=0;i<lim;i++){
		int cur=i;bool flg=1;
		for(int j=1;j<=n;j++) for(int k=1;k<j;k++)
			is[j][k]=is[k][j]=cur&1,cur>>=1;
		for(int j=1;j<=n;j++) is[j][j]=1;
		for(int j=1;j<=n;j++) for(int k=1;k<=n;k++) for(int l=1;l<=n;l++)
			if(is[j][k]&&is[k][l]&&!is[j][l]) flg=0;
		if(flg) msk[++cnt]=i,id[i]=cnt;
	} //printf("%d\n",cnt);
	for(int i=0;i<(1<<n);i++){
		if(~i&1) continue;
		int pre=0,msk1=0,msk2=0;memset(is,0,sizeof(is));
		for(int j=1;j<=n;j++){
			if(~i>>(j-1)&1){
				for(int k=pre+1;k<j;k++) for(int l=pre+1;l<k;l++) is[k][l]=is[l][k]=1;
				if(!pre) for(int k=pre+1;k<j;k++) msk1|=(1<<k-1);
				pre=j;
			}
		} if(!pre) msk1=(1<<n)-1;
		for(int k=pre+1;k<=n;k++) for(int l=pre+1;l<k;l++) is[k][l]=1;
		for(int k=n;k;k--) for(int l=k-1;l;l--) msk2=msk2<<1|is[k][l];
//		printf("%d %d\n",msk1,msk2);
		add(dp[1][msk1][id[msk2]],1);
	}
	for(int i=1;i<m;i++){
		for(int j=1;j<(1<<n);j++){
			for(int k=1;k<=cnt;k++){
//				printf("%d %d %d %d\n",i,j,k,dp[i][j][k]);
				if(!dp[i][j][k]) continue;int cur=msk[k];
				for(int l=1;l<=n;l++) for(int o=1;o<l;o++)
					pre_is[l][o]=pre_is[o][l]=cur&1,cur>>=1;
				for(int l=0;l<(1<<n);l++){
					for(int o=1;o<=n;o++) blk[o]=l>>(o-1)&1;
					int pre=0;memset(is,0,sizeof(is));
					for(int o=1;o<=n;o++){
						if(!blk[o]){
							for(int p=pre+1;p<o;p++) for(int q=pre+1;q<p;q++)
								is[p][q]=is[q][p]=1;
							pre=o;
						}
					}
					for(int p=pre+1;p<=n;p++) for(int q=pre+1;q<p;q++)
						is[p][q]=is[q][p]=1;
					for(int p=1;p<=n;p++) if(blk[p])
						for(int q=1;q<p;q++) if(blk[q])
							is[p][q]|=pre_is[p][q],is[q][p]|=pre_is[q][p];
					for(int p=1;p<=n;p++) if(blk[p])
						for(int q=1;q<=n;q++) if(blk[q])
							for(int r=1;r<=n;r++) if(blk[r])
								is[q][r]|=is[q][p]&is[p][r];
					int msk1=0,msk2=0;
					for(int p=1;p<=n;p++){
						bool flg=0;
						if(blk[p]&&(j>>p-1&1)) flg=1;
						else if(blk[p]){
							for(int q=1;q<=n;q++) if(is[p][q]&&(j>>q-1&1))
								flg=1;
						} msk1|=flg<<(p-1);
					}
					for(int p=n;p;p--) for(int q=p-1;q;q--)
						msk2=msk2<<1|is[p][q];
//					printf("%d %d %d -> %d %d %d(%d)\n",i,j,msk[k],i+1,msk1,msk2,id[msk2]);
					add(dp[i+1][msk1][id[msk2]],dp[i][j][k]);
				}
			}
		}
	} int ans=0;
	for(int j=1;j<(1<<n);j++) if(j>>(n-1)&1)
		for(int k=1;k<=cnt;k++) add(ans,dp[m][j][k]);
	printf("%d\n",ans);
	return 0;
}