如何将声学的spectrogram（声谱图）重新反变换成时域语音信号

最近在研究一些信号分析的事情，感兴趣如何将频谱信号反变换成时域信号。fft 与ifft可以顺畅的转变，但是这个是一帧信号，当时间较长的信号再一起是，通过反变换变成一帧一帧的时域信号，如何把他们拼接起来非常感兴趣，以后会做一些尝试，这里先留个档案。

1.将声音转化为声谱图（Spectrogram）

通过短时傅里叶变换。

2.将声谱图转换为声音

1. 通过ifft将一帧一帧的FFT信号（即1维的FFT信号数组X(F)(i)[ i=0 to length( X(f) ) ]）变换成一小段一小段的时域信号，再将他们拼接起来。（加窗和overlap是否带来影响及相位是否丢失？）

下面打算通过labview或matlab去实现。(本来想查阅了相关资料借鉴一下，没有找到相关的资料，所以打算自己去尝试下下面的处理，如果有知道的还请告诉我相关的资料或方法，借鉴一下，谢谢)

第一步是找一个语音信号，将其转换为STFT的Spectrogram,

第二步是将他还原回去一帧一帧的声学信号，并拼接成语音信号，看语音信号是否能1. 语音是否能还原，2平滑过渡，3相位是否会丢失。（2019-12-15，完成后再来更新）

2019-12-05 当天使用Labview 尝试了一下。今天公司圣诞放假，有空更新一下 （2019-12-25）

1.找了windows里一段语音 alarm.wav 时域信号如下

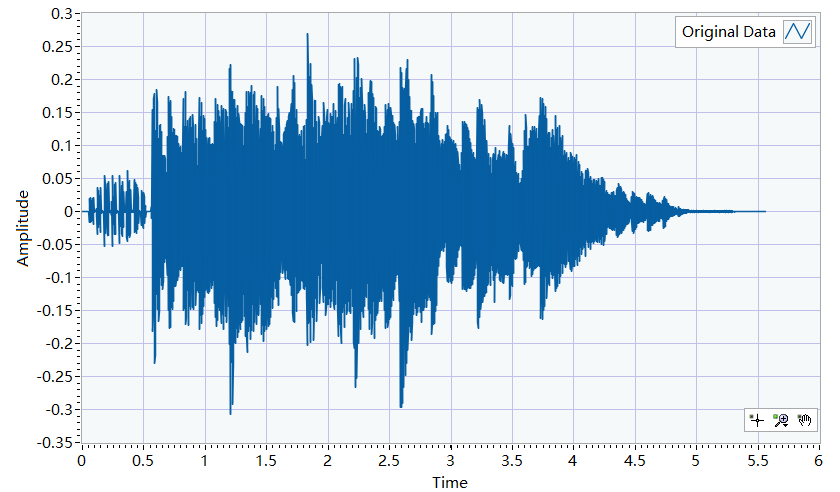
图1. 音频时域图

通过labview 中的STFT 函数进行频谱分析。

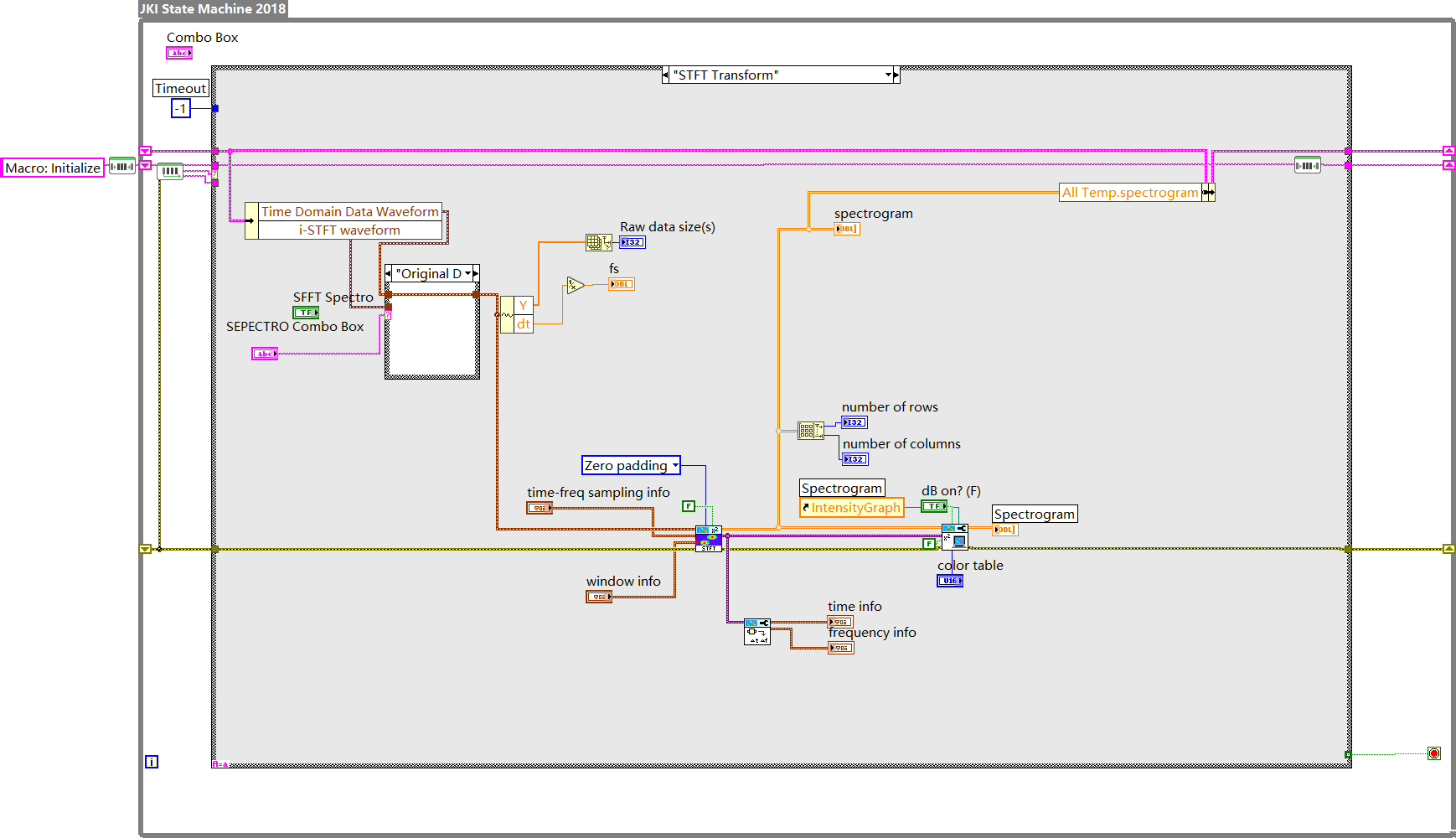
图2. STFT 函数图

其中关于STFT函数

 

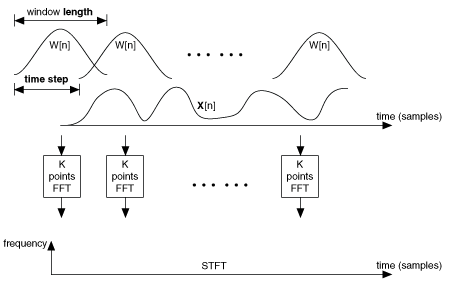
Labview 中STFT分几个步骤

1. K points 由 frquency bins 决定。即每次截取K个点，此例中8192个点。决定了FFT后的截止频率为1/2* frequency bins;

2. 加窗函数，类型 Type 这里使用汉宁窗，length 决定了数据点在长度范围外为0值

3. time step 决定了数据块往前进的速度，他与加窗length,共同决定了数据块中overlap的值

得到图3 STFT 声谱图，实际是一个2维数组。

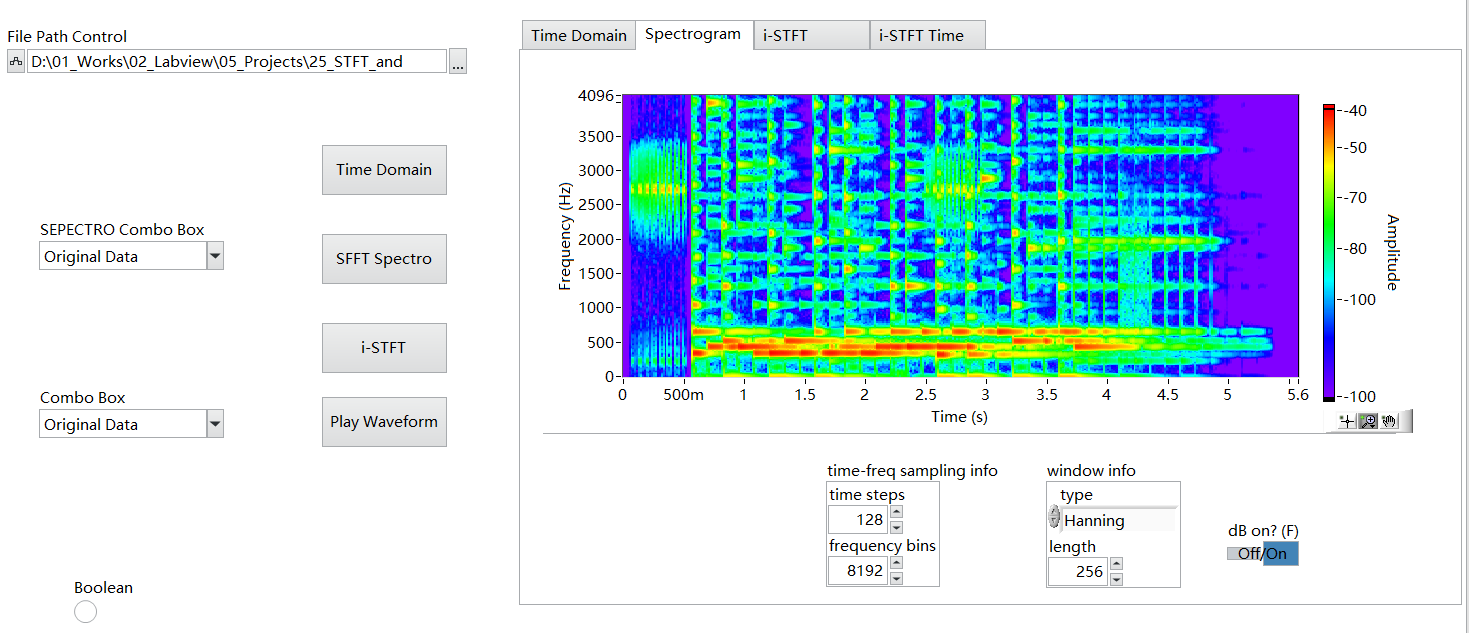
图3. STFT 声谱图

尝试将这个2D数组还原成时域音频信号，看是否能够高保真还原。

将这个2D数组（i*j大小）的FFT数据依次取出，进行i-fft（FFT 逆变换），得到FFT前的时域信号（此时是时域信号加过窗的数据。）。将这些数据再依次拼接出来，回放声音，发现不对。原来是这些数据1. 加过窗了，2，有重复冗余（OVERLAP的原因），

应该每次从逆变换的时域信号中只取time step个数的数据点，怎么取？假设i-fft后的数据长度为N，则从第（ 1/2*N取整 - 1/2* ( time step length)) 开始，取time step个数。

将j个时域信号的segment依次拼接起来，得到从光谱图转化到的时域信号。从实验的结果来看，这个转化来的时域信号与原始信号相比，还是能听出来的，只是有一些失真，我的分析是由于加窗带来的，因为i-fft后得到的是原始信号*窗函数的信号，这里我并没有将原始信号还原出来，主要是我尝试了下，除以窗函数，并没有效，所以还有待研究。

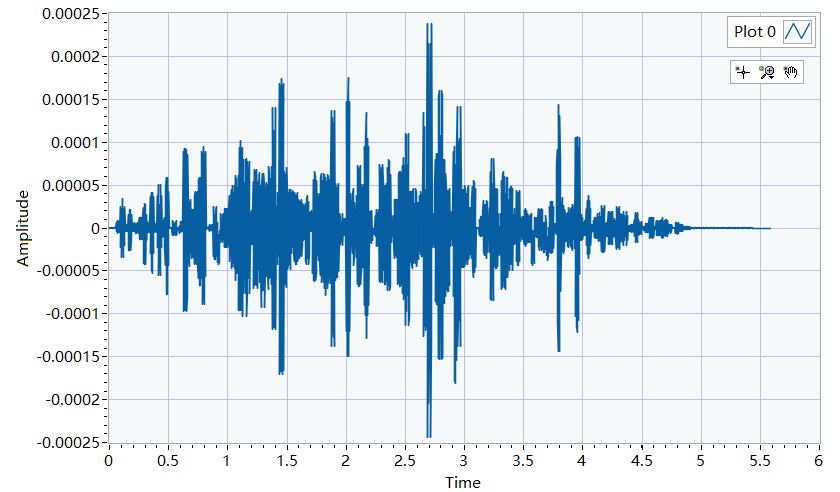
图4. 声谱图通过i-fft还原的声信号（能听出来原始信号的内容，但略失真，失真程度受频谱图分析的 window length, time step ，frequency bins影响 ）。

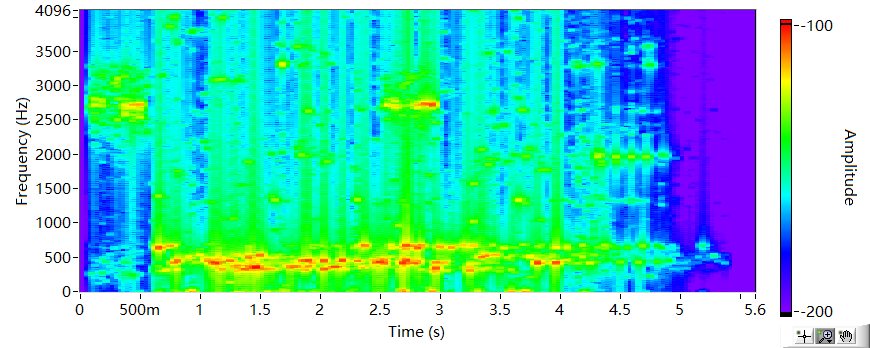
图4. 将i-fft还原的声信号再次做STFT得到的声谱图。

下面会继续研究，去除加窗函数的影响。

2020-01-01 更新

弄明白了一件事，就是短时傅里叶时， 生成的spectrogram 是X^2的信号，也就是说是复数的平方，丢失了相位信息，所以在上面做STFT逆变换时会有些失真（相位信息不对）。

如果使用STFT时，生成的colormap 是coef 矩阵（复实数）时，可以反变换成时域信号而不失真。

感觉利用这个性质，可以做一些阈值滤波与信号增强。后续进行研究。