BZOJ4034: [HAOI2015]树上操作

这题把我写吐了。。。代码水平还是太弱鸡了啊。。。

这题就是先给你一些点，以及点权。然后给你一些向边构成一颗树，树的根节点是1。

然后给定三个操作

第一个是把指定节点的权值+W

第二个是把指定节点X为根（包括自己）的所有点权+W

第三个是求出指定节点到根节点的点权之和

嗯没错，听了大佬讲，肯定跑不了是DFS序，那么是用哪种呢？？？是N的还是2N的？？

我们思考一个问题，如果是N的，能表示什么遍历完成儿子节点的时间吗？？？显然不能

但是。。。2n的是可以的，因为节点DFS出现两次中间的节点都是他的儿子。

如果知道DFS序列，上面1.2操作显然是不足为虑的。。。但是3操作呢？？？我们如果单纯求和，那么有些没有走过的点会计算两次，

不妨这样考虑：我们写出DFS序

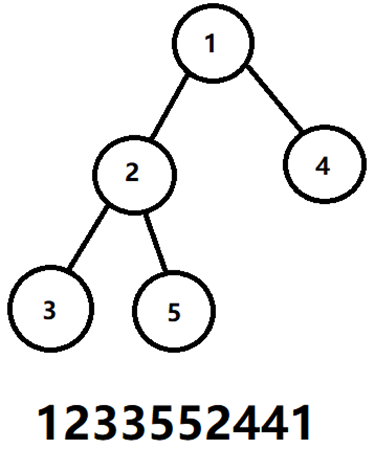
如果求5到根节点，我们会求出12（33）5，每个数前后的位置，我们可以用一个数组存储（这非常简单），我们能不能想办法消去这个影响呢？？？

这是没问题的，我来思考一下，如果我依照某个DFS序，到底起点，那么DFS序中出现两次的一定是没用的，我们统计内部内部只出现一次数的个数，这个些个数就是操作3在这个区间的效果。

但是还有一个问题，我们如果抵消了，那么是不是GG了？我以后访问这个数岂不是也完蛋了？但题目要求跟新的整个子树，我如果这样抵消。。。会对以后造成影响吗？？

其实是不会的，因为我们是把加的值放在了这个数第一次出现的地方，把减的值放在了第二次出现的地方。我们实际上对后面不会有影响，如果要访问节点x以及其子树，一定不会访问到第二个节点x出现的位置。

#include<iostream>
#include<stdio.h>
#include<string.h>
#include<algorithm>
#include<vector>
#define LL long long
using namespace std;
const int maxx = 1e6+;
struct node{
  int l,r;
  LL sum,laze;
}tree[maxx<<];
struct snode{
  int pre,bac;
}id[maxx];
vector<int>G[maxx];
int vis[maxx];
int st[maxx];
int num[maxx],a[maxx],b[maxx],c[maxx];
int n,m;
int cnt;
int num_s;
inline int L(int x){return x<<;};
inline int R(int x){return x<<|;};
inline int MID(int l,int r){return (l+r)>>;};
void push_down(int root){
    if (tree[root].laze){
        tree[L(root)].laze+=tree[root].laze;
        tree[R(root)].laze+=tree[root].laze;
        tree[L(root)].sum+=(LL)(num[tree[L(root)].r]-num[tree[L(root)].l-])*tree[root].laze;
        tree[R(root)].sum+=(LL)(num[tree[R(root)].r]-num[tree[R(root)].l-])*tree[root].laze;
        tree[root].laze=;
    }
}
void buildtree(int root,int l,int r){
     tree[root].l=l;
     tree[root].r=r;
     tree[root].laze=;
     tree[root].sum=;
     if (l==r){
        tree[root].sum=(LL)(num[l]-num[l-])*a[st[l]];
        return;
     }
     int mid=MID(l,r);
     buildtree(L(root),l,mid);
     buildtree(R(root),mid+,r);
     tree[root].sum=tree[L(root)].sum+tree[R(root)].sum;
}
void update(int root,int ul,int ur,int w){
    int l=tree[root].l;
    int r=tree[root].r;
    if (ul<=l && r<=ur){
        tree[root].sum+=(LL)(num[r]-num[l-])*w;
        tree[root].laze+=w;
        return;
    }
    push_down(root);
    int mid=MID(l,r);
    if (ur<=mid){
        update(L(root),ul,ur,w);
    }else if(ul>mid){
        update(R(root),ul,ur,w);
    }else{
        update(L(root),ul,mid,w);
        update(R(root),mid+,ur,w);
    }
    tree[root].sum=tree[L(root)].sum+tree[R(root)].sum;
}
LL query(int root,int ql,int qr){
   int l=tree[root].l;
   int r=tree[root].r;
   int mid;
   LL sum=;
   if (ql<=l && r<=qr){
      return tree[root].sum;
   }
   mid=MID(l,r);
   push_down(root);
   if (qr<=mid){
     sum+=query(L(root),ql,qr);
   }else if (ql>mid){
     sum+=query(R(root),ql,qr);
   }else {
     sum+=query(L(root),ql,mid);
     sum+=query(R(root),mid+,qr);
   }
   return sum;
}
void dfs(int x)
{
    vis[x]=;
    cnt++;
    num[cnt]=;
    st[cnt]=x;
    c[x]=cnt;
    id[x].pre=cnt;
    for (int i=;i<G[x].size();i++)
    {
            if(!vis[G[x][i]]){
            dfs(G[x][i]);
            }
    }
    cnt++;
    id[x].bac=cnt;
    st[cnt]=x;
    num[cnt]=-;
}
int main()
{
    int u,v,op,tmp1,tmp2;
    while(~scanf("%d%d",&n,&m))
    {
        for (int i=;i<=n;i++){
            G[i].clear();
        }
        cnt=;
        num_s=;
        memset(vis,,sizeof(vis));
        memset(tree,,sizeof(tree));
        for (int i=;i<=n;i++){
            scanf("%d",&a[i]);
        }
        for (int i=; i<n; i++)
        {
            scanf("%d%d",&u,&v);
            G[u].push_back(v);
            G[v].push_back(u);
        }
        dfs();
        num[]=;
        for (int i=;i<=*n;i++){
            num[i]=num[i-]+num[i];
        }
        buildtree(,,*n);
        while(m--){
            scanf("%d",&op);
            if (op==){
                scanf("%d%d",&tmp1,&tmp2);
                update(,id[tmp1].pre,id[tmp1].pre,tmp2);
                update(,id[tmp1].bac,id[tmp1].bac,tmp2);
            }else if (op==){
                scanf("%d%d",&tmp1,&tmp2);
                update(,id[tmp1].pre,id[tmp1].bac,tmp2);
            }else {
                scanf("%d",&tmp1);
                printf("%lld\n",query(,,id[tmp1].pre));;
            }
        }
    }
    return ;
}
/*

*/