分类器的评价指标-ROC&AUC

ROC 曲线：接收者操作特征曲线(receiver operating characteristic curve)，是反映敏感性和特异性连续变量的综合指标，roc 曲线上每个点反映着对同一信号刺激的感受性。

对于分类器或者说分类算法，评价指标主要有precision，recall，F1 score等，以及这里要讨论的ROC和AUC。下图是一个 ROC 曲线的示例：

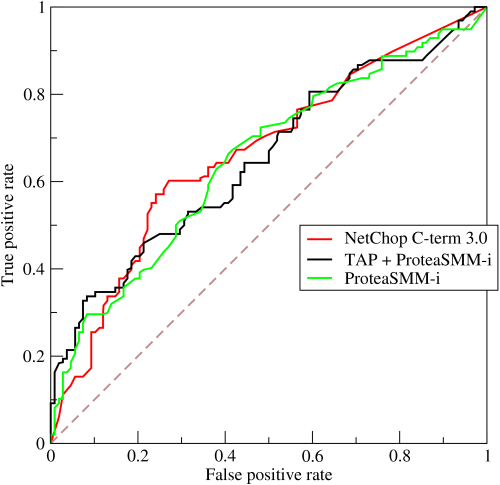
横坐标：Sensitivity，伪正类率(False positive rate， FPR)，预测为正但实际为负的样本占所有负例样本的比例；
纵坐标：1-Specificity，真正类率(True positive rate， TPR)，预测为正且实际为正的样本占所有正例样本的比例。

在一个二分类模型中，假设采用逻辑回归分类器，其给出针对每个实例为正类的概率，那么通过设定一个阈值如 0.6，概率大于等于 0.6 的为正类，小于 0.6 的为负类。对应的就可以算出一组(FPR,TPR)，在平面中得到对应坐标点。随着阈值的逐渐减小，越来越多的实例被划分为正类，但是这些正类中同样也掺杂着真正的负实例，即 TPR 和 FPR 会同时增大。阈值最大时，对应坐标点为(0,0)，阈值最小时，对应坐标点(1,1)。

如下面这幅图，(a)图中实线为 ROC 曲线，线上每个点对应一个阈值。

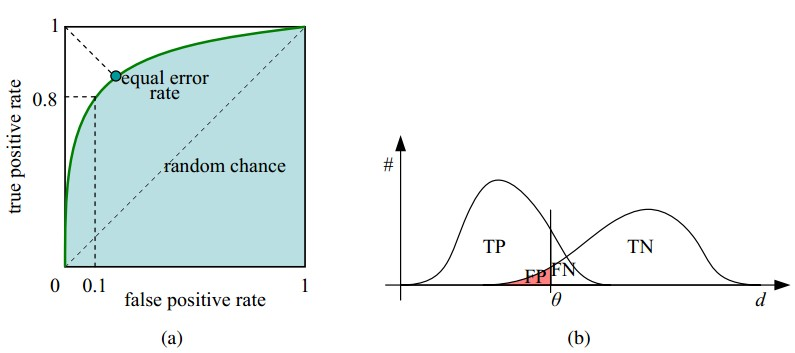
(a) 理想情况下，TPR 应该接近 1，FPR 应该接近 0。ROC 曲线上的每一个点对应于一个 threshold，对于一个分类器，每个 threshold 下会有一个 TPR 和 FPR。比如 Threshold 最大时，TP=FP=0，对应于原点；Threshold 最小时，TN=FN=0，对应于右上角的点(1,1)。
(b) P 和 N 得分不作为特征间距离 d 的一个函数，随着阈值 theta 增加，TP 和 FP 都增加。

横轴 FPR：1-TNR，1-Specificity，FPR 越大，预测正类中实际负类越多。
纵轴 TPR：Sensitivity(正类覆盖率)，TPR 越大，预测正类中实际正类越多。
理想目标：TPR=1，FPR=0，即图中(0,1)点，故 ROC 曲线越靠拢(0,1)点，越偏离 45 度对角线越好，Sensitivity、Specificity 越大效果越好。

随着阈值 threshold 调整，ROC 坐标系里的点如何移动可以参考：

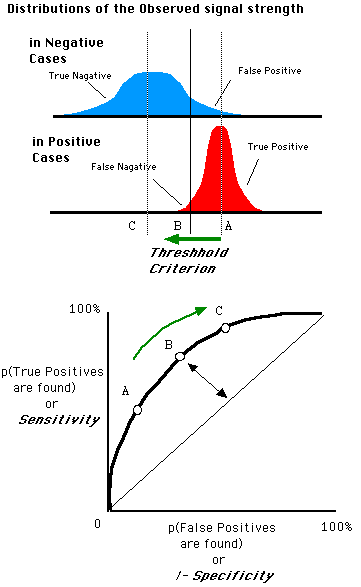
三、如何画 ROC 曲线

对于一个特定的分类器和测试数据集，显然只能得到一个分类结果，即一组 FPR 和 TPR 结果，而要得到一个曲线，我们实际上需要一系列 FPR 和 TPR 的值，这又是如何得到的呢？我们先来看一下 Wikipedia 上对 ROC 曲线的定义：

In signal detection theory, a receiver operating characteristic (ROC), or simply ROC curve, is a graphical plot which illustrates the performance of a binary classifier system as its discrimination threshold is varied.

问题在于“as its discrimination threashold is varied”。如何理解这里的“discrimination threashold”呢？我们忽略了分类器的一个重要功能“概率输出”，即表示分类器认为某个样本具有多大的概率属于正样本（或负样本）。通过更深入地了解各个分类器的内部机理，我们总能想办法得到一种概率输出。通常来说，是将一个实数范围通过某个变换映射到(0,1)区间。

假如我们已经得到了所有样本的概率输出（属于正样本的概率），现在的问题是如何改变“discrimination threashold”？我们根据每个测试样本属于正样本的概率值从大到小排序。下图是一个示例，图中共有 20 个测试样本，“Class”一栏表示每个测试样本真正的标签（p 表示正样本，n 表示负样本），“Score”表示每个测试样本属于正样本的概率。

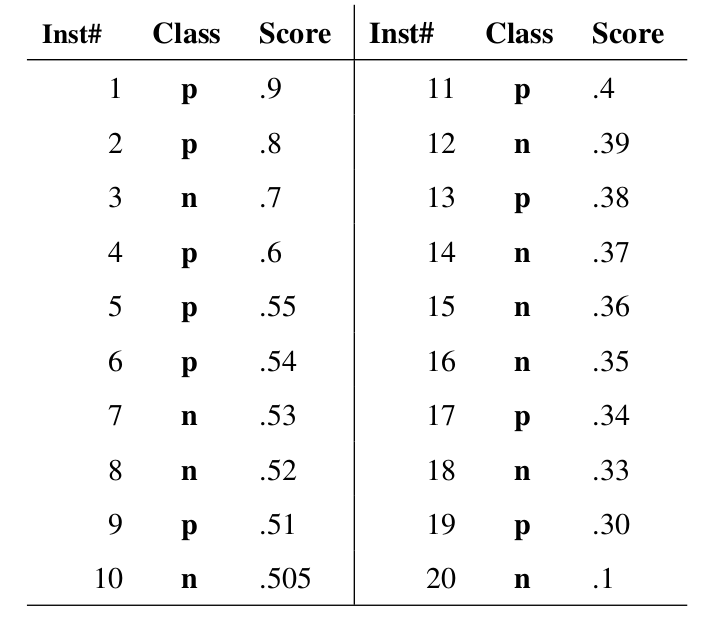
接下来，我们从高到低，依次将“Score”值作为阈值 threshold，当测试样本属于正样本的概率大于或等于这个 threshold 时，我们认为它为正样本，否则为负样本。举例来说，对于图中的第 4 个样本，其“Score”值为 0.6，那么样本 1，2，3，4 都被认为是正样本，因为它们的“Score”值都大于等于 0.6，而其他样本则都认为是负样本。每次选取一个不同的 threshold，我们就可以得到一组 FPR 和 TPR，即 ROC 曲线上的一点。这样一来，我们一共得到了 20 组 FPR 和 TPR 的值，将它们画在 ROC 曲线的结果如下图：

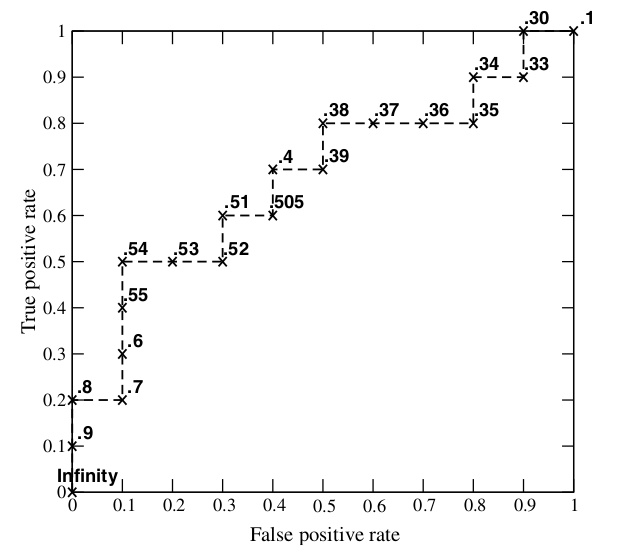
当我们将 threshold 设置为 1 和 0 时，分别可以得到 ROC 曲线上的(0,0)和(1,1)两个点。将这些(FPR,TPR)对连接起来，就得到了 ROC 曲线。当 threshold 取值越多，ROC 曲线越平滑。

其实，我们并不一定要得到每个测试样本是正样本的概率值，只要得到这个分类器对该测试样本的“评分值”即可（评分值并不一定在(0,1)区间）。评分越高，表示分类器越肯定地认为这个测试样本是正样本，而且同时使用各个评分值作为 threshold。我认为将评分值转化为概率更易于理解一些。

四、AUC

AUC 值的计算

AUC (Area Under Curve) 被定义为 ROC 曲线下的面积，显然这个面积的数值不会大于 1。又由于 ROC 曲线一般都处于 y=x 这条直线的上方，所以 AUC 的取值范围一般在 0.5 和 1 之间。使用 AUC 值作为评价标准是因为很多时候 ROC 曲线并不能清晰的说明哪个分类器的效果更好，而作为一个数值，对应 AUC 更大的分类器效果更好。

AUC 的计算有两种方式，梯形法和 ROC AUCH 法，都是以逼近法求近似值，具体见wikipedia。

AUC 意味着什么

那么 AUC 值的含义是什么呢？根据(Fawcett, 2006)，AUC 的值的含义是：

The AUC value is equivalent to the probability that a randomly chosen positive example is ranked higher than a randomly chosen negative example.

这句话有些绕，我尝试解释一下：首先 AUC 值是一个概率值，当你随机挑选一个正样本以及一个负样本，当前的分类算法根据计算得到的 Score 值将这个正样本排在负样本前面的概率就是 AUC 值。当然，AUC 值越大，当前的分类算法越有可能将正样本排在负样本前面，即能够更好的分类。

从 AUC 判断分类器（预测模型）优劣的标准：

AUC = 1，是完美分类器，采用这个预测模型时，存在至少一个阈值能得出完美预测。绝大多数预测的场合，不存在完美分类器。
0.5 < AUC < 1，优于随机猜测。这个分类器（模型）妥善设定阈值的话，能有预测价值。
AUC = 0.5，跟随机猜测一样（例：丢铜板），模型没有预测价值。
AUC < 0.5，比随机猜测还差；但只要总是反预测而行，就优于随机猜测。

三种 AUC 值示例：

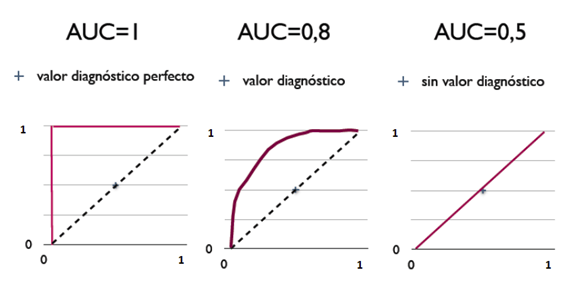
简单说：AUC 值越大的分类器，正确率越高。

为什么使用 ROC 曲线

既然已经这么多评价标准，为什么还要使用 ROC 和 AUC 呢？因为 ROC 曲线有个很好的特性：当测试集中的正负样本的分布变化的时候，ROC 曲线能够保持不变。在实际的数据集中经常会出现类不平衡(class imbalance)现象，即负样本比正样本多很多(或者相反)，而且测试数据中的正负样本的分布也可能随着时间变化。下图是 ROC 曲线和Precision-Recall曲线的对比：

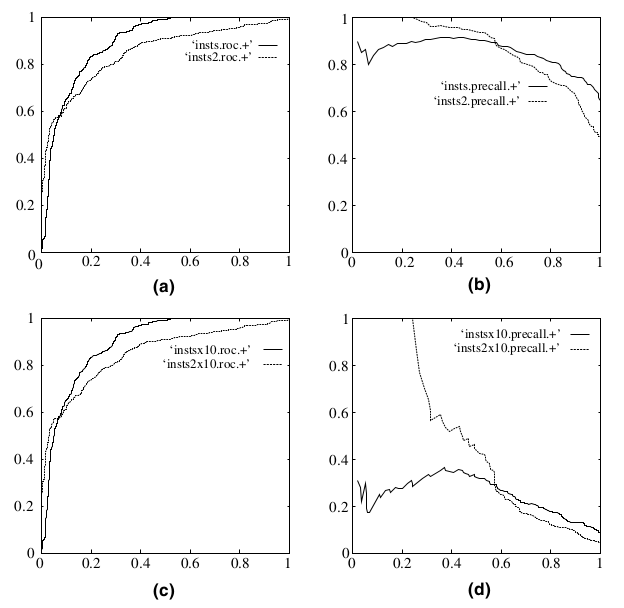
在上图中，(a)和(c)为 ROC 曲线，(b)和(d)为 Precision-Recall 曲线。(a)和(b)展示的是分类其在原始测试集(正负样本分布平衡)的结果，(c)和(d)是将测试集中负样本的数量增加到原来的 10 倍后，分类器的结果。可以明显的看出，ROC 曲线基本保持原貌，而 Precision-Recall 曲线则变化较大。

转载 http://zhwhong.ml/2017/04/14/ROC-AUC-Precision-Recall-analysis/