NOIP2018Day1T2 货币系统

题目描述

在网友的国度中共有 \(n\) 种不同面额的货币，第 \(i\) 种货币的面额为 \(a[i]\)，你可以假设每一种货币都有无穷多张。为了方便，我们把货币种数为 \(n\)、面额数组为 \(a[1..n]\) 的货币系统记作 \((n,a)\)。

在一个完善的货币系统中，每一个非负整数的金额 \(x\) 都应该可以被表示出，即对每一个非负整数 \(x\)，都存在 \(n\) 个非负整数 \(t[i]\) 满足 \(a[i] \times t[i]\) 的和为 \(x\)。然而， 在网友的国度中，货币系统可能是不完善的，即可能存在金额 xx不能被该货币系统表示出。例如在货币系统 \(n=3, a=[2,5,9]\) 中，金额 \(1,3\) 就无法被表示出来。

两个货币系统 \((n,a)\) 和 \((m,b)\) 是等价的，当且仅当对于任意非负整数 \(x\)，它要么均可以被两个货币系统表出，要么不能被其中任何一个表出。

现在网友们打算简化一下货币系统。他们希望找到一个货币系统 \((m,b)\)，满足 \((m,b)\) 与原来的货币系统 \((n,a)\) 等价，且 \(m\) 尽可能的小。他们希望你来协助完成这个艰巨的任务：找到最小的 \(m\)。

输入输出格式

输入文件的第一行包含一个整数 \(T\)，表示数据的组数。

接下来按照如下格式分别给出 TT 组数据。 每组数据的第一行包含一个正整数 \(n\)。接下来一行包含 \(n\) 个由空格隔开的正整数 \(a[i]\)。

输出文件共有 \(T\) 行，对于每组数据，输出一行一个正整数，表示所有与 \((n,a)\) 等价的货币系统 \((m,b)\) 中，最小的 \(m\) 。

输入输出样例

输入样例1:

2
4
3 19 10 6
5
11 29 13 19 17

输出样例1:

2
5

说明

在第一组数据中，货币系统 \((2, [3,10])\) 和给出的货币系统 \((n, a)\) 等价，并可以验证不存在 \(m < 2\) 的等价的货币系统，因此答案为 \(2\) 。 在第二组数据中，可以验证不存在 \(m < n\) 的等价的货币系统，因此答案为 \(5\) 。

【数据范围与约定】

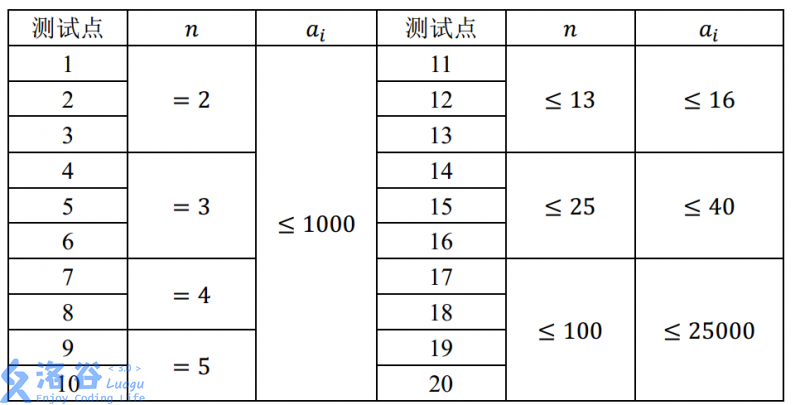
对于 \(100\%\) 的数据，满足 \(1 ≤ T ≤ 20, n,a[i] ≥ 1\)

Solution:

简略题意:给定一个集合 \(A\) 让你找出一个集合 \(B\) 使得 \(A\) 中的所有元素都能被 \(B\) 中的一个和多个元素表示出来 \(,\) 要求 \(B\) 的元素尽量少 \(,\) 求 \(B\) 中最少的元素个数

先排个序 \(,\) 一个数字一定只能由比它本身小的数字通过累加得到 \(,\) 枚举 \(A\) 中的所有元素 \(,\) 然后用判定性完全背包来确定哪一个数字能被表示 \(,\) 每有一个数字能被表示 \(,\) 就把原先等于 \(n\) 的 \(ans--\) 最后输出 \(ans\) 就完了

#include <algorithm>
#include <iostream>
#include <cstring>
#include <cstdlib>
#include <cstdio>

const int N = 1e2 + 10 ;
const int M = 2e4 + 5e3 + 5 ;

int T , a[N] ;
int cnt , n ;
int f[M] ;

int main(){
    scanf ("%d" , & T ) ;
    while ( T -- ){
        scanf ("%d" , & n ) ; memset ( f , 0 , sizeof ( f ) ) ;
        for (int i = 1 ; i <= n ; ++ i) scanf ("%d" , & a[i]) ;
        std::sort ( a + 1 , a + n + 1 ) ; f[0] = 1 ; cnt = n ;// 0 显然可以被任何集合表示
        for (int i = 1 ; i <= n ; ++ i){
            if ( f[a[i]] ) { -- cnt ; continue ; }
            for (int j = a[i] ; j <= a[n] ; ++ j)
                f[j] = f[j] | f[j-a[i]] ; //如果 j-a[i] 能被表示,那么显然j也能被表示
        }
        printf ("%d\n" , cnt ) ;
    }
    system ("pause") ; return 0 ;
}