AI 概率论
概率论
不确定性
量化
频率
频率派
贝叶斯派
1、随机变量(random variable)
随机取不同值的变量,取值可以离散或者连续。
2、概率分布(probability distribution)
描述随机变量每个取值的可能性大小。
离散:概率质量函数(probability mass function,简称PMF)
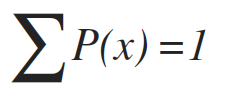
连续:概率密度函数(probability density function,简称PDF)

联合概率分布(joint probability distribution),多个变量的概率分布
边缘概率
条件概率
均匀分布(uniform distribution)
期望(expectation)
方差(variance)
协方差(covariance)
衡量两个变量的相关性。
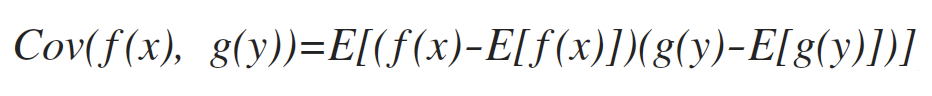
归一化(nomalization)
指数分布
Laplace分布
正态分布
先验概率(prior probability)
后验概率(posterior probability),是一种条件概率。
3、结构化概率模型(structured probabilistic model)/图模型(graphical model)
AI 概率论的更多相关文章
- AI 高等数学、概率论基础
一.概论 基础引入: 原理一:[两边夹定理] 原理二:[极限] X为角度x对应的圆弧的点长: 原理三[单调性]: 引入: 二.导数 常见函数的导数: 四.应用: 求解: 泰勒展式和麦克劳林展式: 泰勒 ...
- 普通程序员如何转向AI方向
眼下,人工智能已经成为越来越火的一个方向.普通程序员,如何转向人工智能方向,是知乎上的一个问题.本文是我对此问题的一个回答的归档版.相比原回答有所内容增加. 一. 目的 本文的目的是给出一个简单的,平 ...
- AI方向
普通程序员如何转向AI方向 眼下,人工智能已经成为越来越火的一个方向.普通程序员,如何转向人工智能方向,是知乎上的一个问题.本文是我对此问题的一个回答的归档版.相比原回答有所内容增加. 一. 目的 ...
- deeplearning.ai 人工智能行业大师访谈 Ian Goodfellow 听课笔记
1. Ian Goodfellow之前是做神经科学研究,在斯坦福上了Andrew NG的课之后,Ian决定投身AI.在寒假他和小伙伴读了Hinton的论文,然后搭了一台用CUDA跑Boltzmann ...
- 普通程序员如何转向AI方向(转)
普通程序员如何转向AI方向 眼下,人工智能已经成为越来越火的一个方向.普通程序员,如何转向人工智能方向,是知乎上的一个问题.本文是我对此问题的一个回答的归档版.相比原回答有所内容增加. 一. 目的 ...
- AI 学习路线
[导读] 本文由知名开源平台,AI技术平台以及领域专家:Datawhale,ApacheCN,AI有道和黄海广博士联合整理贡献,内容涵盖AI入门基础知识.数据分析挖掘.机器学习.深度学习.强化学习.前 ...
- 贝叶斯公式由浅入深大讲解—AI基础算法入门
1 贝叶斯方法 长久以来,人们对一件事情发生或不发生的概率,只有固定的0和1,即要么发生,要么不发生,从来不会去考虑某件事情发生的概率有多大,不发生的概率又是多大.而且概率虽然未知,但最起码是一个确定 ...
- 学习笔记DL008:概率论,随机变量,概率分布,边缘概率,条件概率,期望、方差、协方差
概率和信息论. 概率论,表示不确定性声明数学框架.提供量化不确定性方法,提供导出新不确定性声明(statement)公理.人工智能领域,概率法则,AI系统推理,设计算法计算概率论导出表达式.概率和统计 ...
- 【人工智能】从零开始学好人工智能,AI知识体系和框架
写在前面: 最近公司的业务方向开始向AI方向改变(人工智能+文娱),但是现阶段AI方面的知识还没有储备,所以作为测试,也开始学习这方面的知识,不掉队. 知识储备: 1.阶段一-高等数学 高 ...
随机推荐
- 机器学习实战 - python3 学习笔记(一) - k近邻算法
一. 使用k近邻算法改进约会网站的配对效果 k-近邻算法的一般流程: 收集数据:可以使用爬虫进行数据的收集,也可以使用第三方提供的免费或收费的数据.一般来讲,数据放在txt文本文件中,按照一定的格式进 ...
- Vue学习资料
1. {{ msg }}插值表达式. v-text:将数据插入到页面中,没有闪烁问题. v-cloak:通过style属性选择器的方式display:none:防止闪烁问题. v-html:将标签解析 ...
- linux学习笔记-grub模式引导进入系统
我的邮箱地址:zytrenren@163.com欢迎大家交流学习纠错! 1.设置系统启动盘所在位置 set root='hd0,msdosx' 2.手动加载内核驱动程序并配置root目录位置 linu ...
- [总结]web前端常用JavaScript代码段及知识点集锦
DOM相关 判断浏览器是否支持placeholder属性 function placeholderSupport() { return 'placeholder' in document.create ...
- logo.ico在html网页中的实现
<!doctype html><html> <head> <meta charset="utf-8"/> <title> ...
- C# 6 元组应用 Part 1:方便的字典工厂方法
首先是简单的实现: public static class CollectionExtensions { public static IDictionary<TKey, TValue> M ...
- nginx的应用(window环境下)
nginx(背景) nginx是一个高性能的HTTP服务器,以前我经常在linux系统中配置,主要做反向代理和负载均衡,最近根据业务需要,需要在window中配置反向和负载,下面就介绍一下nginx的 ...
- (其他)SQL注入(转)
转自维基百科: SQL注入是一种代码注入技术,用于攻击数据驱动的应用程序,在这种应用程序中,恶意的SQL语句被插入输入字段中执行(例如将数据库内容转储给攻击者).[1] SQL注入必须利用应用程序软件 ...
- 逻辑回归&线性回归
# coding:utf-8 import numpy as np from sklearn import linear_model, datasets import matplotlib.pyplo ...
- ER模型试题
M公司为了便于开展和管理各项业务活动,提高公司的知名度和影响力,拟构建一个基于网络的会议策划系统. [需求分析结果] 该系统的部分功能及初步需求分析的结果如下 : (1)M公司旗下有业务部.策划部和其 ...
