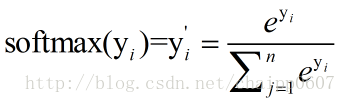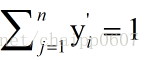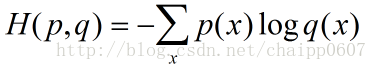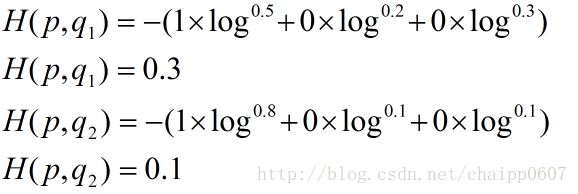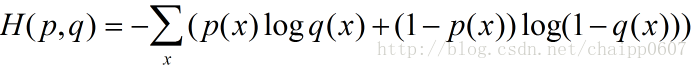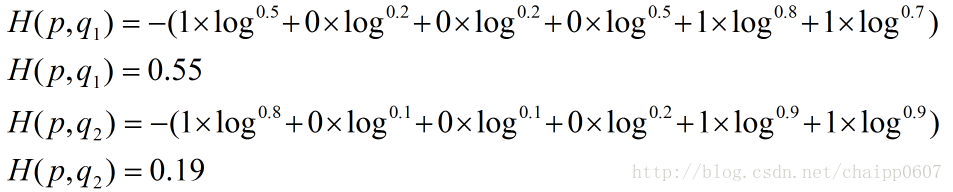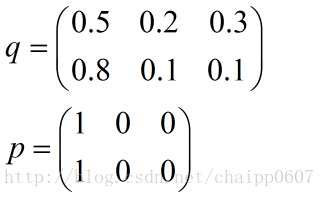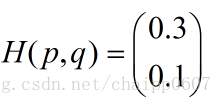理解交叉熵(cross_entropy)作为损失函数在神经网络中的作用
交叉熵的作用
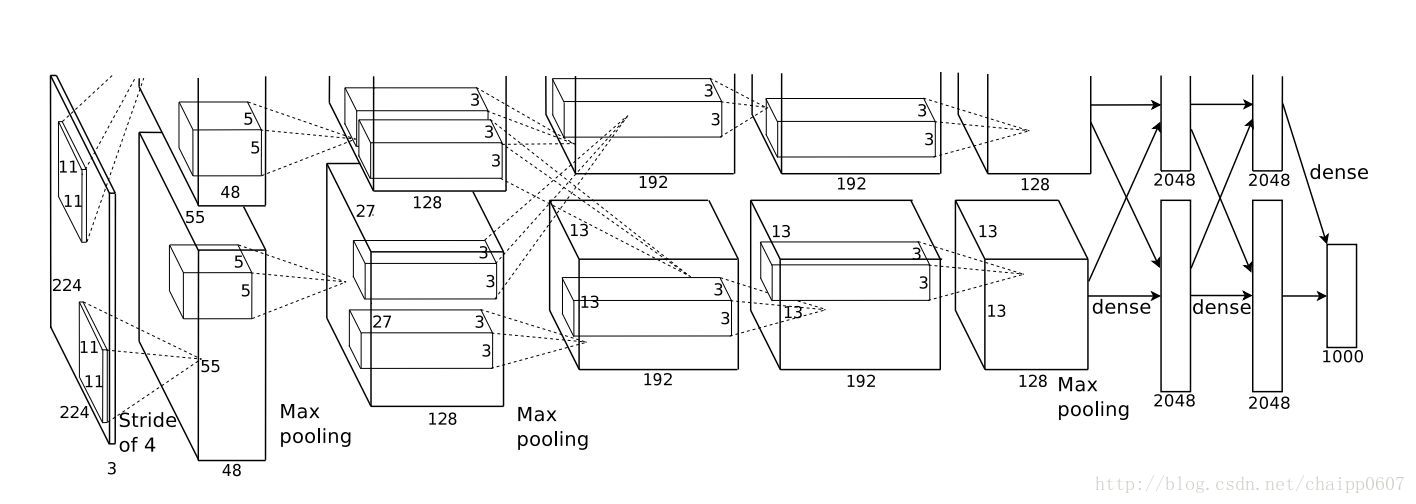
通过神经网络解决多分类问题时,最常用的一种方式就是在最后一层设置n个输出节点,无论在浅层神经网络还是在CNN中都是如此,比如,在AlexNet中最后的输出层有1000个节点:
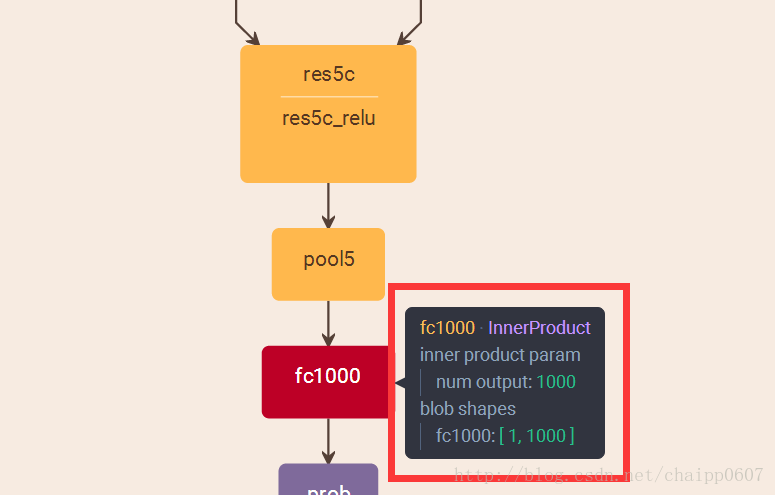
而即便是ResNet取消了全连接层,也会在最后有一个1000个节点的输出层:
一般情况下,最后一个输出层的节点个数与分类任务的目标数相等。假设最后的节点数为N,那么对于每一个样例,神经网络可以得到一个N维的数组作为输出结果,数组中每一个维度会对应一个类别。在最理想的情况下,如果一个样本属于k,那么这个类别所对应的的输出节点的输出值应该为1,而其他节点的输出都为0,即[0,0,1,0,….0,0],这个数组也就是样本的Label,是神经网络最期望的输出结果,交叉熵就是用来判定实际的输出与期望的输出的接近程度!
Softmax回归处理
神经网络的原始输出不是一个概率值,实质上只是输入的数值做了复杂的加权和与非线性处理之后的一个值而已,那么如何将这个输出变为概率分布?
这就是Softmax层的作用,假设神经网络的原始输出为y1,y2,….,yn,那么经过Softmax回归处理之后的输出为:
很显然的是:
而单个节点的输出变成的一个概率值,经过Softmax处理后结果作为神经网络最后的输出。
交叉熵的原理
交叉熵刻画的是实际输出(概率)与期望输出(概率)的距离,也就是交叉熵的值越小,两个概率分布就越接近。假设概率分布p为期望输出,概率分布q为实际输出,H(p,q)为交叉熵,则:
这个公式如何表征距离呢,举个例子:
假设N=3,期望输出为p=(1,0,0),实际输出q1=(0.5,0.2,0.3),q2=(0.8,0.1,0.1),那么:
很显然,q2与p更为接近,它的交叉熵也更小。
除此之外,交叉熵还有另一种表达形式,还是使用上面的假设条件:
其结果为:
以上的所有说明针对的都是单个样例的情况,而在实际的使用训练过程中,数据往往是组合成为一个batch来使用,所以对用的神经网络的输出应该是一个m*n的二维矩阵,其中m为batch的个数,n为分类数目,而对应的Label也是一个二维矩阵,还是拿上面的数据,组合成一个batch=2的矩阵:
所以交叉熵的结果应该是一个列向量(根据第一种方法):
而对于一个batch,最后取平均为0.2。
在TensorFlow中实现交叉熵
在TensorFlow可以采用这种形式:
cross_entropy = -tf.reduce_mean(y_ * tf.log(tf.clip_by_value(y, 1e-10, 1.0))) 其中y_表示期望的输出,y表示实际的输出(概率值),*为矩阵元素间相乘,而不是矩阵乘。
上述代码实现了第一种形式的交叉熵计算,需要说明的是,计算的过程其实和上面提到的公式有些区别,按照上面的步骤,平均交叉熵应该是先计算batch中每一个样本的交叉熵后取平均计算得到的,而利用tf.reduce_mean函数其实计算的是整个矩阵的平均值,这样做的结果会有差异,但是并不改变实际意义。
除了tf.reduce_mean函数,tf.clip_by_value函数是为了限制输出的大小,为了避免log0为负无穷的情况,将输出的值限定在(1e-10, 1.0)之间,其实1.0的限制是没有意义的,因为概率怎么会超过1呢。
由于在神经网络中,交叉熵常常与Sorfmax函数组合使用,所以TensorFlow对其进行了封装,即:
cross_entropy = tf.nn.softmax_cross_entropy_with_logits(y_ ,y)
与第一个代码的区别在于,这里的y用神经网络最后一层的原始输出就好了。
转:http://blog.csdn.net/chaipp0607/article/details/73392175
理解交叉熵(cross_entropy)作为损失函数在神经网络中的作用的更多相关文章
- 最大似然估计 (Maximum Likelihood Estimation), 交叉熵 (Cross Entropy) 与深度神经网络
最近在看深度学习的"花书" (也就是Ian Goodfellow那本了),第五章机器学习基础部分的解释很精华,对比PRML少了很多复杂的推理,比较适合闲暇的时候翻开看看.今天准备写 ...
- 深度学习基础系列(五)| 深入理解交叉熵函数及其在tensorflow和keras中的实现
在统计学中,损失函数是一种衡量损失和错误(这种损失与“错误地”估计有关,如费用或者设备的损失)程度的函数.假设某样本的实际输出为a,而预计的输出为y,则y与a之间存在偏差,深度学习的目的即是通过不断地 ...
- 【转载】深度学习中softmax交叉熵损失函数的理解
深度学习中softmax交叉熵损失函数的理解 2018-08-11 23:49:43 lilong117194 阅读数 5198更多 分类专栏: Deep learning 版权声明:本文为博主原 ...
- softmax交叉熵损失函数求导
来源:https://www.jianshu.com/p/c02a1fbffad6 简单易懂的softmax交叉熵损失函数求导 来写一个softmax求导的推导过程,不仅可以给自己理清思路,还可以造福 ...
- 交叉熵理解:softmax_cross_entropy,binary_cross_entropy,sigmoid_cross_entropy简介
cross entropy 交叉熵的概念网上一大堆了,具体问度娘,这里主要介绍深度学习中,使用交叉熵作为类别分类. 1.二元交叉熵 binary_cross_entropy 我们通常见的交叉熵是二元交 ...
- TensorFlow笔记-06-神经网络优化-损失函数,自定义损失函数,交叉熵
TensorFlow笔记-06-神经网络优化-损失函数,自定义损失函数,交叉熵 神经元模型:用数学公式比表示为:f(Σi xi*wi + b), f为激活函数 神经网络 是以神经元为基本单位构成的 激 ...
- 【机器学习基础】交叉熵(cross entropy)损失函数是凸函数吗?
之所以会有这个问题,是因为在学习 logistic regression 时,<统计机器学习>一书说它的负对数似然函数是凸函数,而 logistic regression 的负对数似然函数 ...
- 深度学习中交叉熵和KL散度和最大似然估计之间的关系
机器学习的面试题中经常会被问到交叉熵(cross entropy)和最大似然估计(MLE)或者KL散度有什么关系,查了一些资料发现优化这3个东西其实是等价的. 熵和交叉熵 提到交叉熵就需要了解下信息论 ...
- 交叉熵代价函数——当我们用sigmoid函数作为神经元的激活函数时,最好使用交叉熵代价函数来替代方差代价函数,以避免训练过程太慢
交叉熵代价函数 machine learning算法中用得很多的交叉熵代价函数. 1.从方差代价函数说起 代价函数经常用方差代价函数(即采用均方误差MSE),比如对于一个神经元(单输入单输出,sigm ...
随机推荐
- HDU 3594.Cactus 仙人掌图
Cactus Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)Total Subm ...
- Netty学习路线总结
序 之前开过品味性能系列.Mysql学习系列,颇为曲高和寡.都是讲理论,很少有手把手深入浅出的文章.不过确实我就这脾气,文雅点的说法叫做"伪雅",下里巴人叫做"装逼&qu ...
- MyAdvice 填充方法(在原有方法上添加方法)
//applicationContext.xml配置文件 /UserServiceImp继承于UserService接口 <!-- 1 配置目标对象--> <bean nam ...
- 家庭家长本-微信小程序
寒假在家的时候,做了一个简单的网页版家庭账本,后来自己学习了微信小程序的制作方法,现在想做一个微信小程序的家庭记账本. 首先要在微信公众平台注册一个微信小程序的账号,用的邮箱一个只能注册一个微信小程序 ...
- 转载-对js中new、prototype的理解
说明:本篇文章是搜集了数家之言,综合的结果,应向数家致谢 说到prototype,就不得不先说下new的过程. 我们先看看这样一段代码: <script type="text/java ...
- MFC禁用关闭按钮
有时候我们在写MFC程序时,需要在对话框中开启线程处理一些事情,如果在线程执行过程中点击关闭按钮,会导致程序崩溃. 这里介绍一种解决方法,禁用关闭按钮 解决方法 开启线程前禁用关闭按钮 CMenu* ...
- 【转】Map 与 Unordered_map
map和unordered_map的差别和使用 map和unordered_map的差别还不知道或者搞不清unordered_map和map是什么的,请见:http://blog.csdn.net/b ...
- unigui 调用js
//引用单元uniguiapplicationUniSession.AddJS('alert(unigui调用了JS方法)');
- 记web模拟手机环境已经微信开发者工具中可正常运行,实体机运行报错问题
问题描述: 有个手机微信OA的项目 用户信息采用cookie方式保存.发布后使用chorme浏览器进行模拟访问测试发现一切运行顺畅,使用微信开发者工具进行测试也一切正常. 采用实体机进行测试时,用微信 ...
- maya2012卸载/安装失败/如何彻底卸载清除干净maya2012注册表和文件的方法
maya2012提示安装未完成,某些产品无法安装该怎样解决呢?一些朋友在win7或者win10系统下安装maya2012失败提示maya2012安装未完成,某些产品无法安装,也有时候想重新安装maya ...