Deep Learning.ai学习笔记_第二门课_改善深层神经网络：超参数调试、正则化以及优化

目录

第一周（深度学习的实践层面）

第二周（优化算法）

第三周（超参数调试、Batch正则化和程序框架）

目标： 如何有效运作神经网络，内容涉及超参数调优，如何构建数据，以及如何确保优化算法快速运行，从而使学习算法在合理时间内完成自我学习。

第一周（深度学习的实践层面）

如何选取一个神经网络的训练集、验证集和测试集呢？

如果数据量比较少，例如只有100条，1000条或者1万条数据，按照60%、20%、20%划分是比较合理的，但是在目前大部分数据都是远远大于这个数理级，也可以说是大数据规模的级别。那么，此时选择的比例比较合适的为训练集占98%，验证集和测试集各占1%。

在对于验证集和测试集的数据选择上，尽量确保这两部分数据来自同一分布，这样处理的是会使得算法的性能验证结果更加精确。

优化神经网络性能的基本思路

合理地分析训练集在训练算法产生的误差和验证集上验证算法产生的误差来诊断算法是否存在高偏差和高方差，对系统地优化算法有很大的帮助。

在训练神经网络时，如果算法的偏差很高，甚至无法拟合训练集，那么此时需要选择一个新的网络，比如含有更多隐藏层或者隐藏单元的网络，或者花费更多时间来训练网络，或者尝试更先进的优化算法。

训练网络完成后，验证其性能时，如果方差很高，最好的解决办法就是采用更多数据，如果能够做到，会有一定的帮助，但有时候，我们无法获得更多数据，我们也可以尝试通过正则化来减少过拟合。

L2正则化方法

L2正则化更新W值过程

为什么正则化有利于预防过拟合呢？

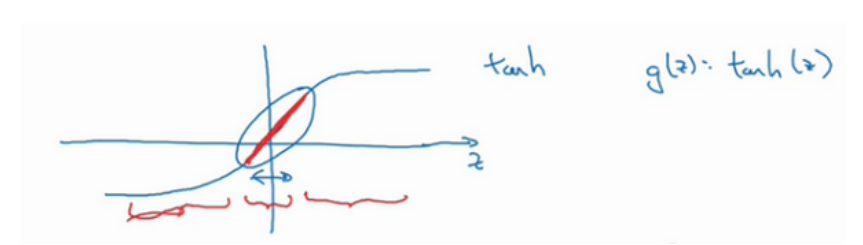
如果正则化参数很大，激活函数的参会会相对较小，因为代价函数的参数变大了。如果W很小，相对来说，z也会很小。此时，激活函数g(z)大致呈线性，和线性回归函数一样，此时就可以很好地解决过拟合问题。具体如下图：

dropout正则化

使用数据扩增可以有效减少神经网络中的过拟合，例如把已有数据进行相关处理，可以把图片翻转或者变形压缩等处理，这样就大大增加了已有样本数据集的数量。

此外，还可以选择采用early stopping方式来减少神经网络中的过拟合。例如下图:

梯度检验应用的注意事项

首先，不要在训练中使用梯度检验，它只用于调试。

第二点，如果算法的梯度检验失败，要检查所有项，检查每一项，并试着找出bug。

第三点，在实施梯度检验时，如果使用正则化，请注意正则项。

第四点，梯度检验不能与dropout同时使用，因为每次迭代过程中，dropout会随机消除隐藏层单元的不同子集，难以计算dropout在梯度下降上的代价函数J。

最后一点，也是比较微妙的一点，现实中几乎不会出现这种情况。当w和b接近0时，梯度下降的实施是正确的，在随机初始化过程中……，但是在运行梯度下降时，w和b变得更大。可能只有在w和b接近0时，backprop的实施才是正确的。但是当W和b变大时，它会变得越来越不准确。你需要做一件事，我（吴恩达老师）不经常这么做，就是在随机初始化过程中，运行梯度检验，然后再训练网络，w和b会有一段时间远离0，如果随机初始化值比较小，反复训练网络之后，再重新运行梯度检验。

第二周（优化算法）

Mini-batch梯度下降简单介绍

mini-bach梯度下降法，核心是把输入数据以及输出数据，以一定数量组分组变成向量化的结果进行相关计算，这样做的好处就是循环次数大大减少，也能够提高运行效率。下图可参考：

使用batch（批量）梯度下降法，一次遍历训练集只能让你做一个梯度下降，使用mini-batch梯度下降法，一次遍历训练集，能让你做5000个梯度下降。当然正常来说你想要多次遍历训练集，还需要为另一个while循环设置另一个for循环。所以你可以一直处理遍历训练集，直到最后你能收敛到一个合适的精度。

如果你有一个丢失的训练集，mini-batch梯度下降法比batch梯度下降法运行地更快，所以几乎每个研习深度学习的人在训练巨大的数据集时都会用到。

mini-bathc梯度下降法和batch梯度下降法随着训练次数的关系图：

如果mini-batch中设置的分组数目大小为1，此时算法就变成了随机梯度下降法。

样本集较小时，推荐直接使用batch梯度下降法，此时没有必要使用mini-batch梯度下降法。

使用mini-batch梯度下降法注意点

在使用mini-batch梯度下降法时要注意选定的分组数目要合理，一般选择2的指数次，例如64或者512。如果选择的数目不合理，会因为你训练所在的CPU/GPU内存不相符，导致算法的表现得不到预期效果。

理解指数加权平均数

指数加权平均数，类似一个等比数列和等差数列的组合体，计算第n项需要不断迭代，如下图：

动量梯度下降法

加快学习算法的一个办法就是随时间慢慢减少学习率，我们将之称为学习率衰减。

梯度下降

在机器学习中，最简单就是没有任何优化的梯度下降(GD,Gradient Descent)，我们每一次循环都是对整个训练集进行学习，这叫做批量梯度下降(Batch Gradient Descent)，我们之前说过了最核心的参数更新的公式，这里我们再来看一下：

由梯度下降算法演变来的还有随机梯度下降（SGD）算法和小批量梯度下降算法，随机梯度下降（SGD），相当于小批量梯度下降，但是和mini-batch不同的是其中每个小批量(mini-batch)仅有1个样本，和梯度下降不同的是你一次只能在一个训练样本上计算梯度，而不是在整个训练集上计算梯度。

包含动量的梯度下降

Adam算法

Adam的一些优点包括相对较低的内存要求（虽然比梯度下降和动量下降更高）和通常运作良好，即使对参数进行微调（除了学习率α）。

第三周（超参数调试、Batch正则化和程序框架）

调试处理

在训练神经网络时，有很多参数需要调整来使得训练结果变得更加合理，其中经常需要调试的参数为学习速率a。

当有多个超参数需要调节时，可以采用由粗糙到精细的策略，即估算出最佳参数的调节范围，然后再在缩小的调节范围中精细调节。

超参数调试的实践

（1） 你照看一个模型，通常是有庞大的数据组，但没有许多计算资源或足够的CPU和GPU的前提下，基本而言，你只可以一次负担起试验一个模型或一小批模型，在这种情况下，即使当它在试验时，你也可以逐渐改良。类比哺乳动物照看孩子，例如熊猫，一般只能照看一个孩子

（2） 同时试验多种模型，你设置了一些超参数，尽管让它自己运行，或者是一天甚至多天，然后你会获得不同的学习曲线，这可以是损失函数J或实验误差或损失或数据误差的损失，但都是你曲线轨迹的度量。类比鱼产卵，可以由很多很多，但其中只要有成功存活就可以。

Batch归一化一次只能处理一个mini-batch数据，它在mini-batch上计算均值和方差。 使用Batch归一化，能够训练更深的网络，让学习算法运行速度更快。

Softmax回归

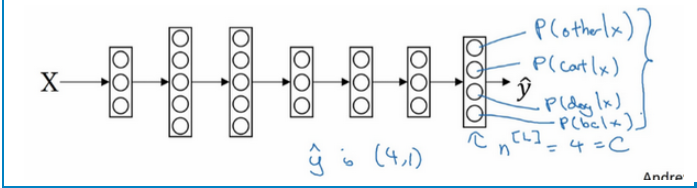
有一种logistic回归的一般形式，叫做Softmax回归，能让你在试图识别某一分类时做出预测，或者说是多种分类中的一个，不只是识别两个分类。 Softmax回归或Softmax激活函数将logistic激活函数推广到C类，而不仅仅是两类。可以参考下图的输出层：

Tesorflow框架使用

初始化Tensorflow变量后，进行相关运算时，例如乘法运算，运算前需要创建一个session，然后调用session.run()方法才能成功完成相关运算。

参考资料：

1.https://blog.csdn.net/u013733326/article/details/79907419

2.http://www.ai-start.com/