C++之易混淆知识点三---算法分析

最近复习算法，感到有一丝丝忘记的困惑，赶紧记下来。。。

一、分治法

分治法的思想就是“分而治之”，很明显就是将规模比较庞大、复杂的问题进行分治，然后得到多个小模块，最好这些小模块之间是独立的，如果这些小模块之间耦合性比较大的话，需要多次计算重复的问题，从而出现了冗余，这种情况下，可以利用动态规划法，保存这些小模块问题的解，这样就避免了多次重复计算相同问题的解了。分治法的一般解题步骤包括：

根据分治法的解题思想，我们可以看到这其中需要用到递归。以斐波那契函数为例：

现在要求计算，则使用分治法解题时，得到下面的过程。

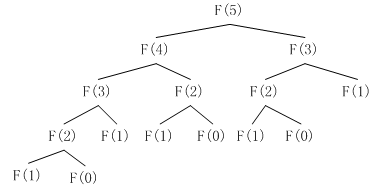
例如：使用分治法求解最大子段和问题。如下图所示：

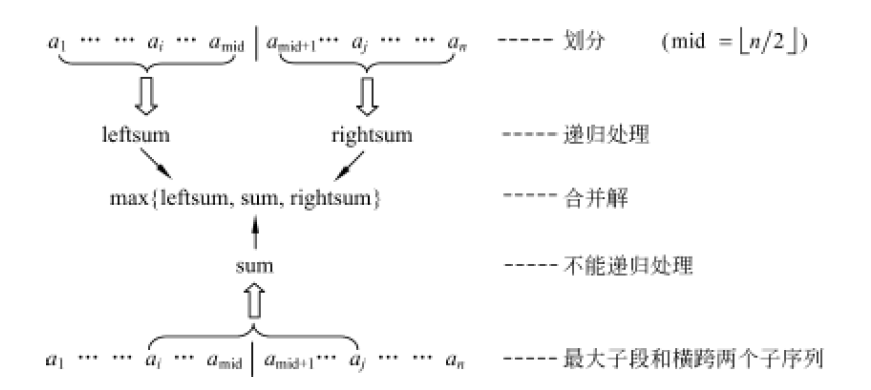
//分治法求解
int DivideCom(int a[],int left,int right)
{
    int maxsum=;
    if (left==right)   //直接求解
    {
        if (a[left]>)
        {
            maxsum=a[left];
        }
        else maxsum=;
    }
    else
    {
        int mid=(left+right)/;
        int leftsum=DivideCom(a,left,mid);
        int rightsum=DivideCom(a,mid+,right);
 
        int lefts=,rights=,temp=;
        for (int i=mid;i>=left;--i)
        {
            temp+=a[i];
            if (temp>lefts)
            {
                lefts=temp;
            }
        }
        for (i=mid+;i<=right;++i)
        {
            temp+=a[i];
            if (temp>rights)
            {
                rights=temp;
            }
        }
        maxsum=lefts+rights;
        if (leftsum>maxsum)
        {
            maxsum=leftsum;
        }
        if (rightsum>maxsum)
        {
            maxsum=rightsum;
        }
    }
 
    return maxsum;
}

二、动态规划法

动态规划法最初就解决数学最优化问题的工具，现在计算机领域中多用来解决多阶段决策问题。动态规划法解题的时候也是对原来大问题进行划分，得到多个可以相互重叠的子问题，对应于问题求解过程中的多个决策阶段，然后计算每个阶段的解，并保存下来，在后面遇到需要重复计算的问题时可以查表直接使用前面已经计算过的值，这一点有别于分治法。以上述的斐波那契函数为例，在使用动态规划求解的时候，不是重复求解系那个天表达式值，而是将每一次求解的值存入一个表格中，如下表：

n	0	1	2	3	4	5	6	7
F(n)	0	1	1	2	3	5	8	13

动态规划的一般解题步骤包括：

例如：使用动态规划法求解最大子段和问题。假设对序列A={a1,a2,a3,......,an}求解最大子段和，则求解的动态规划函数为：

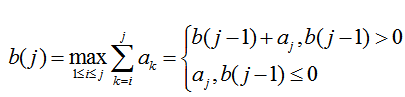
//动态规划法
int DynamicP(int a[],int n)
{
    int maxsum=;
    int *b=(int*)malloc(n*sizeof(int));
 
    maxsum=b[]=a[];
    for (int i=;i<n;i++)
    {
        if (b[i-]>)
        {
            b[i]=b[i-]+a[i];
        }
        else
            b[i]=a[i];
 
        if (maxsum<b[i])
        {
            maxsum=b[i];
        }
    }
 
    delete[] b;
    return maxsum;
}

三、贪心法

贪心算法也是对所求的问题进行分解，得到多个较为简单的局部最优选择，通过求解每一步局部最优选择的解，最后得到问题的最终解。贪心法在求解局部最优解时，只根据当前的判断进行选择，不管将来的结果，即属于局部最优选择，所以贪心法得到的结果不一定是整体最优解，但却是获得近似最优解的好方法，而动态规划中，每一步所做出的选择或者决策往往依赖于相关子问题的解，只有在求得相关子问题的解以后，才能做出选择。还有一点：动态规划是自底向上求解问题的解，而贪心法是自顶向下求解。

贪心法的一般求解过程如下：
Greedy(C)   //C是问题的输入集合，即候选集合
{
   S={}； //S是解集合，初始解集合为空
   while(not solution(S))  //集合S没有构成问题的解
{
   X=select(S);  //在候选集合C中进行贪心选择，即选择局部最优
   if feasible(S,X)  //判断解集合中加入X是否可行
   {
      S=S+{X}；
}
C=C-{X}；
}
}