POJ 3150 Cellular Automaton(矩阵高速幂)

题目大意：给定n（1<=n<=500）个数字和一个数字m，这n个数字组成一个环(a0,a1.....an-1)。假设对ai进行一次d-step操作，那么ai的值变为与ai的距离小于d的全部数字之和模m。求对此环进行K次d-step（K<=10000000）后这个环的数字会变为多少。

看了一篇博客：http://www.cppblog.com/varg-vikernes/archive/2011/02/08/139804.html说的非常清楚。

拿例子来说：

a矩阵：

a = 1 2 2 1 2

构造出来一个矩阵：

b = 

1 1 0 0 1

1 1 1 0 0

0 1 1 1 0

0 0 1 1 1

1 0 0 1 1

(a4+a0+a1) (a0+a1+a2) (a1+a2+a3) (a2+a3+a4) (a3+a4+a0)得到的矩阵e = 5 5 5 5 4

所以题意就是：a*(b^k) = e。求出e就是通过解b^k。由于直接求b^k会超时，所以要二分求幂。

这个题的矩阵另一个性质：

利用矩阵A。B具有A[i][j]=A[i-1][j-1],B[i][j]=B[i-1][j-1]（i-1<0则表示i-1+n,j-1<0则表示j-1+n）

我们能够得出矩阵C=a*b也具有这个性质

C[i][j]=sum(A[i][t]*B[t][j])=sum(A[i-1][t-1],B[t-1][j-1])=sum(A[i-1][t],B[t][j-1])=C[i-1][j-1] 

“”“

所以能够求出C[0][0],以后的递推得到。

Cellular Automaton

Time Limit: 12000MS		Memory Limit: 65536K
Total Submissions: 3057		Accepted: 1232
Case Time Limit: 2000MS

Description

A cellular automaton is a collection of cells on a grid of specified shape that evolves through a number of discrete time steps according to a set of rules that describe the new state of a cell based on the states of neighboring cells. The order
of the cellular automaton is the number of cells it contains. Cells of the automaton of order n are numbered from 1 to n.

The order of the cell is the number of different values it may contain. Usually, values of a cell of order m are considered to be integer numbers from 0 to m − 1.

One of the most fundamental properties of a cellular automaton is the type of grid on which it is computed. In this problem we examine the special kind of cellular automaton — circular cellular automaton of order n with cells of order m.
We will denote such kind of cellular automaton as n,m-automaton.

A distance between cells i and j in n,m-automaton is defined as min(|i − j|, n − |i − j|). A d-environment of a cell is the set of cells at a distance not greater than d.

On each d-step values of all cells are simultaneously replaced by new values. The new value of cell i after d-step is computed as a sum of values of cells belonging to the d-enviroment of the cell i modulo m.

The following picture shows 1-step of the 5,3-automaton.

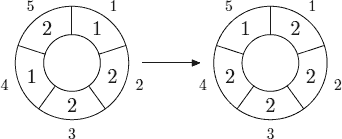
The problem is to calculate the state of the n,m-automaton after k d-steps.

Input

The first line of the input file contains four integer numbers n, m, d, and k (1 ≤ n ≤ 500, 1 ≤ m ≤ 1 000 000, 0 ≤ d < ⁿ⁄₂ , 1 ≤ k ≤ 10 000 000). The second
line contains n integer numbers from 0 to m − 1 — initial values of the automaton’s cells.

Output

Output the values of the n,m-automaton’s cells after k d-steps.

Sample Input

sample input #1
5 3 1 1
1 2 2 1 2

sample input #2
5 3 1 10
1 2 2 1 2

Sample Output

sample output #1
2 2 2 2 1

sample output #2
2 0 0 2 2

#include <algorithm>
#include <iostream>
#include <stdlib.h>
#include <string.h>
#include <iomanip>
#include <stdio.h>
#include <string>
#include <queue>
#include <cmath>
#include <stack>
#include <map>
#include <set>
#define eps 1e-10
#define LL __int64
///#define LL long long
///#define INF 0x7ffffff
#define INF 0x3f3f3f3f
#define PI 3.1415926535898
#define zero(x) ((fabs(x)<eps)?

0:x)

const int maxn = 550;

using namespace std;

LL e[maxn][maxn];
LL c[maxn][maxn];
LL xmul[maxn][maxn];
LL num[maxn];
LL ans[maxn];
int n, m, d;

void Mul(LL a[][maxn], LL b[][maxn])
{
    memset(c, 0, sizeof(c));
    for(int i = 0; i < n; i++)
    {
        if(!a[0][i])
            continue;
        for(int j = 0; j < n; j++)
        {
            c[0][j] += a[0][i]*b[i][j];
            c[0][j] %= m;
        }
    }
    for(int i = 1; i < n; i++)
        for(int j = 0; j < n; j++) c[i][j] = c[i-1][(j-1+n)%n];
    for(int i = 0; i < n; i++)
        for(int j = 0; j < n; j++) b[i][j] = c[i][j];
}

void expo(LL a[][maxn], int k)
{
    if(k == 1)
    {
        for(int i = 0; i < n; i++)
            for(int j = 0; j < n; j++) e[i][j] = a[i][j];
        return;
    }
    memset(e, 0, sizeof(e));
    for(int i = 0; i < n; i++) e[i][i] = 1;
    while(k)
    {
        if(k&1) Mul(a, e);
        Mul(a, a);
        k /= 2;
    }
}
int main()
{
    int k;
    while(cin >>n>>m>>d>>k)
    {
        for(int i = 0; i < n; i++) cin >>num[i];
        memset(xmul, 0, sizeof(xmul));
        xmul[0][0] = 1;
        for(int i = 1; i <= d; i++) xmul[0][i] = xmul[0][n-i] = 1;
        for(int i = 1; i < n; i++)
            for(int j = 0; j < n; j++) xmul[i][j] = xmul[i-1][(j-1+n)%n];
        expo(xmul, k);
        memset(ans, 0, sizeof(ans));
        for(int i = 0; i < n; i++)
        {
            for(int j = 0; j < n; j++)
            {
                ans[i] += e[i][j]*num[j];
                ans[i] %= m;
            }
        }
        for(int i = 0; i < n-1; i++) cout<<ans[i]<<" ";
        cout<<ans[n-1]<<endl;
    }
    return 0;
}