TRS矩阵分解

transform = TRS

T就是transform的最后一列。关于R和S的分解，PBRT给了一个公式：M_(i+1) = (M_i + ((M_i)^T)^(-1))*0.5，直到M收敛。M初始状态为transform左上角的3*3的矩阵。

M收敛后得到的矩阵为R，从而可以解出S.代码大概是这样：

        void decompose(Vec3<float>& T, Mat33<float> &R, Vec3<float>& S) {
            T[] = m[][], T[] = m[][], T[] = m[][];
 
            Mat33<float> M0 = *this;
            while (true) {
                auto M1 = (M0 + M0.transpose().inverse()) * 0.5;
                if (M0.equals(M1)) break;
                M0 = M1;
            }
 
            R = M0;
 
            _RUNTIME_ASSERT_((M0*M0.transpose()).equals(Mat33<float>::eye()), "(M0*M0.transpose()).equals(eye())");
 
            auto SM = R.transpose() * Mat33<float>(*this);
            S[] = SM[][], S[] = SM[][], S[] = SM[][];
        }

还有一种方法?：简单验证了下，如果transform 是由TRS得到的，二者恢复出来的是一样的，但TSR就不一样了？

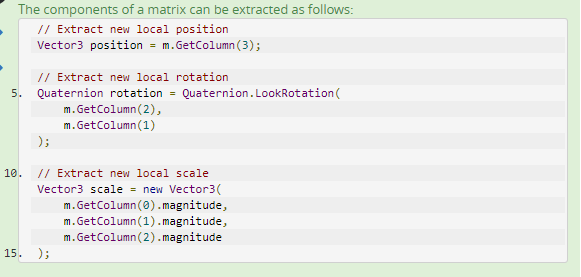
S是前三列的magnitude。R根据第三列forward，第二列upward恢复。

https://answers.unity.com/questions/402280/how-to-decompose-a-trs-matrix.html