POJ2976 Dropping tests(01分数规划）

题意

给你n次测试的得分情况b[i]代表第i次测试的总分,a[i]代表实际得分。

你可以取消k次测试，得剩下的测试中的分数为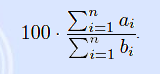

问分数的最大值为多少。

题解

裸的01规划。

然后ans没有清0坑我半天。

 #include<iostream>
 #include<cstring>
 #include<cmath>
 #include<cstdio>
 #include<algorithm>
 using namespace std;
 const int N=;
 double a[N],b[N],c[N],ans;
 int n,k;
 bool judge(double x){
     double tmp=;
     for(int i=;i<=n;i++){
         c[i]=a[i]-x*b[i];
     }
     sort(c+,c++n);
     for(int i=k+;i<=n;i++){
         tmp+=c[i];
     }
     if(tmp>=)return true;
     else return false;
 }
 int main(){
     scanf("%d%d",&n,&k);
     while(n!=||k!=){
         for(int i=;i<=n;i++){
             scanf("%lf",&a[i]);
         }
         for(int i=;i<=n;i++){
             scanf("%lf",&b[i]);
         }
         double l=0.00;double r=1.00;
         ans=;
         while(1e-<=r-l){
             double mid=(l+r)/;
             if(judge(mid)){
                 ans=mid;
                 l=mid+1e-;
             }
             else r=mid-1e-;
         }
         printf("%0.lf\n",ans*);
         scanf("%d%d",&n,&k);
     }
 }