SHOI2013 扇形面积并

题目链接：戳我

补一张图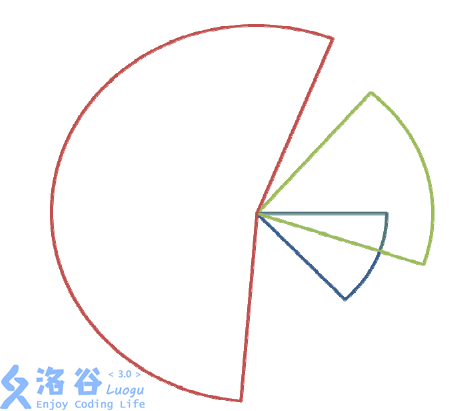

我们尝试把圆上的扇形转化成直线上的矩形——我们维护[1,2m]的区间，那么每个能产生贡献的子区间的长度第K大的半径的平方的总和就是answer了。

怎么转化呢？左端点为a1+m+1，右端点为a2+m。为什么要+m？因为原先的范围是[-m,m]的，所以整体右移。为什么左端点要+1？因为我们维护的是区间，所以这里的每一个下标表示的是以该position为右端点，长度为1的区间。

我们先按照半径长度从大到小排序，如果一个区间覆盖数量超过K个，就不需要再处理了。（优化时间复杂度）

之后就是线段树操作了。我们在更改的同时求出答案。（其实分开写也行，就是要注意因为我们乘上的系数使然，所以区间必须也是当前的修改区间）

minn表示该区间的所有子区间覆盖量的min，maxx是该区间的所有子区间的覆盖量的max。

注意我们的siz是由左右子区间合并而来的。所以产生贡献之后，记得赋值为0，这样就不会对它的父亲区间产生贡献了。

代码如下：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#define MAXN 2000010
using namespace std;
int n,m,k;
long long ans=0;
struct Node{int l,r,c;}node[MAXN];
struct Node2{int l,r,tag,minn,maxx,siz;}t[MAXN<<2];
inline bool cmp(struct Node x,struct Node y){return x.c>y.c;}
inline int ls(int x){return x<<1;}
inline int rs(int x){return x<<1|1;}
inline void push_up(int x)
{
    t[x].maxx=max(t[ls(x)].maxx,t[rs(x)].maxx);
    t[x].minn=min(t[ls(x)].minn,t[rs(x)].minn);
    t[x].siz=t[ls(x)].siz+t[rs(x)].siz;
}
inline void build(int x,int l,int r)
{
    t[x].l=l,t[x].r=r;
    if(l==r) {t[x].siz=1;return;}
    int mid=(l+r)>>1;
    build(ls(x),l,mid);
    build(rs(x),mid+1,r);
    push_up(x);
}
inline void solve(int x,int k)
{
    t[x].tag+=k;
    t[x].minn+=k;
    t[x].maxx+=k;
}
inline void push_down(int x)
{
    int l=t[x].l,r=t[x].r;
    if(t[x].tag)
    {
        solve(ls(x),t[x].tag);
        solve(rs(x),t[x].tag);
        t[x].tag=0;
    }
}
inline int update_query(int x,int ll,int rr)
{
    int l=t[x].l,r=t[x].r;
    if(t[x].minn>=k) return 0;
    if(ll<=l&&r<=rr)
    {
        if(t[x].maxx<k-1) {t[x].minn++,t[x].maxx++,t[x].tag++;return 0;}
        if(t[x].minn>=k-1)
        {
            int cur_ans=t[x].siz;
            t[x].siz=0;
            t[x].minn++;
            return cur_ans;
        }
        int cur_ans=0;
        push_down(x);
        cur_ans+=update_query(ls(x),ll,rr);
        cur_ans+=update_query(rs(x),ll,rr);
        push_up(x);
        return cur_ans;
    }
    push_down(x);
    int mid=(l+r)>>1;
    int cur_ans=0;
    if(ll<=mid) cur_ans+=update_query(ls(x),ll,rr);
    if(mid<rr) cur_ans+=update_query(rs(x),ll,rr);
    push_up(x);
    return cur_ans;
}
int main()
{
    #ifndef ONLINE_JUDGE
    freopen("ce.in","r",stdin);
    #endif
    scanf("%d%d%d",&n,&m,&k);
    for(int i=1;i<=n;i++)
    {
        scanf("%d%d%d",&node[i].c,&node[i].l,&node[i].r);
        node[i].l+=m+1;
        node[i].r+=m;
    }
    sort(&node[1],&node[n+1],cmp);
    build(1,1,m*2);
    for(int i=1;i<=n;i++)
    {
        int cur_ans=0;
        if(node[i].l<node[i].r)
            cur_ans+=update_query(1,node[i].l,node[i].r);
        else if(node[i].l>node[i].r)
        {
            cur_ans+=update_query(1,node[i].l,m*2);
            cur_ans+=update_query(1,1,node[i].r);
        }
        ans+=1ll*cur_ans*node[i].c*node[i].c;
        //printf("i=%d ans=%lld\n",i,ans);
    }
    printf("%lld\n",ans);
    return 0;
}