587. Erect the Fence（凸包算法）

问题

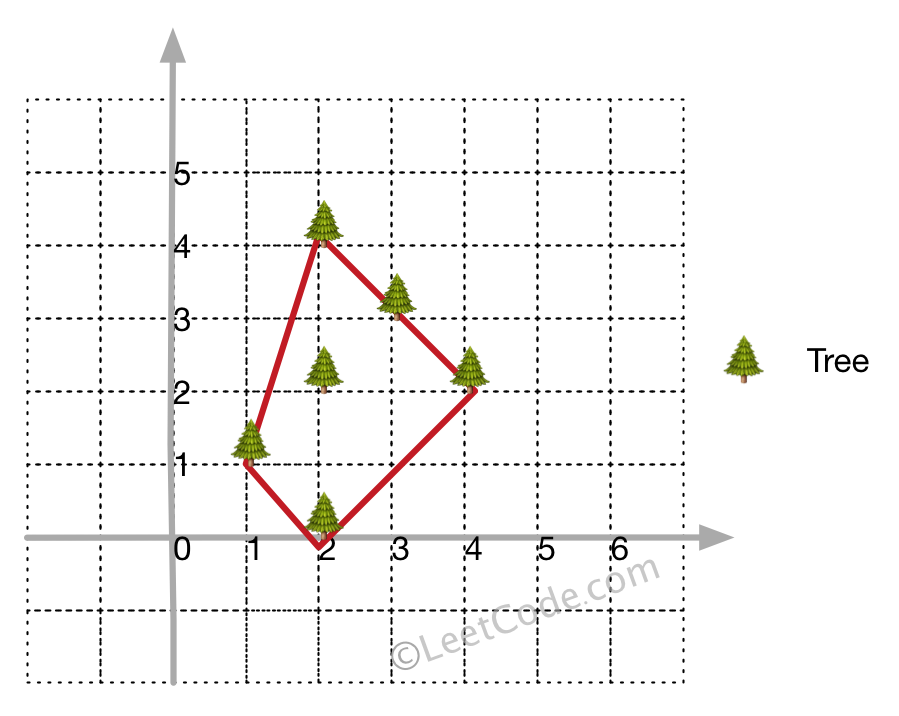
给定一群树的坐标点，画个围栏把所有树围起来（凸包）。

至少有一棵树，输入和输出没有顺序。

Input: [[1,1],[2,2],[2,0],[2,4],[3,3],[4,2]]

Output: [[1,1],[2,0],[4,2],[3,3],[2,4]]

思路和代码

1. 暴力法（超时）

对于任意两点连成的一条直线，如果其它所有点都在这条直线的一侧，则这两个点为解集中的两个点。

怎么判断点在直线的同一侧呢？

假设确定直线的两点为p1(x1, y1)和p2(x2, y2)，方向从p1到p2，两点代入直线方程Ax+By+C=0，得到

A = y2 - y1;

B = x1 - x2;

C = x2 * y1 - x1 * y2.

将其它所有点p代入直线方程Ax + By + C，大于0说明在直线右侧，小于0说明在直线左侧，等于0说明在直线上。

时间复杂度O(n^3)，空间复杂度O(n)

# Definition for a point.
# class Point(object):
#    def __init__(self, a=0, b=0):
#        self.x = a
#        self.y = b

class Solution(object):
    def outerTrees(self, points):
        """
        :type points: List[Point]
        :rtype: List[Point]
        """
        n = len(points)
        if n < 4:
            return points
        convex_index = [0] * n
        for i in range(n):
            for j in range(i + 1, n):
                x1, y1 = points[i].x, points[i].y
                x2, y2 = points[j].x, points[j].y
                first = same_direct = True
                first_direct = 0
                for k in range(n):
                    if (k != i and k != j):
                        x3, y3 = points[k].x, points[k].y
                        direct = (y2 - y1) * x3 + (x1 - x2) * y3 + x2 * y1 - x1 * y2
                        if first and direct != 0:
                            first_direct = direct
                            first = False
                        if first == False and first_direct * direct < 0:
                            same_direct = False
                            break
                if (same_direct):
                    convex_index[i] = convex_index[j] = 1
        return [points[i] for i in range(n) if convex_index[i]]

2. 分治法

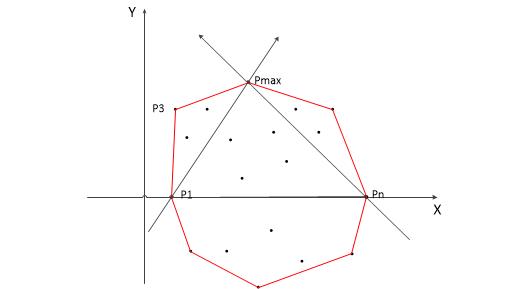
（1）横坐标最小和最大的点一定在解集中，记为P1和P2，直线P1P2把所有点分成了两部分，上包和下包。如下图所示（图源见参考资料）

（2）对上包，求距离直线P1P2最远的点，记为Pmax。

（3）点到直线的距离公式为(Ax+By+C) / 根号(A^2+B2)，如果是比较大小的话可以忽略分母直接计算分子，同时考虑直线方向是从左往后，Pmax在直线的左侧，距离求出来是负的，需要取一个负号。

（4）连接P1Pmax直线，以左侧为上包，执行上述操作

（5）连接PmaxP2直线，也以左侧为上包，执行上述操作。

（6）对下包也执行类似的操作。

时间复杂度O(N*logN)，空间复杂度O(N)

class Solution(object):
    def outerTrees(self, points):
        """
        :type points: List[Point]
        :rtype: List[Point]
        """
        n = len(points)
        if n < 4:
            return points
        self.convex_index = [0] * n
        points = sorted(points, key = lambda p: (p.x, p.y))
        self.convex_index[0] = 1
        self.convex_index[n-1] = 1

        self.div(points, 0, n-1)
        self.div(points, n-1, 0)

        return [points[i] for i in range(n) if self.convex_index[i]]

    def div(self, points, left, right):
        if(left < right and right - left <= 1 or left > right and left - right <= 1):
            return
        x1, y1 = points[left].x, points[left].y
        x2, y2 = points[right].x, points[right].y
        max_distance = 0
        max_index = -1
        i = min(left, right)
        i += 1
        while True:
            x3, y3 = points[i].x, points[i].y
            distance = - ((y2 - y1) * x3 + (x1 - x2) * y3 + x2 * y1 - x1 * y2)
            if distance >= max_distance:
                max_distance = distance
                max_index = i
            i += 1
            if( left < right and i == right or right < left and i == left):
                break

        if max_index != -1:
            self.convex_index[max_index] = 1
            self.div(points, left, max_index)
            self.div(points, max_index, right)

3. Jarvis算法

（1）横坐标最小的点一定是凸包上的点，记为p，从p开始按逆时针方向找点，每次找最靠近外侧的点。

（2）先假设数组中的下一个点为点q，然后遍历剩余的点r，如果存在点r位于向量pq的右侧，则更新q（q=r），这样遍历完后就可以找到q。在暴力法中我们用直线方程的公式来判断点所处的位置，其实可以使用叉积的方式（相关解释见第5点），如果pq x qr的模小于0，说明pq转向qr（0到180度以内）是顺时针，r位于pq的右侧，此时把q更新为r（q = r）。

（3）然后更新p（p = q），继续第二步的操作，直到p等于（1）中的初始点（横坐标最小的点）。

（4）第二步中找到点q后，可能存在点r，位于向量pq中的某一点，这个时候点r也是凸包上的点，应该加上这样的点。

（5）叉积（外积，向量积）的模，以及叉积的计算公式，如下所示。

\[| \ \vec{a} \times \vec{b} \ | = | \ \vec{a} \ | \cdot | \ \vec{b} \ | \cdot \sin \theta
\]

\[\vec{a} \times \vec{b} = det\begin{vmatrix}
i & j & k\\
a_x & a_y & a_z\\
b_x & b_y & b_z
\end{vmatrix}, i = (1,0,0), j = (0,1,0), k = (0,0,1)
\]

对于二维向量，\(a_z, b_z\)都为0，可以得到叉积模的计算方式为\(a_x * b_y - a_y * b_x\)，这个值小于0则表示a转向b（转向角度在0到180度以内）的方向为顺时针。其实这个符号就是sin的符号，决定着叉积的方向，根据右手螺旋法则，四指为向量的旋转方向，大拇指为叉积的方向，四指逆时针时，大拇指方向为正，即sin符号为正。

时间复杂度O(nH)，空间复杂度O(n)，H表示凸包上的点的个数

class Solution(object):
    def cross_product_norm(self, p, q, r):
        return (q.x - p.x) * (r.y - q.y) - (q.y - p.y) * (r.x - q.x)

    def between(self, p, q, r):
        a = q.x >= p.x and q.x <= r.x or q.x >= r.x and q.x <= p.x
        b = q.y >= p.y and q.y <= r.y or q.y >= r.y and q.y <= p.y
        return a and b

    def outerTrees(self, points):
        """
        :type points: List[Point]
        :rtype: List[Point]
        """
        n = len(points)
        if n < 4:
            return points
        left_most = 0
        convex_index = [0] * n
        for i in range(n):
            if points[i].x < points[left_most].x:
                left_most = i
        p = left_most
        while True:
            q = (p+1)%n
            for r in range(n):
                if(self.cross_product_norm(points[p], points[q], points[r])<0):
                    q = r

            for r in range(n):
                if(r != p and r != q and self.cross_product_norm(points[p], points[q], points[r]) == 0 and self.between(points[p], points[r], points[q])):
                    convex_index[r] = 1
            convex_index[q] = 1
            p = q
            if (p == left_most):
                break
        return [points[i] for i in range(n) if convex_index[i]]

4. Graham扫描法

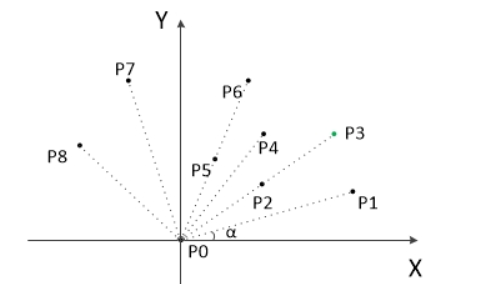
（1）纵坐标最小的点一定是凸包上的点，记为P0，以P0为原点，计算各个点相对于P0的幅角，从小到大排序，幅角相同时，距离近的排在前面。

（2）如下图所示（图源见参考资料），此时第一个点P1和最后一个点P8一定是凸包上的点。先将P0和P1放入栈中，然后以P2作为“当前点”开始扫描，重复以下的扫描策略，直到遇到P8时停止。

（3）扫描策略：连接栈顶的下一个点和栈顶的点构成向量（初始时连接的是P0和P1）。

如果“当前点”在向量的左边，把当前点压栈，然后“当前点”变成下一个点。

如果“当前点”在向量的右边，出栈栈顶元素。

（4）以下图所示，对算法举个例子。

连接P0和P1，发现P2在左侧，P2入栈。

连接P1和P2，发现P3在右侧，P2出栈。

连接P0和P1，发现P3在左侧，P3入栈。

连接P1和P3，发现P4在左侧，P4入栈。

连接P3和P4，发现P5在左侧，P5入栈。

连接P4和P5，发现P6在右侧，P5出栈。

连接P3和P4，发现P6在右侧，P4出栈。

连接P1和P3，发现P6在左侧，P6入栈。

连接P3和P6，发现P7在左侧，P7入栈。

连接P6和P7，发现P8在左侧，P8入栈。

遇到最后一个点P8，终止迭代。

（5）如果P0P8向量中间还有一个点，比如有个P75，那么这个P75会在P8之前被出栈，而这个点也是凸包上的点，所以要把最后一条射线上共线的那些点也加入凸包中。

时间复杂度O(N*logN)，空间复杂度O(N)

class Solution(object):
    def cross_product_norm(self, p, q, r):
        return (q.x - p.x) * (r.y - q.y) - (q.y - p.y) * (r.x - q.x)

    def cos_square(self, p0, p):
        x_value = p.x - p0.x
        y_value = p.y - p0.y
        cos_value = x_value * x_value * 1.0 / (x_value * x_value + y_value * y_value)
        if x_value < 0:
            cos_value = - cos_value
        return cos_value

    def norm(self, p0, p):
        x_value = p.x - p0.x
        y_value = p.y - p0.y
        return x_value * x_value + y_value * y_value

    def outerTrees(self, points):
        """
        :type points: List[Point]
        :rtype: List[Point]
        """
        n = len(points)
        if n < 4:
            return points
        bottom_most = 0
        for i in range(n):
            if points[i].y < points[bottom_most].y:
                bottom_most = i
        p0 = points[bottom_most]
        del points[bottom_most]
        n -= 1
        points.sort(key = lambda p: (- self.cos_square(p0, p), self.norm(p0, p)))

        stack_points = []
        stack_points.append(p0)
        stack_points.append(points[0])

        i = 1
        while True:
            if(self.cross_product_norm(stack_points[-2], stack_points[-1], points[i]) >= 0):
                stack_points.append(points[i])
                i += 1
            else:
                stack_points.pop()
            if(i == n):
                for j in range(n-1)[::-1]:
                    if(self.cross_product_norm(p0, points[n-1], points[j]) == 0):
                        stack_points.append(points[j])
                    else:
                        break
                break
        return stack_points

参考资料

凸包问题的五种解法-csdn