树的直径【p3629】[APIO2010]巡逻

Description

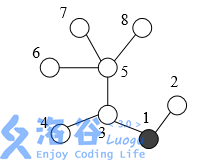
在一个地区中有 n 个村庄，编号为 1, 2, ..., n。有 n – 1 条道路连接着这些村 庄，每条道路刚好连接两个村庄，从任何一个村庄，都可以通过这些道路到达其 他任一个村庄。每条道路的长度均为 1 个单位。 为保证该地区的安全，巡警车每天要到所有的道路上巡逻。警察局设在编号 为 1 的村庄里，每天巡警车总是从警察局出发，最终又回到警察局。 下图表示一个有 8 个村庄的地区，其中村庄用圆表示（其中村庄 1 用黑色的 圆表示），道路是连接这些圆的线段。为了遍历所有的道路，巡警车需要走的距 离为 14 个单位，每条道路都需要经过两次。

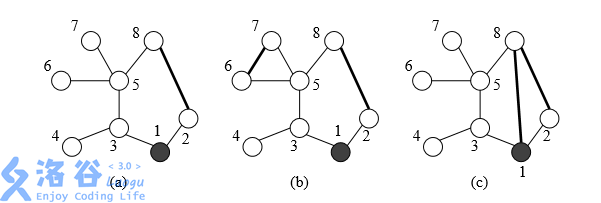
为了减少总的巡逻距离，该地区准备在这些村庄之间建立 K 条新的道路， 每条新道路可以连接任意两个村庄。两条新道路可以在同一个村庄会合或结束 （见下面的图例（c））。 一条新道路甚至可以是一个环，即，其两端连接到同一 个村庄。 由于资金有限，K 只能是 1 或 2。同时，为了不浪费资金，每天巡警车必须 经过新建的道路正好一次。 下图给出了一些建立新道路的例子：

在(a)中，新建了一条道路，总的距离是 11。在(b)中，新建了两条道路，总 的巡逻距离是 10。在(c)中，新建了两条道路，但由于巡警车要经过每条新道路 正好一次，总的距离变为了 15。 试编写一个程序，读取村庄间道路的信息和需要新建的道路数，计算出最佳 的新建道路的方案使得总的巡逻距离最小，并输出这个最小的巡逻距离。

Input

第一行包含两个整数 n, K(1 ≤ K ≤ 2)。接下来 n – 1 行，每行两个整数 a, b， 表示村庄 a 与 b 之间有一条道路(1 ≤ a, b ≤ n)。

Output

输出一个整数，表示新建了 K 条道路后能达到的最小巡逻距离。

很明显,新建的边要在树上最长的链(树的直径)上建.构成一个最大的环.这样能使我们走过这些在直径上的边对答案的影响最小.

如果建两条边,同理,第二条边要建在次长链上,

问题难在如何求出次长链.

我们只需要将直径上的边的边权全部标成\(-1\)就好了.

这样就对这些边对答案的贡献就可以抵消了,就达到了不选的效果.

这里用\(dfs\)求了树的直径,又用树形\(Dp\)求了新的直径.

应该不是很难理解.

代码

#include<cstdio>
#include<cctype>
#include<iostream>
#define N 100008
#define  R register
using namespace std;
inline void in(int &x)
{
	int f=1;x=0;char s=getchar();
	while(!isdigit(s)){if(s=='-')f=-1;s=getchar();}
	while(isdigit(s)){x=x*10+s-'0';s=getchar();}
	x*=f;
}
int n,k,head[N],tot=1,pos,dis[N]={-1},root,mx,pre[N],mxx;
struct cod{int u,v,w;}edge[N<<2];
int dist[N];
bool vis[N];
inline void add(int x,int y)
{
	edge[++tot].u=head[x];
	edge[tot].v=y;
	edge[tot].w=1;
	head[x]=tot;
}
void dfs(int u,int fa)
{
	dis[u]=dis[fa]+1;
	for(R int i=head[u];i;i=edge[i].u)
	{
		if(edge[i].v==fa)continue;
		dfs(edge[i].v,u);
		pre[edge[i].v]=i;
	}
}
void dp(int x)
{
	vis[x]=true;
	for(R int i=head[x];i;i=edge[i].u)
	{
		if(vis[edge[i].v])continue;
		dp(edge[i].v);
		mxx=max(mxx,dist[x]+dist[edge[i].v]+edge[i].w);
		dist[x]=max(dist[x],dist[edge[i].v]+edge[i].w);
	}
}
int main()
{
	in(n);in(k);
	for(R int i=1,x,y;i<n;i++)
		in(x),in(y),add(x,y),add(y,x);
	dfs(1,0);
	for(R int i=1;i<=n;i++)root=dis[i]>dis[root]?i:root;
	for(R int i=1;i<=n;i++)dis[i]=pre[i]=0;
	dfs(root,0);
	for(R int i=1;i<=n;i++)
		if(dis[i]>mx)
		{
			mx=dis[i];
			pos=i;
		}
	if(k==1)
	{
		printf("%d",2*(n-1)+1-mx);
		return 0;
	}
	for(R int i=pre[pos];i;i=pre[edge[i^1].v])
		edge[i].w=edge[i^1].w=-1;
	dp(root);
	printf("%d",2*(n-1)+2-mx-mxx);
}