node安装启动服务

一、下载安装包: 
node下载地址：https://nodejs.org/en/download/，根据自己电脑的配置下载相应的windows64位安装包，下载完成后，进行安装。下面我用的8.9.0版本安装

git下载地址：https://git-scm.com/downloads，根据自己电脑的配置下载相应的windows64位安装包，下载完成后，进行安装。

二、开始安装

下载完成后，双击“node-v8.9.0-x64，开始安装Node.js。

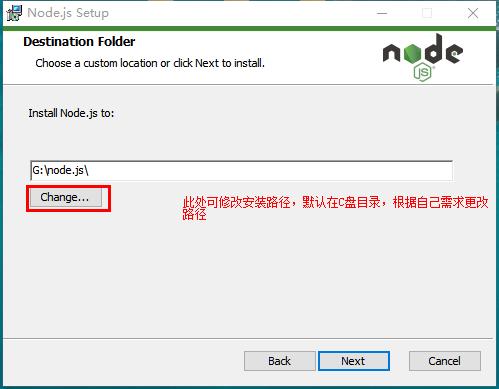
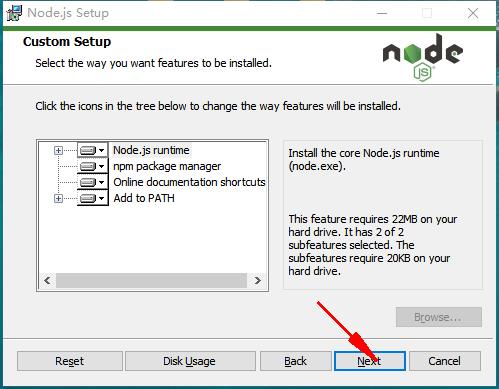
三、检查是否安装成功

安装完成后，进入安装路径的node.js文件内右键选择'Git Bash Here'打开命令行窗口，检查是否安装成功，如下图所示，输入node -v出现node.js的版本，输入npm -v出现npm的版本，说明两者均已安装成功。

四、配置环境变量 
说明：这里的环境配置主要配置的是npm安装的全局模块所在的路径，以及缓存cache的路径，之所以要配置，是因为以后在执行类似：npm install express [-g] （后面的可选参数-g，g代表global全局安装的意思）的安装语句时，会将安装的模块安装到【C:\Users\用户名\AppData\Roaming\npm】路径中，占C盘空间。
例如：我希望将全模块所在路径和缓存路径放在我node.js安装的文件夹中，则在我安装的文件夹【D:\Develop\nodejs】下创建两个文件夹【node_global】及【node_cache】：

创建完两个空文件夹之后，打开cmd命令窗口，输入

npm config set prefix "G:\nodejs\node_global"
npm config set cache "G:\nodejs\node_cache" 

 

接下来设置环境变量，关闭git窗口，“我的电脑”-右键-“属性”-“高级系统设置”-“高级”-“环境变量”

进入环境变量对话框，在【系统变量】下新建【NODE_PATH】，输入【G:\node.js\node_global】，将【用户变量】下的【Path】修改为【G:\node.js\node_global】

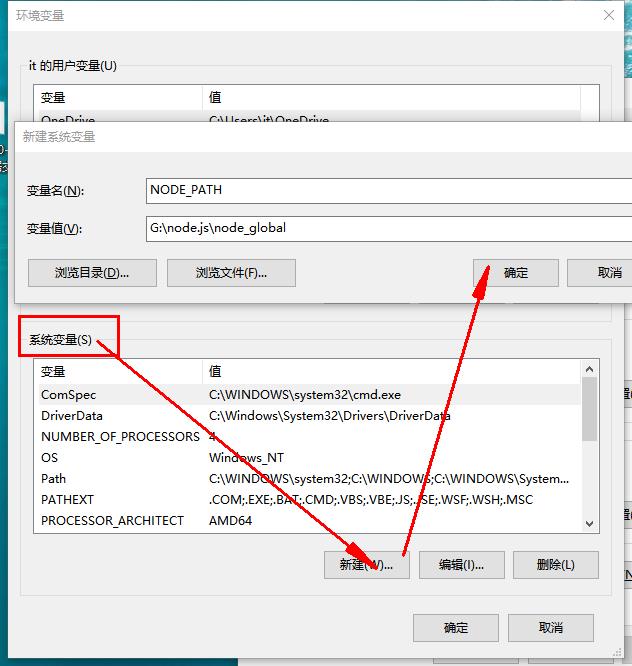
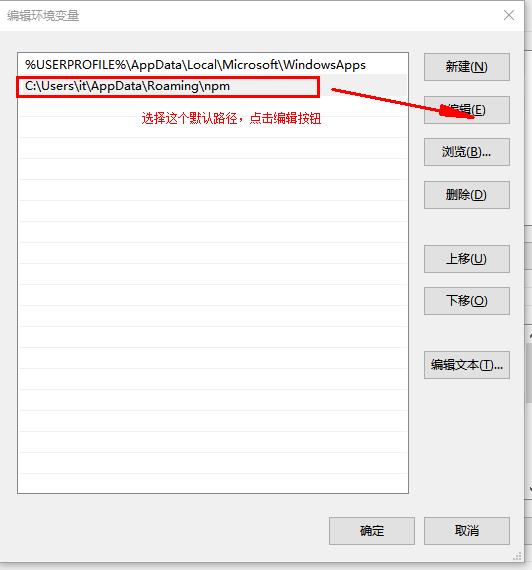
五、选择cnpm

1、说明：因为npm安装插件是从国外服务器下载，受网络影响大，可能出现异常，如果npm的服务器在中国就好了，所以我们乐于分享的淘宝团队干了这事。！来自官网：“这是一个完整 npmjs.org 镜像，你可以用此代替官方版本(只读)，同步频率目前为 10分钟 一次以保证尽量与官方服务同步。”；

2、官方网址：http://npm.taobao.org；

3、安装：命令提示符执行npm install cnpm -g 

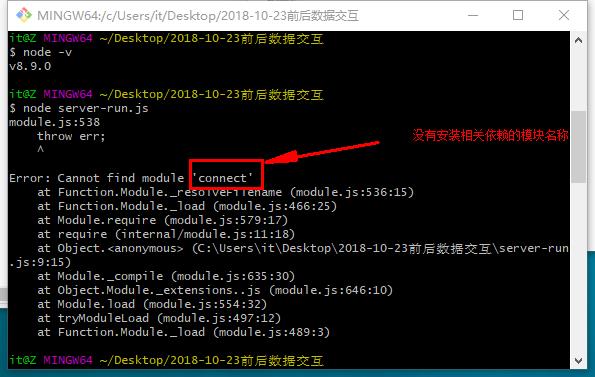
上图安装相关依赖：cnpm install connect

备注：node常用命令：

pwd //显示当前工作目录
cd  <name>  //切换文件夹
cd ..      //返回上一级目录
cls       //清空当前控制台
mkdir <name> //创建文件夹
ls        //显示当前目录所有数据
rm <name> //删除文件

npm -v   //查看npm版本
node -v //查看node版本
node  *.js //执行js文件
node     //进入命令交互模式

sudo npm install npm -g //升级npm
npm install <Module Name> //安装模块
npm uninstall <Module Name>//卸载模块

npm install nodemon -g //安装nodemon
nodemon *.js //执行js文件并且进行监视，文件变化了会重新执行文件

六、启动服务

按‘ctrl+c’关闭服务，不然启用多个服务，会出现端口占用问题