hdu1198--并查集

Problem Description

Benny has a spacious farm land to irrigate. The farm land is a rectangle, and is divided into a lot of samll squares. Water pipes are placed in these squares. Different square has a different type of pipe. There are 11 types of pipes, which is marked from A to K, as Figure 1 shows.

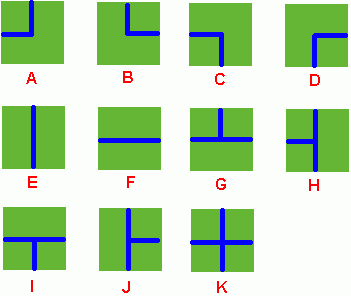
Figure 1

Benny has a map of his farm, which is an array of marks denoting the distribution of water pipes over the whole farm. For example, if he has a map

ADC

FJK

IHE

then the water pipes are distributed like

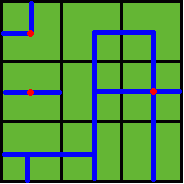
Figure 2

Several wellsprings are found in the center of some squares, so water can flow along the pipes from one square to another. If water flow crosses one square, the whole farm land in this square is irrigated and will have a good harvest in autumn.

Now Benny wants to know at least how many wellsprings should be found to have the whole farm land irrigated. Can you help him?

Note: In the above example, at least 3 wellsprings are needed, as those red points in Figure 2 show.

 

Input

There are several test cases! In each test case, the first line contains 2 integers M and N, then M lines follow. In each of these lines, there are N characters, in the range of 'A' to 'K', denoting the type of water pipe over the corresponding square. A negative M or N denotes the end of input, else you can assume 1 <= M, N <= 50.

 

Output

For each test case, output in one line the least number of wellsprings needed.

 

Sample Input

2 2
DK
HF

3 3
ADC
FJK
IHE

-1 -1

 

Sample Output

2
3

 

解题思路：按行对每个节点map(i,j)，找到其下方及右方的水管类型，判断其是否能与map(i,j)相连。在这题中只需要判断两个方向而不是四方方向。如下

1 2 3

4 5 6

从1判断2节点是否与1能够相连;若相连则把1和2放入到同一个集合类中，当下次从2搜索时，由于1和2已经在一个集合类中，所以不需要对1进行搜索;如果1和2无法连在一起，那么从2搜到1也是无法相连的。所以只需要搜索节点下方和右方的区域。

从上面给出的类型可以看出，遇到A,B,F,G这四种类型的水管时，不用搜索其下方的区域，因为无论其下方是什么类型都不可能与这四种水管相连。同样若是A,C,E,H这样的类型时也不需要考虑其右边的情况。

当前区域要想与下方的区域连在一起，则下方的水管类型只能下面的类型A,B,E,G,H,J,K。则样若与右方区域相连，右方区域的类型为A,C,F,G,H,I,K

#include<stdio.h>
#include<string.h>
//
char str[2][9]={{"ABEGHJK"},{"ACFGHIK"}};
int f[2505],m,n;
char map[52][52];

int check(int x,int y)
{
	if(x>=0 && x<m && y>=0 && y<n)return 1;
	return 0;
}

int getFather(int a)
{
	while(a!=f[a])a=f[a];
	return a;
}
/** 合并两个集合 */
void Union(int a,int b)
{
	int root1=getFather(a);
	int root2=getFather(b);
	if(root1!=root2)
	{
		if(root1<root2)f[root2]=root1;
		else f[root1]=root2;
	}
}
/**
* 判断两个型号的水管是否可以连在一起
*/
int judge(char c,int flag)
{
	int i;
	for(i=0;i<7;i++)
	{
		if(str[flag][i]==c)return i+1;
	}
	return 0;
}
void process()
{
	int i,j,dx,dy;
	char c;
	for(i=0;i<=n*m;i++)f[i]=i;
	for(i=0;i<m;i++)
	{
		for(j=0;j<n;j++)
		{

			c=map[i][j];
			//判断下方，当前区域的类型是除A,B,F,G以外的。
			if(c=='C' || c=='D' || c=='E' || c=='H'
				|| c=='I' || c=='J' || c=='K')
			{
				dx = i+1;
				dy = j;
				if(check(dx,dy))
				{
					//下方区域是否是 A,B,E,G,H,J,K之一
					if(judge(map[dx][dy],0))
					{
						//合并两个区域
						Union(i*n+j,dx*n+dy);
					}
				}
			}
			//判断右方
			if(c=='B' || c=='D' || c=='F' || c=='G'
				|| c=='I' || c=='J' || c=='K')
			{
				dx=i;
				dy=j+1;
				if(check(dx,dy))
				{
					//右方区域是否是A,C,F,G,H,I,K之一
					if(judge(map[dx][dy],1))
					{
						Union(i*n+j,dx*n+dy);
					}
				}
			}
		}
	}
	int result=0;
	for(i=0;i<n*m;i++)if(f[i]==i)result++;
	printf("%d\n",result);
}
int main()
{
	int i;
	while(scanf("%d%d",&m,&n))
	{
		if(m<0 || n<0)break;
		for(i=0;i<m;i++)scanf("%s",map[i]);
		process();
	}
	return 0;
}